Апейрогон
Апейрогон або нескінченнокутник (від дав.-гр. ἄπειρος — нескінченний або безмежний і дав.-гр. γωνία — кут) — узагальнення многокутника зі зліченно-нескінченним числом сторін[1].
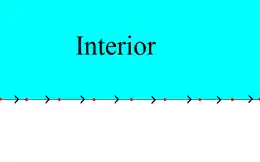
Правильний апейрогон
Правильний апейрогон має сторони рівної довжини, як і будь-який інший правильний многокутник. Його символ Шлефлі — {∞}, діаграма Коксетера — Динкіна — ![]()
![]()
![]() .
.
Правильний апейрогон розбиває площину на дві півплощини, утворюючи апейрогональний діедр {∞,2}. Внутрішню частину апейрогона можна визначити, вказавши напрям сторін.
| Правильні | Однорідні | ||
|---|---|---|---|
| ∞.∞ | 2∞ | 4.4.∞ | 3.3.3.∞ |
 |
 |
 |
 |
| {∞, 2} |
{2, ∞} |
t{2, ∞} |
sr{2, ∞} |
Правильними апейрогонами можна вважати прямі, що складаються з ребер чотирьох однорідних мозаїк і п'яти мозаїк, двоїстих однорідним, на евклідовій площини.
| 3 напрямки | 1 напрямок | 2 напрямки | |
|---|---|---|---|
 Шеститрикутна мозаїка |
 Трикутний паркет |
 Подовжена трикутна мозаїка |
 Квадратний паркет (кадриль) |
| 3 напрямки | 6 напрямків | 1 напрямок | 4 напрямку | |
|---|---|---|---|---|
 Тетрамозаїка |
 Розділена трикутна мозаїка |
 Розділена шестикутна мозаїка |
 Призматична п'ятикутна мозаїка |
 Розділена квадратна мозаїка |
Неправильні апейрогони
Ізогональний апейрогон має вершини одного типу і сторони двох типів (довжин), що чергуються.
Квазіправильний апейрогон — ізогональний апейрогон з однаковими довжинами сторін.
Ізотоксальний апейрогон є двоїстим відносно ізогонального. Він має один тип ребер і два типи вершин і геометрично ідентичний правильному апейрогону, що можна показати почерговим розфарбуванням вершин у два кольори.
| Правильний | … |
|---|---|
| Квазіправильний | … |
| Ізогональний | … |
| Ізотоксальний | … |
Апейрогони на гіперболічній площині
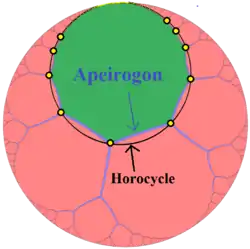
Правильні апейрогони на гіперболічній площині мають кривину, так само, як і многокутники зі скінченним числом сторін. Навколо апейрогона на гіперболічній площині можна описати орицикл або еквідистанту (гіперцикл), аналогічно тому, як навколо многокутника зі скінченним числом сторін можна описати коло.
![]()
![]()
![]()
![]()
![]()
| 3 | 4 | 5 |
|---|---|---|
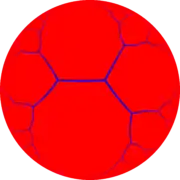 {∞,3} |  {∞,4} | 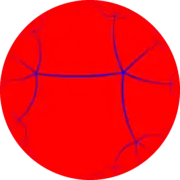 {∞,5} |
![]()
![]()
![]()
![]()
![]()
| 6 | 7 | 8 | … | ∞ |
|---|---|---|---|---|
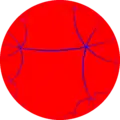 {∞,6} |  {∞,7} |  {∞,8} |  {∞,∞} | |
| {∞, 3} | tr{∞, 3} | tr{12i, 3} |
|---|---|---|
 Правильний: {∞} |
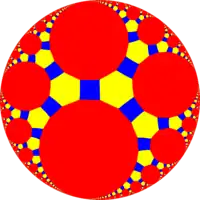 Квазіправильний: t{∞} |
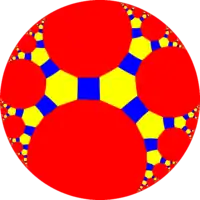 Квазіправильний: t{12i} |
Примітки
- >Coxeter, Regular polytopes, p.45
Література
- H. S. M. Coxeter. Regular Polytopes. — 3rd. — New York : Dover Publications, 1973. — С. 121–122. — ISBN 0-486-61480-8.
- Grünbaum, B. Regular polyhedra — old and new, Aequationes Math. 16 (1977) p. 1-20
- Coxeter, H. S. M. and Moser, W. O. J. Generators and Relations for Discrete Groups. — New York : Springer-Verlag, 1980. — ISBN 0-387-09212-9. (1st ed, 1957) 5.2 The Petrie polygon {p, q}.