Осоедр
n -кутний осоедр — мозаїка з двокутників на сферичній поверхні така, що кожен з двокутників має дві спільні вершини (протилежні точки сфери) з іншими двокутниками.

Правильний n-кутний осоедр має символ Шлефлі {2, n}, а кожен двокутник має внутрішній кут 2π/n радіан (360/n градусів)[1] [2].
Осоедри як правильні багатогранники
Для правильних багатогранників, символ Шлефлі яких дорівнює {m, n}, число багатокутних граней можна знайти за формулою:
Правильні багатогранники, відомі з античних часів, є єдиними багатогранниками, що дають у результаті ділення ціле число для m ≥ 3 і n ≥ 3. Обмеження m ≥ 3 призводить до того, що багатокутні грані повинні мати щонайменше три сторони.
Якщо розглядати багатогранники як сферичну мозаїку, це обмеження можна ослабити, оскільки двокутники можна розглядати як сферичні двокутні фігури, що мають ненульову площу. Допущення m = 2 породжує новий нескінченний клас правильних багатогранників, тобто осоедрів.
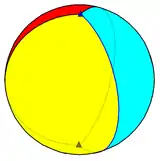 Правильний трикутний осоедр, {2,3}, поданий у вигляді мозаїки з трьох двокутників на сфері. |
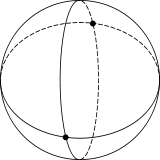 Правильний чотирикутний осоедр, поданий у вигляді мозаїки з чотирьох двокутників на сфері. |
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Малюнок |  |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| Шлефлі | {2,2} | {2,3} | {2,4} | {2,5} | {2,6} | {2,7} | {2,8} | {2,9} | {2,10} | {2,11} | {2,12} | |
| Коксетер | ||||||||||||
| Граней і ребер |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Вершин | 2 | |||||||||||
Калейдоскопічна симетрія
Двокутні грані 2n-осоедра, {2,2 n}, представляють фундаментальні області діедральної симетрії: Cnv, [n], (*nn), порядок 2n. Області дзеркального відбиття можна показати, використовуючи почергове розмальовування двокутників. Розсічення двокутників на два сферичних трикутники утворюють біпіраміди і визначають діедричну симетрію Dnh, порядок 4n.
| Симетрія | C1v | C2v | C3v | C4v | C5v | C6v |
|---|---|---|---|---|---|---|
| Осоедр | {2,2} | {2,4} | {2,6} | {2,8} | {2,10} | {2,12} |
| Фундаментальні області |  |
 |
 |
 |
 |
 |
Зв'язок з тілами Штейнмеца
Чотирикутний осоедр топологічно еквівалентний біциліндру, тобто, перетину двох циліндрів під прямим кутом.
Похідні багатогранники
Двоїстим багатогранником n-кутного осоедра {2, n} є n-кутний діедр, {n, 2}. Багатогранник {2,2} самодвоїстий і є одночасно осоедром і діедром.
Осоедр можна модифікувати тим же способом, що й інші багатогранники, породжуючи зрізані варіанти. Зрізаний n-кутний осоедр — це n-кутна призма.
Нескінченнокутний осоедр
В границі осоедр стає нескінченнокутним і являє собою двовимірне замощення:
Осотопи
Багатовимірні аналоги, в загальному випадку називаються осотопами. Правильний осотоп із символом Шлефлі {2,p,…,q} має дві вершини і в обох вершинах вершинною фігурою є {p,…,q}.
Двовимірний осотоп (багатокутник) {2} — це двокутник.
Етимологія
Термін «осоедр» (hosohedron) запропонував Г. С. М. Коксетер і, можливо, вивівши його від грецького ὅσος (осос) «скільки завгодно», що вказує на можливість осоедра мати «як завгодно багато граней»[3].
Див. також
Примітки
- Coxeter, 1973, с. 12.
- McMullen & Schulte, 2002, с. 161.
- Schwartzman, 1994, с. 108–109.
Література
- Coxeter H. S. M. . Regular Polytopes. — New York : Dover Publications Inc, 1973. — ISBN 0-486-61480-8.
- McMullen, Peter; Schulte, Egon. . Abstract Regular Polytopes. 1st edition. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
- Schwartzman, Steven. . The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. — MAA, 1994. — ISBN 978-0-88385-511-9.
