Конфігурація вершини

В геометрії конфігурація вершини[1][2][3] — це скорочене позначення для подання вершинної фігури, багатогранника або мозаїки у вигляді послідовності граней навколо вершини. Для однорідного багатогранника існує тільки один тип вершин, а тому конфігурація вершини повністю визначає багатогранник. (Хіральні багатогранники існують у вигляді дзеркальних пар з однаковою конфігурацією вершин.)





Ікосододекаедр



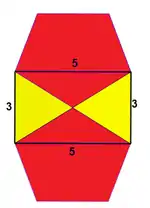Вершинна фігура,
подана як
3.5.3.5 або (3.5)2

Конфігурація вершини визначається як послідовність чисел, що представляють число сторін граней, які оточують вершину. Позначення «a.b.c» позначає вершину з трьома гранями біля неї і ці грані мають a, b і c сторін (ребер).

Наприклад, «3.5.3.5» позначає вершину, що належить чотирьом граням, почергово трикутникам і п'ятикутникам. Ця конфігурація вершини визначає вершинно транзитивний ікосододекаедр. Позначення циклічне, так що початкова точка значення не має. Таким чином, 3.5.3.5 — це те ж саме, що і 5.3.5.3. Порядок важливий, так що 3.3.5.5 — це не те ж саме, що 3.5.3.5. (У першому випадку за двома поруч розташованими трикутниками слідують два п'ятикутники.) Повторювані елементи можуть бути скорочені зазначенням верхнього індексу, так що наш приклад можна записати у вигляді (3.5)2.

Поряд з терміном конфігурація вершини в різних джерелах використовують також терміни vertex description (опис вершини)[4][5][6], vertex type (тип вершини)[7][8], vertex symbol (символ вершини)[9][10], vertex arrangement (компонування вершини)[11], vertex pattern (шаблон вершини)[7], face-vector (вектор межі)[12]. Для конфігурації вершини використовується, крім того, термін символ Канді і Роллетта, оскільки вони використовували конфігурацію вершини для опису архімедових тіл у книзі 1952 року Mathematical Models (Математичні моделі)[13][14][15][16].

Вершинні фігури

Конфігурація вершини може бути подана як вершинна фігура з багатокутників, що показує грані навколо вершини. Ця вершинна фігура має 3-вимірну структуру, оскільки грані не знаходяться в одній площині, але для вершинно однорідних багатогранників всі сусідні вершини знаходяться в одній площині, так що можна використовувати для візуального подання конфігурації вершини ортогональну проекцію.

Варіанти і використання
Регулярні сітки вершинних фігур, {p, q} = pq

{3,3} = 33
Дефект 180°
{3,4} = 34
Дефект 120°
{3,5} = 35
Дефект 60°
{3,6}=36Дефект 0°

{4,3}
Дефект 90°
{4,4}=44Дефект 0°
{5,3} = 53
Дефект 36°
{6,3}=

63Дефект 0°

У вершині має бути щонайменше 3 грані і вершина має кутовий дефект.
Кутовий дефект 0° дає можливість покрити площину правильною мозаїкою.
За теоремою Декарта число вершин дорівнює 720°/дефект (4π радіан/дефект).

Використовується різний вигляд запису, іноді через кому (,) іноді через крапку (.). Може також використовуватися верхній індекс. Наприклад, 3.5.3.5 іноді записується у вигляді (3.5)2.

Позначення може розглядатися як розгорнута форма символу Шлефлі для правильних багатогранників. Позначення Шлефлі {p, q} означає q p-кутників навколо кожної вершини. Так що {p, q} можна записати p.p.p... (q разів) або pq. Наприклад, у ікосаедра {3,5} = 3.3.3.3.3 або 35.

Цей запис застосовний як до багатокутних мозаїк, так і до багатогранників. Плоска конфігурація вершини означає однорідну мозаїку так само, як неплоска конфігурація вершини означає однорідний багатогранник.

Позначення не однозначне для хіральних видів. Наприклад, плосконосий куб має форми, ідентичні при дзеркальному відображенні. Обидві форми мають конфігурацію вершини 3.3.3.3.4.

Зірчасті багатокутники

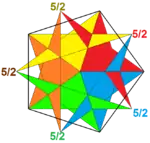
Позначення застосовується також до неопуклих правильних граней, зірчастих багатокутників. Наприклад, пентаграма має символ {5/2}, що означає, що багатокутник має 5 сторін, які обходять центр два рази.

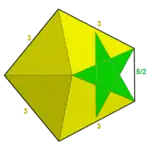
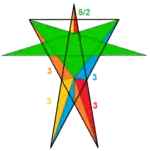
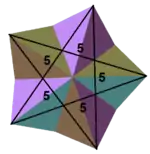
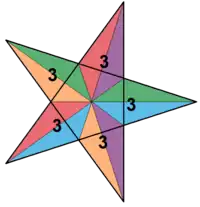
Наприклад, існує 4 правильні зірчасті багатогранники з правильними багатокутниками або зірчастими вершинними фігурами. Малий зірчастий додекаедр має символ Шлефлі {5/2,5}, який розгортається в явну конфігурацію вершини 5/2.5/2.5/2.5/2.5/2, що можна подати у вигляді (5/2)5. Великий зірчастий додекаедр з символом {5/2,3} має трикутну вершинну фігуру і конфігурацію (5/2.5/2.5/2) або (5/2)3. Великий додекаедр з символом {5,5/2} має пентаграмну вершинну фігуру з конфігурацією вершини (5.5.5.5.5)/2 або (55)/2. Великий ікосаедр з символом {3,5/2} також має пентаграмну вершинну фігуру з конфігурацією вершини (3.3.3.3.3)/2 або (35)/2.

{5/2,5} = (5/2)5 {5/2,3}= (5/2)3 34.5/2 34.5/3 (34.5/2)/2
{5,5/2} = (55)/2 {3,5/2} = (35)/2 V.34.5/2 V34.5/3 V(34.5/2)/2

Всі однорідні конфігурації вершин правильних опуклих багатокутників

Напівправильні багатогранники мають конфігурацію вершин з додатним кутовим дефектом.

Примітка: Вершинна фігура може представляти правильну або напівправильну мозаїку на площині, якщо її дефект дорівнює нулю. Вершинна фігура може представляти мозаїку на гіперболічній площині, якщо її дефект від'ємний.

Для однорідних багатогранників кутовий дефект можна використовувати для обчислення числа вершин. Теорема Декарта стверджує, що сума всіх кутових дефектів на топологічній сфері повинна дорівнювати 4π радіан або 720°.

Оскільки в однорідного багатогранника всі вершини ідентичні, це відношення дозволяє нам розрахувати число вершин, яке дорівнює частці 4π/дефект або 720°/дефект.

Приклад: зрізаний куб 3.8.8 має кутовий дефект 30°. Таким чином, багатогранник має 720/30 = 24 вершин.

Зокрема, звідси випливає, що {a,b} має 4 / (2 - b(1 - 2/a)) вершин.

Будь-яка числова конфігурація вершини потенційно однозначно визначає напівправильний багатогранник. Однак не всі конфігурації можливі.

Топологічні вимоги обмежують існування багатогранника. Зокрема, p.q.r означає, що p-кутник оточений поперемінно q-кутниками і r-кутниками, так що або p парне, або q дорівнює r. Так само q парно, або p дорівнює r, r парно, або p дорівнює q. Таким чином, потенційно можливими трійками будуть 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4.n (для будь-якого n>2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. Фактично всі ці конфігурації з трьома гранями, що зустрічаються в одній вершині, існують.

Так само, коли чотири грані зустрічаються в одній вершині, p.q.r.s, якщо одне з чисел непарне, інші повинні бути рівними.

Число в дужках — це число вершин, обчислене за кутовим дефектом.

Трійки

  • правильні тіла 3.3.3 (4), 4.4.4 (8), 5.5.5 (20)
  • призми 3.4.4 (6), 4.4.4 (8; перелічена також вище), 4.4.n (2n)
  • архімедові тіла 3.6.6 (12), 3.8.8 (24), 3.10.10 (60), 4.6.6 (24), 4.6.8 (48), 4.6.10 (120), 5.6.6 (60).
  • правильна мозаїка 6.6.6
  • напівправильні мозаїки 3.12.12, 4.6.12, 4.8.8

Четвірки

  • правильне тіло 3.3.3.3 (6)
  • антипризмы 3.3.3.3 (6; перелічена також вище), 3.3.3.n (2n)
  • архімедові тіла 3.4.3.4 (12), 3.5.3.5 (30), 3.4.4.4 (24), 3.4.5.4 (60)
  • правильна мозаїка 4.4.4.4
  • напівправильні мозаїки 3.6.3.6, 3.4.6.4

П'ятірки

  • правильне тіло 3.3.3.3.3 (12)
  • архімедові тіла 3.3.3.3.4 (24), 3.3.3.3.5 (60) (обидва хіральні)
  • напівправильні мозаїки 3.3.3.3.6[en] (хіральні), 3.3.3.4.4, 3.3.4.3.4 (зауважте, що два різні порядки тих самих чисел дають різні мозаїки)

Шістки

Конфігурація грані
Ромбододекаедр

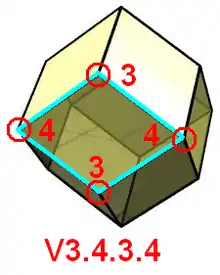
Двоїсті однорідним многогранникам, каталанові тіла, включно з біпірамідами і трапецоедрами, є вертикально правильними (транзитивними за гранями, а тому можуть бути ідентифіковані подібною нотацією, яку іноді називають конфігурацією грані[2]. Канді і Роллетт (Cundy, Rollett) ставлять перед цими подвійними позначеннями символ V. А в книзі Tilings and Patterns[17] для ізоедральних мозаїк використовуються квадратні дужки.

Це позначення представляє послідовне число граней біля кожної вершини навколо грані[18]. Наприклад, V3.4.3.4 або V(3.4)2 представляють ромбододекаедр, який транзитивний за гранями — будь-яка межа є ромбом, а вершини ромба, що чергуються, оточують 3 або 4 грані.

Примітки
  1. The Uniform Polyhedra Roman E. Maeder (1995)
  2. Steurer, Deloudi, 2009, с. 18-20, 51-53.
  3. Laughlin, 2014, с. 16-20.
  4. Archimedean Polyhedra Архівовано 5 липня 2017 у Wayback Machine. Steven Dutch
  5. Uniform Polyhedra Jim McNeill
  6. Uniform Polyhedra and their Duals Robert Webb
  7. Kovič, 2011, с. 491-507.
  8. 3. General Theorems: Regular and Semi-Regular Tilings Kevin Mitchell, 1995
  9. Resources for Teaching Discrete Mathematics: Classroom Projects, History, modules, and articles, edited by Brian Hopkins
  10. Vertex Symbol Robert Whittaker
  11. Hann, 2012.
  12. Deza, Shtogrin, 2000, с. 807-814.
  13. Weisstein, Eric W. {{{title}}}(англ.) на сайті Wolfram MathWorld.
  14. Popko, 2012, с. 164.
  15. Laughlin, 2014, с. 16.
  16. Weisstein, 1999.
  17. Grünbaum, Shephard, 1987.
  18. Cundy, Rollett, 1952.

Література
  • Walter Steurer, Sofia Deloudi. Crystallography of Quasicrystals: Concepts, Methods and Structures. — Springer, 2009. — Т. 126. — (Springer series in materials science). — ISBN 978-3-642-01898-5.
  • Michel Deza, Mikhail Shtogrin. Uniform Partitions of 3-space, their Relatives and Embedding // Europ. J. Combinatorics. — 2000. — Вип. 21.
  • Physical Metallurgy / David E. Laughlin, Kazuhiro Hono. — 5. — Elsevier, 2014. — Т. 1. — ISBN 978-0-444-59598-0.
  • Edvard S. Popko. Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. — CRC Press, 2012. — ISBN 978-1-4665-0430-1.
  • Jurij Kovič. Symmetry-type graphs of Platonic and Archimedean solids // MATHEMATICAL COMMUNICATIONS. — 2011. — Вип. 16. — С. 491-507.
  • Eric W. Weisstein. The CRC concise encyclopedia of mathematics. — CRC Press, 1999. — ISBN 0-8493-9640-9.
  • Michael Hann. Structure and Form in Design: Critical Ideas for Creative Practice. — Bloomsbury Academic, 2012. — ISBN 9781847887429.
  • H. Cundy, A. Rollett. Mathematical Models. — 3rd. — Stradbroke, England : Tarquin Pub, 1952. 3.7 The Archimedean Polyhedra, pp. 101—115. P.118-119 Table I, Nets of Archimedean Duals, V.a.b.c… as vertically-regular symbols.
  • Peter Cromwell. Polyhedra. — Cambridge University Press, 1977. The Archimedean solids, p 156—167
  • Robert Williams. The Geometrical Foundation of Natural Structure. — Dover Publications, Inc., 1979. Uses Cundy-Rollett symbol
  • Branko Grünbaum; G. C. Shephard. Tilings and Patterns. — W. H. Freeman and Company, 1987. — ISBN 0-7167-1193-1. p58-64, Tilings of regular polygons a.b.c…. (мозаїка з правильних і зірчастих багатокутників) p. 95-97, 176, 283, 614—620, Monohedral tiling symbol [v1.v2. … .vr]. p632-642 hollow tilings
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5. (p289 Vertex figures, використовує кому як роздільник для архімедових тіл і мозаїк)

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.