Бруннове зачеплення

В теорії вузлів бруннове зачеплення — це нетривіальне зачеплення, яке розпадається при видаленні будь-якої з компонент. Іншими словами, розрізування будь-якого (топологічного) кільця розчіплює всі інші кільця (отже, жодні два з кілець не зчеплені, як у зачепленні Хопфа).

Це зачеплення з чотирьох компонент бруннове.
Бруннове зачеплення з шістьма компонентами.

Брунновими такі зачеплення названо на честь Германа Брунна, який у статті 1892 року Über Verkettung навів їх приклади.

Приклади
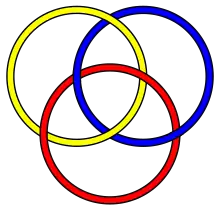
Кільця Борромео є найпростішим брунновим зачепленням.

Найвідомішим і найпростішим брунновим зачепленням є кільця Борромео — зачеплення трьох кілець. Однак для будь-якого числа, починаючи з трьох, існує нескінченне число бруннових зачеплень, що містить таке число кілець. Існує декілька відносно простих зачеплень з трьох компонент, які не еквівалентні кільцям Борромео:

  • Зачеплення з 12 перетинами.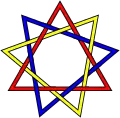
  • Зачеплення з 18 перетинами.
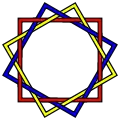  • Зачеплення з 24 перетинами.

Найпростіше бруннове зачеплення, відмінне від кілець Борромео (які мають 6 перетинів), напевно, зачеплення L10a140 з 10 перетинами[1].

Приклад n-компонентного бруннового зачеплення — це бруннове зачеплення «гумових кілець»[2], де кожна компонента охоплює попередню за схемою aba−1b−1 і останнє кільце зачіпляється за перше, утворюючи цикл.

Класифікація

Бруннові зачеплення описав з точністю до гомотопії Джон Мілнор у статті 1954 року[3], і інваріанти, запроваджені ним, тепер називаються інваріантами Мілнора

(n + 1)-компонентне зачеплення можна розуміти як елемент групи зачеплення n незачеплених компонент (група зачеплення в цьому випадку є фундаментальною групою доповнення зачеплення). Група зачеплення n незачеплених компонент є вільним добутком n твірних, тобто вільною групою Fn.

Не будь-який елемент групи Fn породжує бруннове зачеплення. Мілнор показав, що група елементів, відповідних брунновим зачепленням, пов'язана з градуйованою алгеброю Лі нижнього центрального ряду вільної групи, і її можна розуміти як «співвідношення» у вільній алгебрі Лі.

Добутки Массі

Бруннові зачеплення можна розуміти зо допомогою добутків Массі: добуток Массі — це n-членний добуток, який визначений тільки якщо всі (n − 1)-членні добутки перетворюються на нуль. Це відповідає властивості бруннового зачеплення, в якому всі набори з (n − 1) компонент не зчеплені, але всі n компонент разом утворюють нетривіальне зачеплення.

Бруннові коси
Звичайна коса є брунновою — після видалення чорної нитки синя опиняється над червоною так, що вони виявляються розчепленими. Те саме відбувається після видалення інших ниток.

Бруннова коса — це коса, яка стає тривіальною після видалення будь-якої з її ниток. Бруннові коси утворюють підгрупу в групі кіс. Бруннові коси на сфері, які не є брунновими на (плоскому) крузі, дають нетривіальні елементи в групах гомотопій сфери. Наприклад, «стандартна» коса, відповідна кільцям Борромео, дає розшарування Хопфа S3 → S2, і продовження такого плетива також дає бруннову косу.

Приклади з реального світу

Багато головоломок на розплутування та деякі механічні головоломки є варіантами бруннових зачеплень, і їх метою є звільнення якогось елемента, частково пов'язаного з іншою частиною головоломки.

Бруннові ланцюжки використовуються для створення декоративних прикрас з гумових кілець за допомогою пристроїв типу Wonder Loom або Rainbow Loom.

Примітки
  1. Dror Bar-Natan (2010-08-16). «All Brunnians, Maybe», [Academic Pensieve].
  2. "Rubberband" Brunnian Links. The Knot Atlas (англ.). Процитовано 5 серпня 2020.
  3. Milnor, 1954.

Література
  • A. J. Berrick, Frederick R. Cohen, Yan Loi Wong, Jie Wu. Configurations, braids, and homotopy groups // Journal of the American Mathematical Society. — 2006. — Т. 19, вип. 2. — С. 265–326. — DOI:10.1090/S0894-0347-05-00507-2..
  • Hermann Brunn, «Über Verkettung», J. Münch. Ber, XXII. 77-99 (1892). JFM 24.0507.01 (нім.)
  • John Milnor. Link Groups // Annals of Mathematics. — Annals of Mathematics, 1954. — Т. 59, вип. 2 (March). — С. 177–195. — DOI:10.2307/1969685. — JSTOR 1969685.
  • Dale Rolfsen (1976). Knots and Links. Berkeley: Publish or Perish, Inc. ISBN 0-914098-16-0.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.