Граф Дюрера
Граф Дюрера — неорієнтований кубічний граф з 12 вершинами і 18 ребрами. Граф названо ім'ям Альбрехта Дюрера, чия гравюра «Меланхолія» (1514) містила зображення так званого багатогранника Дюрера — опуклого багатогранника, кістяком якого є граф Дюрера. Багатогранник Дюрера є одним з чотирьох можливих добре покритих простих опуклих багатогранників.
Багатогранник Дюрера
Багатогранник Дюрера комбінаторно еквівалентний кубу з двома зрізаними протилежними вершинами, хоча на малюнку Дюрера він, швидше, зображений як зрізаний ромбоедр або тригранний зрізаний трапецоїд[1]. Точні геометричні властивості намальованого Дюрером багатогранника є предметом академічних суперечок, у яких припускаються різні гіпотетичні значення (гострих) кутів від 72° до 82°[2].
Властивості графу
Граф Дюрера — це граф, утворений вершинами і ребрами багатогранника Дюрера. Граф є кубічним з обхватом 3 і діаметром 4. Оскільки граф є кістяком багатогранника Дюрера, його можна отримати, застосувавши перетворення трикутник-зірка протилежних вершин графу куба, або як узагальнений граф Петерсена . Як і будь-який інший граф опуклого багатогранника, граф Дюрера є вершинно 3-зв'язним простим планарним графом.
Граф Дюрера є добре покритим, що означає, що всі його найбільші незалежні множини мають однакове число вершин — чотири. Граф є одним з добре покритих кубічних багатогранних графів і одним з семи добре покритих 3-зв'язних кубічних графів. Іншими трьома добре покритими простими опуклими багатогранниками є тетраедр, трикутна призма і п'ятикутна призма[3][4].
Граф Дюрера є гамільтоновим з LCF-позначенням [-4,5,2,-4,-2,5;-][5]. Точніше, граф має рівно шість гамільтонових циклів, кожну пару яких можна відобразити в будь-яку іншу симетріями графу[6].
Симетрії
Група автоморфізмів як графу Дюрера, так і багатогранника Дюрера (у вигляді зрізаного куба або у формі, наведеній Дюрером) ізоморфна діедральній групі порядку 12.
Галерея
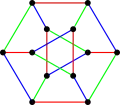 Хроматичний індекс графу Дюрера дорівнює 3.
Хроматичний індекс графу Дюрера дорівнює 3. Хроматичне число графу Дюрера дорівнює 3.
Хроматичне число графу Дюрера дорівнює 3. Граф Дюрера гамільтонів.
Граф Дюрера гамільтонів.
Примітки
- Вебер, 1900.
- Вайцель, 2004.
- Кэмпбелл, Пламмер, 1988.
- Кэмпбелл, Эллингхэм, Ройл, 1993.
- Кастанья і Прінс (Кастанья, Прінс, (1972)) приписують доведення гамільтоновості класу узагальнених графів Петерсена, до якого належить граф Дюрера, тезам дисертації 1968 року Робертсона (G. N. Robertson) з університету Ватерлоо.
- Швенк, (1989).
Література
- S. R. Campbell, M. N. Ellingham, Gordon F. Royle. A characterisation of well-covered cubic graphs // Journal of Combinatorial Mathematics and Combinatorial Computing. — 1993. — Т. 13 (17 лютого). — С. 193–212.
- Stephen R. Campbell, Michael D. Plummer. On well-covered 3-polytopes // Ars Combinatoria. — 1988. — Т. 25, вип. A (17 лютого). — С. 215–242.
- Frank Castagna, Geert Prins. Every Generalized Petersen Graph has a Tait Coloring // Pacific Journal of Mathematics. — 1972. — Т. 40 (17 лютого). — DOI:.
- Allen J. Schwenk. Enumeration of Hamiltonian cycles in certain generalized Petersen graphs // Journal of Combinatorial Theory. — 1989. — Т. 47, вип. 1 (17 лютого). — С. 53–59. — (Series B). — DOI:.
- P. Weber. Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus. — Strassburg, 1900. — 17 лютого. (як процитовано у Вайцеля (Вайцель, (2004)).
- Hans Weitzel. A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I // Historia Mathematica. — 2004. — Т. 31, вип. 1 (17 лютого). — С. 11–14. — DOI:.
