Граф Пелі
В теорії графів графами Пелі (на честь Раймонда Пелі) називають щільні неорієнтовані графи, побудовані з членів відповідного скінченного поля шляхом з'єднання пар елементів, що відрізняються на квадратичний лишок. Графи Пелі утворюють нескінченне сімейство конференсних графів, оскільки тісно пов'язані з нескінченним сімейством симетричних конференс-матриць. Графи Пелі дають можливість застосувати теоретичні засоби теорії графів у теорії квадратичних лишків і мають цікаві властивості, що робить їх корисними для теорії графів загалом.
| Граф Пелі | |
|---|---|
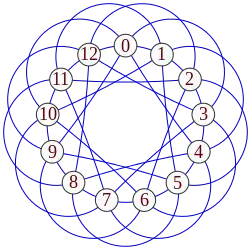 Граф Пелі порядку 13 | |
| Названий на честь | Раймонд Пелі |
| Вершин |
q ≡ 1 mod 4, q — степінь простого числа |
| Ребер | q(q − 1)/4 |
| Діаметр | 2 |
| Властивості |
сильно регулярний конференсний самодоповняльний |
| Позначення | QR(q) |
Графи Пелі тісно пов'язані з побудовою Пелі для побудови матриць Адамара з квадратичних лишків (Пелі, 1933)[1]. Як графи їх незалежно ввели Закс (Sachs, 1962) і Ердеш спільно з Реньї (Erdős, Rényi, 1963)[2]. Горст Закс (Horst Sachs) цікавився ними через їхню властивість самодоповнюваності, тоді як Ердеш і Реньї вивчали їхні симетрії.
Орграфи Пелі є прямим аналогом графів Пелі і відповідають антисиметричним конференс-матрицям. Їх увели Грем і Спенсер[3] (і, незалежно, Закс, Ердеш і Реньї) як шлях побудови турніру з властивостями, раніше відомими тільки для випадкових турнірів: в орграфах Пелі підмножина вершин домінується будь-якою вершиною.
Визначення
Нехай q — степінь простого числа, такий, що q = 1 (mod 4). Зауважимо, що звідси випливає існування квадратного кореня з −1 в єдиному скінченному полі Fq, що має порядок q.
Нехай також V = Fq і
- .
Ця множина коректно визначена, оскільки a − b = −(b − a), і −1 є квадратом якогось числа, звідки випливає, що a − b є квадратом тоді і лише тоді, коли b − a є квадратом.
За визначенням G = (V, E) — граф Пелі порядку q.
Приклад
Задля q = 13 поле Fq утворюється числами за модулем 13. Числа, що мають квадратні корені за модулем 13:
- ±1 (квадратні корені ±1 для +1, ±5 для −1)
- ±3 (квадратні корені ±4 для +3, ±6 для −3)
- ±4 (квадратні корені ±2 для +4, ±3 для −4).
Таким чином, граф Пелі утворюють вершини, які відповідають числам з інтервалу [0,12], і кожна вершина x з'єднана з шістьма сусідами: x ± 1 (mod 13), x ± 3 (mod 13), і x ± 4 (mod 13).
Властивості
- Графи Пелі є самодоповняльним — доповнення будь-якого графа Пелі ізоморфне самому графу[4].
- Ці графи сильно регулярні з параметрами
- До того ж графи Пелі, фактично, утворюють нескінченне сімейство конференсних графів.
- Власні значення графів Пелі — це числа (з кратністю 1) і (обидва з кратністю ) і можуть бути обчислені за допомогою квадратичних сум Гауса.
- Якщо q — просте, межами ізопериметричного числа i(G) будуть:
- Звідси випливає, що i(G)~O (q), і граф Пелі є експандер.
- Якщо q — просте, його граф Пелі є гамільтоновим циклом циркулянтного графа.
- Графи Пелі квазівипадкові (Чанг та ін., 1989)[5] — число випадків, коли граф сталого порядку виявиться підграфом графа Пелі, дорівнює (в границі для великих q) тим самим, що й для випадкових графів, а за великих множин вершин має приблизно таке саме число ребер, що й у випадкових графів.
Застосування
- Граф Пелі 17-го порядку є єдиним найбільшим графом G, таким, що ні він сам, ні його доповнення не містять повного підграфа з 4 вершинами (Еванс та ін., 1981).[6] З цього випливає, що число Рамсея R(4, 4) = 18.
- Граф Пелі 101-го порядку поки єдиний відомий максимальний граф G, такий, що ні G, ні його доповнення не містять повного підграфа з 6 вершинами.
- Сасакура[7] використовував графи Пелі для узагальнення побудови пучка Горрокса — Мамфорда.
Орграфи Пелі
Нехай q — степінь простого числа, такий, що q = 3 (mod 4). Тоді скінченне поле Fq порядку q не має квадратного кореня з −1. Отже, для будь-якої пари (a,b) різних елементів Fq або a − b, або b − a, але не обидва, є квадратами. Орграф Пелі — це орієнтований граф зі множиною вершин V = Fq і множиною дуг
Орграф Пелі є турніром, оскільки кожна пара різних вершин пов'язана дугою в одному і тільки в одному напрямку.
Орграф Пелі веде до побудови деяких антисиметричних конференс-матриць і двоплощинної геометрії.
Рід графа
Шість сусідів кожної вершини в графі Пелі 13-го порядку з'єднані в цикл, так що граф локально циклічний. Таким чином, цей граф можна вкласти в тріангуляцію Вітні тора, в якій кожна грань є трикутником і кожен трикутник є гранню. У загальнішому випадку, якщо який-небудь граф Пелі порядку q можна вкласти таким чином, що всі його грані є трикутниками, ми можемо обчислити рід результуючої поверхні за допомогою ейлерової характеристики . Могар (Bojan Mohar, 2005) висловив гіпотезу, що мінімальний рід поверхні, в яку можна вкласти граф Пелі, десь біля цього значення в разі, якщо q є квадратом, і поставив питання, чи можна узагальнити такі межі. Зокрема, Могар припустив, що графи Пелі квадратного порядку можна вкласти в поверхні роду
де член o(1) може бути будь-якою функцією від q, яка прямує до нуля при прямуванні q до нескінченності.
Вайт (White, 2001)[8] знайшов вкладення графів Пелі порядку q ≡ 1 (mod 8), узагальнюючи природне вкладення графа Пелі 9-го порядку як квадратної ґратки на тор. Однак рід вкладення Вітні вищий приблизно в три рази від межі, яку Могар назвав у своїй гіпотезі.
Посилання
- R. E. A. C. Paley. On orthogonal matrices // J. Math. Phys.. — Т. 12. — С. 311–320.
- Asymmetric graphs // Acta Mathematica Academiae Scientiarum Hungaricae. — 1963. — Т. 14, вип. 3–4 (7 лютого). — С. 295–315. — DOI:.
- R. L. Graham, J. H. Spencer. A constructive solution to a tournament problem // Canadian Mathematical Bulletin. — 1971. — Т. 14 (7 лютого). — С. 45–48. — DOI:.
- Horst Sachs. Über selbstkomplementäre Graphen // Publicationes Mathematicae Debrecen. — 1962. — Т. 9 (7 лютого). — С. 270–288.
- Chung, Fan R. K., Р. Грэм, R. M. Wilson,. Quasi-random graps // Combinatorica. — 1989. — Т. 9, вип. 4 (7 лютого). — С. 345–362. — DOI:.
- Evans, R. J.; Pulham, J. R.; Sheehan, J. On the number of complete subgraphs contained in certain graphs // Journal of Combinatorial Theory, Series B. — 1981. — Т. 30, вип. 3 (7 лютого). — С. 364–371. — DOI:.
- Sasakura, Nobuo; Enta, Yoichi; Kagesawa, Masataka. Construction of rank two reflexive sheaves with similar properties to the Horrocks–Mumford bundle // Proc. Japan Acad., Ser. A. — 1993. — Т. 69, вип. 5 (7 лютого). — С. 144–148. — DOI:.
- White, A. T. Graphs of groups on surfaces // Interactions and models. — Amsterdam : North-Holland Mathematics Studies 188, 2001.
Література
- Baker, R. D.; Ebert, G. L.; Hemmeter, J.; Woldar, A. J. Maximal cliques in the Paley graphs of square order // J. Statist. Plann. Inference. — 1996. — Т. 56 (7 лютого). — С. 33–38. — DOI:.
- Broere, I.; Döman, D.; Ridley, J. N. The clique numbers and chromatic numbers of certain Paley graphs // Quaestiones Mathematicae. — 1988. — Т. 11 (7 лютого). — С. 91–93. — DOI:.
Посилання
- Brouwer, Andries E. Paley graps.[недоступне посилання з Июнь 2018]
- Mohar, Bojan (2005). PaleyGenus.html Genus of Paley graps.[недоступне посилання з Сентябрь 2018]