Дерево пошуку Монте-Карло

У інформатиці дерево пошуку Монте-Карло (англ. Monte Carlo tree search, ДПМК) — це евристичний алгоритм пошуку який можна використати для деяких видів процесів ухвалення рішень, а особливо для тих, які використовуються в програмному забезпеченні, яке грає в настільні ігри з дошкою. У цьому контексті ДПМК використовується для побудови дерева гри.

У 2016 році ДПМК та нейронна мережа були об'єднанні для гри в Ґо.[1] Також цей алгоритм використовували в інших настільних іграх, таких як: шахи та сьоґі; іграх з неповною інформацією, таких як бридж[2] і покер[3], а також у покрокових стратегічних відеоіграх (наприклад, Total War: Rome II в компанії зі штучним інтелектом високої складності[4]). ДПМК також використовувався в автомобілях з автопілотом. Його, наприклад використали в програмному забезпеченні Tesla Autopilot.[5]

Історія

Метод Монте-Карло

Метод Монте-Карло бере свій початок з 1940-х років. Він використовує випадкову вибірку для детерміністичних задач, які важко або неможливо вирішити за допомогою інших підходів. У своїй докторській дисертації 1987 року Брюс Абрамсон об'єднав мінімаксний пошук із моделлю очікуваного результату, яка використовує випадковий вибір дії у гри до кінця, замість оцінювальної функції, яку використовують зазвичай. Абрамсон сказав, що модель очікуваного результату «виявилась точною, легко передбачувальною, такою, що можливо ефективно обчислити та можна легко використати незалежною від сфери завдання».[6] Він багато експериментував з хрестиками-ноликами, а потім з оцінювальними функціями, які було згенеровано машиною для реверсі та шахів.

Потім такий метод було досліджено та успішно застосовано В. Ертелом, Дж. Шуманом та К. Зутнером у 1989 році для евристичного пошуку в області автоматизованого доведення теорем[7][8][9], таким чином зменшуючи час виконання з експоненціального неінформованих алгоритмів пошуку, таких як, пошук у ширину, пошук у глибину або з пошук в глибину з ітеративним заглибленням.

У 1992 році Б. Брюгманн вперше застосував його для гри в Ґо.[10] У 2002 році Чанг та інші[11] запропонували ідею «рекурсивного розгортання та зворотного відстеження» з «адаптивним» вибором вибірки у своєму алгоритмі адаптивної багатоступеневої вибірки (англ. Adaptive Multi-stage Sampling, AMS) для моделі процесів прийняття рішень Маркова. АБВ був першим алгоритмом, який використав ідею розвідки та експлуатації на основі UCB для побудови дерев вибірки/моделювання (Монте-Карло) і послужив основою для верхніх дерев довіри (англ. Upper Confidence Trees, UCT).[12]

Дерево пошуку Монте-Карло

Рейтинг найкращих програм для гри в Ґо на сервері KGS з 2007 року. З 2006 року всі найкращі програми використовують алгоритм дерева пошуку Монте-Карло.[13]

У 2006 році, натхненний попередниками,[14] Ремі Колум описав застосування методу Монте-Карло для побудови дерева ігор і придумав назву: «Дерево Пошуку Монте-Карло»[15] Л.Коксіс та Кс. Шепешварі розробили алгоритм UCT (Верхніх меж довіри, які застосовуються до дерев)[16] а С. Геллі та інші впровадили UCT у свою програму MoGo.[17] У 2008 році MoGo досягла рівня дан (майстер) у Го 9×9,[18] і програма Fuego почала перемагати у сильних гравців-аматорів у Го 9×9.[19]

У січні 2012 року програма Дзен перемогла з рахунком 3:1 у матчі Го на дошці 19×19 з гравцем-аматором з 2 даном.[20] Google Deepmind розробив програму AlphaGo, яка в жовтні 2015 року стала першою програмою гри в Ґо, яка змогла обіграти професійного гравця в Ґо без фори на повнорозмірній дошці 19x19.[1][21][22] У березні 2016 року AlphaGo отримав почесний рівень 9 дану (майстер) у Ґо 19×19 за перемогу над Лі Седолом у серії з п'ятьох ігор з підсумковим рахунком чотири перемоги проти однієї поразки.[23] AlphaGo являє собою значне покращення в порівнянні з попередніми програмами гри в Ґо. Також вона знаменувала нову віху в машинному навчанні, оскільки вона використовує дерево пошуку Монте-Карло у поєднанні зі штучною нейронною мережею (метод глибинного навчання) для розробки стратегії, який є ефективним і значно перевершує попередні програми.[24]

Алгоритм ДПМК також використовували в програмах, які грали в інші настільні ігри на спеціальній дошці (Гекс,[25] Гаванна,[26] Ігри Амазонок,[27] і Арімаа[28]), відеоігри в реальному часі (наприклад, Ms. Pac-Man[29][30] і Fable Legends[31]), а також недетерміновані ігри (такі як скат,[32] покер,[3] Magic: The Gathering,[33] або Колонізатори[34]).

Принцип дії

Основна ідея ДПМК полягає в аналізі найбільш перспективних ходів, розширені дерева пошуку на основі випадкової вибірки даних простору пошуку. Застосування дерева пошуку Монте-Карло в іграх базується на багатьох відтвореннях, які також називаються розгортаннями. У кожному відтворені гри розгортається до самого кінця шляхом вибору ходу випадковим чином. Кінцевий результат гри кожного розігруванні потім використовується для побудови ваги вузлів у дереві гри, щоб обирати вузли, які призведуть до кращих результатів у майбутніх розігруваннях.

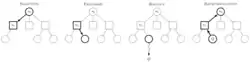
Найпростіший спосіб використання розігрувань — це застосовувати однакову кількість розігрувань після кожного дозволеного ходу поточного гравця, а потім обрати хід, який привів до найбільшої кількості перемог.[10] Ефективність цього методу, який називається чистий ігровий пошук Монте-Карло, часто зростає з часом, оскільки було проведено більше розіграшів для ходів, які частіше призводили до перемоги поточного гравця у порівнянні з попередніми розігруваннями. Кожен раунд побудови дерева пошуку Монте-Карло складається з чотирьох кроків:[35]

Вибір: Починаючи з кореня дерева $R$ обійти послідовно дочірні вузли, поки не буде досягнуто вузол $L$ . $R$ — це поточний стан гри, а лист — це будь-який вузол, у якого потенційно існує дочірній елемент, з якого ще не було ініційовано симуляцію (відтворення). Розділ нижче розповідає більше про спосіб зміщення вибору дочірніх вузлів, що дозволяє дереву гри розширюватися саме до найперспективніших ходів, що і є сутністю дерева пошуку Монте-Карло.
Розширення: Якщо $L$ закінчує гру (наприклад, перемога/програш/нічия) для будь-якого гравця, створіть один (або більше) дочірніх вузлів і виберіть вузол $C$ поміж них. Дочірні вузли — це будь-які ходи в межах правил з ігрової позиції $L$ .
Симуляція: завершите одне випадкове розігрування з вузла $C$ . Цей крок іноді також називають відтворенням або розгортанням. Для вибору розігрування можна використати простий алгоритм, як, наприклад вибір рівномірно випадкових ходів до того моменту, як партія буде закінчена (наприклад, у шахах партія виграна, програна чи нічия).
Зворотне поширення: використовуйте результат симуляції для оновлення інформації у вузлах між $C$ та $R$

Крок у алгоритмі дерева пошуку Монте-Карло.

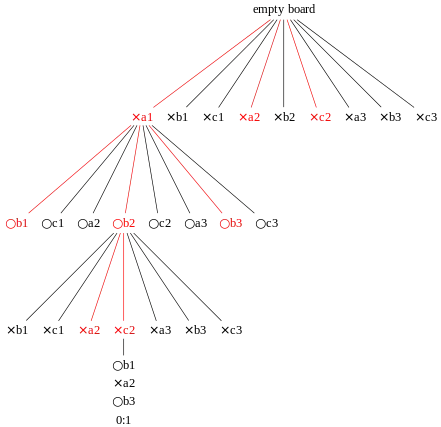
Цей графік показує частину алгоритму вибору одного рішення, де кожен вузол показує відношення виграшів до загальної кількості розіграшів з цієї точки в дереві гри для гравця, який представляє цей вузол.[36] На діаграмі той, який грає за чорних, має прийняти рішення. Судячи з кореневого вузла, білі з цієї позиції виграли 11 з 21 ігор. Також виходить, що чорні перемогли в 10 з 21 ігор, що виходить, якщо скласти значення трьох чорних вузлів під ним, які представляють можливі ходи чорних.

Якщо білі програють симуляцію, всі вузли на шляху вибору збільшують свою кількість симуляції (знаменник), і тільки чорні вузли збільшують кількість перемог перемогою (чисельник). Якщо переможуть білі, усі вузли на шляху все одно збільшать кількість симуляцій, і тільки білим зарахується перемога. У іграх, де можлива нічия, вона призводить до збільшення чисельника для обох на 0,5, а знаменника на 1. Це гарантує, що під час розрахунку вибір кожного гравця розширюється до найперспективніших ходів, для того, щоб максимізувати цінність свого ходу.

Поки є час, відведений на хід, процес пошуку повторюється. Потім, в якості остаточної відповіді, вибирається хід з найбільшою кількістю зроблених симуляцій (тобто найбільшим знаменником).

Чистий ігровий пошук Монте-Карло

Цю базову процедуру можна застосувати до будь-якої гри з кінцевою кількістю ходів кінцевої довжини. Для кожної позиції визначаються всі можливі ходи: k випадкових ігор розігруються до самого кінця, а результати зберігаються. Обирається хід, який веде до найкращого результату. Зв'язки розриваються за допомогою підкидання монети. Чистий ігровий пошук Монте-Карло дає гарні результати при декількох іграх з випадковими елементами, як, наприклад у грі EinStein würfelt nicht!. Він сходиться до оптимальної стратегії (якщо k наближається до нескінченності) у настільних іграх із випадковим порядком ходу, наприклад у Гекс.[37] AlphaZero від DeepMind замінив етап симуляції на використання оцінки на основі нейронної мережі.[2]

Розвідка та експлуатація

Основна складність у виборі дочірніх вузлів полягає в підтримці певного балансу між експлуатацією глибоких варіантів після ходів з високим середнім виграшем і розвідкою ходів з невеликою кількістю симуляцій. Першу формулу для балансування експлуатації та розвідки в іграх, яка називається UCT (Upper Confidence Bound 1, яку було застосовано до дерев), було виведено Левенте Кочисом і Чаба Шепешварі.[16] UCT базується на формулі UCB1, виведеної Ауером, Чеза-Біанкі та Фішером[38], і на доказі збіжності алгоритму АБВ (англ. Adaptive Multi-stage Sampling), який було вперше застосовано до багатоступеневих моделей прийняття рішень (зокрема, Марковський процес прийняття рішень) Чангом, Фу, Ху і Маркусом.[11] Кочис і Шепешварі рекомендували обирати в кожному вузлі дерева гри хід, для якого вираз ${\frac {w_{i}}{n_{i}}}+c{\sqrt {\frac {\ln N_{i}}{n_{i}}}}$ набуває найбільшого значення. У цій формулі:

$w i$ означає кількість виграшів для вузла після i-го ходу
$n i$ означає кількість симуляцій для вузла після i-го переміщення
$N i$ означає загальну кількість симуляцій батьківського вузла після i-го переміщення
$c$ параметр розвідки, теоретично рівний $\sqrt 2$ ; на практиці зазвичай вибирається емпірично

Ліва частина формули вище відповідає за експлуатацію; вона має велике значення для ходів з високим середнім коефіцієнтом виграшу. Права частина відповідає за розвідку; вона висока для ходів з невеликою кількістю симуляцій.

Більшість сучасних реалізацій дерева пошуку Монте-Карло базуються на варіанті UCT, який базується на АБВ: алгоритмі оптимізації моделювання для оцінки функції значення в кінцевих горизонтах Марковських процесів(MDP), представлених Чангом та ін.[11] (2005) у дослідженні операцій. (АБВ була першою роботою, яка досліджувала ідею розвідки та експлуатації на основі UCB при побудові вибіркових/модельованих дерев (Монте-Карло) і була основою для UCT.[12])

Переваги та недоліки

Хоча було доведено, що оцінка ходів у дереві пошуку Монте-Карло сходиться до мінімакса[39], базова версія дерева пошуку Монте-Карло збігається лише в так званих іграх «Monte Carlo Perfect».[40] Однак дерево пошуку Монте-Карло має значні переваги у порівняні з альфа-бета відсіченням та подібними алгоритмами, що мінімізують простір пошуку.

Зокрема, чистий пошук дерева Монте-Карло не потребує явної оцінювальної функції. Для дослідження простору пошуку (тобто генерування дозволених ходів з заданої позиції та умов закінчення гри) достатньо реалізації механіки гри. Дерево пошуку Монте-Карло можна використовувати в іграх без розробленої теорії або в універсальних ігрових програмах.

Дерево гри в алгоритмі дерева пошуку Монте-Карло зростає асиметрично, оскільки метод концентрується на найперспективніших піддеревах. Таким чином він досягає кращих результатів, у порівняні з класичними алгоритмами в іграх з високим коефіцієнтом розгалуження.

Недоліком алгоритму є те, що в певних позиціях можуть бути ходи, які виглядають, на перший погляд, перспективними, але насправді призводять до програшу. Такі «стани пастки» вимагають ретельного аналізу та правильної обробки, особливо під час гри проти досвідченого гравця; однак ДПМК може не «помічати» такі лінії через свою стратегію вибіркового розширення вузлів.[41][42] Вважається, що це могло бути однією з причин поразки AlphaGo у четвертій грі проти Лі Седола через те, що алгоритм намагається обрізати менш релевантні послідовності. У деяких випадках гра може призвести до дуже специфічної лінії гри, яка є важливою, проте яку не помічає алгоритм і обрізає його. Така лінія знаходиться «поза радаром пошуку».[43]

Покращення

Для скорочення часу пошуку були запропоновані різні модифікації основного методу алгоритму дерева пошуку Монте-Карло. Деякі покращення виходять зі знання певної області, інші ні.

Дерево пошуку Монте-Карло може використовувати як легкі, так і важкі розігрування. Легкі розігрування складаються з випадкових ходів, тоді як важкі розігрування застосовують різні евристичні методи, щоб впливати на вибір ходів.[44] Ці евристичні методи можуть використовувати результати попередніх розіграшів (наприклад, метод останньої гарної відповіді[45]) або експертні знання даної гри. Наприклад, у багатьох програмах для гри в Ґо певні візерунки каменів на частині дошки впливають на ймовірність переміщення в цю область.[17] Парадоксально, але неоптимальна гра в симуляції іноді робить програму дерева пошуку Монте-Карло сильніше в кінцевому розрахунку.[46]

Візерунки хане (оточення каменів супротивника), які використовуються в розігруваннях програмою MoGo. Для чорного і білого вигідно поставити камінь на середній квадрат, за винятком крайнього правого візерунка, де він віддає перевагу лише чорному.[17]

При побудові дерева гри можуть бути використані знання, що стосуються предметної області для того, щоб експлуатувати деякі варіанти. Один з таких методів призначає ненульові значення виграним і зіграним симуляціям під час створення кожного дочірнього вузла. Це призводить до штучно підвищення або зниження середнього рівня виграшу, що призводить до того, що вузол вибирається частіше або рідше.[47] Схожий метод, який називається прогресивним зміщенням, полягає в додаванні до формули UCB1 ${\frac {b_{i}}{n_{i}}}$ , де $b i$ — евристична оцінка $i$ -го ходу.[35]

Базовий алгоритм дерева пошуку Монте-Карло збирає достатньо інформації для того, щоб знайти найбільш перспективні ходи, лише після багатьох раундів; до тих пір його рішення майже випадкові. Ця фаза розвідки може бути значно зменшена в певному класі ігор із використанням RAVE (Rapid Action Value Estimation).[47] У цих іграх перестановки послідовності ходів призводять до того ж положення. Як правило, це настільні ігри, в яких хід передбачає розміщення фігури або каменя на дошці. У таких іграх на цінність кожного ходу часто майже не впливають інші ходи.

У RAVE для даного вузла дерева ігор $N$ його дочірні вузли $C i$ зберігають не тільки статистику перемог у розігруваннях, розпочатих у вузлі $N$ , але і статистику перемог у всіх розіграшах, які було розпочато у вузлі $N$ і нижче, якщо вони містять це переміщення. Таким чином, на вміст вузлів дерева впливають не тільки ходи, які виконуються в даній позиції, але й ті ходи, які виконуються пізніше.

RAVE на прикладі хрестиків-нуликів. У червоних вузлах статистика RAVE буде оновлена після моделювання b1-a2-b3.

При використанні RAVE під час етапу вибору обирається вузол, для якого модифікована формула UCB1 $(1-\beta (n_{i},{\tilde {n}}_{i})){\frac {w_{i}}{n_{i}}}+\beta (n_{i},{\tilde {n}}_{i}){\frac {{\tilde {w}}_{i}}{{\tilde {n}}_{i}}}+c{\sqrt {\frac {\ln t}{n_{i}}}}$ має найбільше значення. У цій формулі:

${\tilde {w}}_{i}$ — це кількість виграних розігрувань, які містять хід $i$ .
${\tilde {n}}_{i}$ - це кількість усіх розігрувань, які містять хід $i$ .
$\beta (n_{i},{\tilde {n}}_{i})$ — функція, яка наближається до одиниці для відносно малих $n i$ і до нуля для відносно великих ${\tilde {n}}_{i}$ .

Одна з багатьох формул для $\beta (n_{i},{\tilde {n}}_{i})$ , яку запропонував Д. Сільвер,[48] стверджує, що в збалансованих позиціях можна вважати, що $\beta (n_{i},{\tilde {n}}_{i})={\frac {{\tilde {n}}_{i}}{n_{i}+{\tilde {n}}_{i}+4b^{2}n_{i}{\tilde {n}}_{i}}}$ , де $b$ — емпірично обрана константа.

Обрахунки, що використовується в алгоритмі дерева пошуку Монте-Карло, часто залежать від багатьох параметрів. Існують автоматизовані методи налаштування параметрів, щоб максимізувати виграш.[49]

Дерево пошуку Монте-Карло може одночасно обраховуватись багатьма потоками або процесами. Існує декілька принципово різних методів його паралельного виконання:[50]

Паралелізація листів, тобто паралельне виконання багатьох розігрувань одного листа ігрового дерева.
Коренева паралелізація, тобто паралельне створення незалежних ігрових дерев, які виконують ходи на основі коренів всіх цих дерев.
Паралелізація дерева, тобто паралельна побудова одного ігрового дерева, яке захищає дані від одночасного запису за допомогою одного глобального мьютексу, з кількома м'ютексами або з неблокуючою синхронізацією.[51]

Див. також

AlphaGo, програма для Ґо, що використовує дерево пошуку Монте-Карло, навчання з підкріпленням і глибоке навчання.
AlphaGo Zero, оновлена програма для Ґо, що використовує дерево пошуку Монте-Карло, навчання з підкріпленням і глибоке навчання.
AlphaZero, узагальнена версія AlphaGo Zero з використанням дерева пошуку Монте-Карло, навчання з підкріпленням і глибокого навчання.
Leela Chess Zero, безкоштовна програмна реалізація методів AlphaZero для гри в шахи, які на даний момент є однією з провідних програм для гри в шахи.

Примітки

Silver, David; Huang, Aja; Maddison, Chris J.; Guez, Arthur; Sifre, Laurent; Driessche, George van den; Schrittwieser, Julian; Antonoglou, Ioannis та ін. (28 січня 2016). Mastering the game of Go with deep neural networks and tree search. Nature 529 (7587): 484–489. Bibcode:2016Natur.529..484S. ISSN 0028-0836. PMID 26819042. doi:10.1038/nature16961.
>Artificial Intelligence: A Modern Approach (вид. 3rd). Prentice Hall. 2009.
Jonathan Rubin; Ian Watson (April 2011). Computer poker: A review. Artificial Intelligence 175 (5–6): 958–987. doi:10.1016/j.artint.2010.12.005. Архів оригіналу за 13 серпня 2012.
Monte-Carlo Tree Search in TOTAL WAR: ROME II's Campaign AI. AI Game Dev. Архів оригіналу за 13 березня 2017. Процитовано 25 лютого 2017.
Tesla's AI Day video https://youtube.com/watch?v=j0z4FweCy4M
Abramson, Bruce (1987). The Expected-Outcome Model of Two-Player Games. Technical report, Department of Computer Science, Columbia University. Процитовано 23 грудня 2013.
Wolfgang Ertel; Johann Schumann; Christian Suttner (1989). Learning Heuristics for a Theorem Prover using Back Propagation.. У J. Retti. 5. Österreichische Artificial-Intelligence-Tagung. Informatik-Fachberichte 208,pp. 87-95. Springer.
Christian Suttner; Wolfgang Ertel (1990). Automatic Acquisition of Search Guiding Heuristics.. CADE90, 10th Int. Conf. on Automated Deduction.pp. 470-484. LNAI 449. Springer.
Christian Suttner; Wolfgang Ertel (1991). Using Back-Propagation Networks for Guiding the Search of a Theorem Prover.. Journal of Neural Networks Research & Applications 2 (1): 3–16.
Brügmann, Bernd (1993). Monte Carlo Go. Technical report, Department of Physics, Syracuse University.
Chang, Hyeong Soo; Fu, Michael C.; Hu, Jiaqiao; Marcus, Steven I. (2005). An Adaptive Sampling Algorithm for Solving Markov Decision Processes. Operations Research 53: 126–139. doi:10.1287/opre.1040.0145.
Hyeong Soo Chang; Michael Fu; Jiaqiao Hu; Steven I. Marcus (2016). Google DeepMind's Alphago: O.R.'s unheralded role in the path-breaking achievement. OR/MS Today 45 (5): 24–29.
Sensei's Library: KGSBotRatings. Процитовано 3 травня 2012.
Rémi Coulom (2008). The Monte-Carlo Revolution in Go. Japanese-French Frontiers of Science Symposium.
Rémi Coulom (2007). Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. Computers and Games, 5th International Conference, CG 2006, Turin, Italy, May 29–31, 2006. Revised Papers. Springer. с. 72–83. ISBN 978-3-540-75537-1.
. ISBN 3-540-45375-X. Пропущений або порожній |title= (довідка)
Sylvain Gelly; Yizao Wang; Rémi Munos; Olivier Teytaud (November 2006). Modification of UCT with Patterns in Monte-Carlo Go. Technical report, INRIA.
Chang-Shing Lee; Mei-Hui Wang; Guillaume Chaslot; Jean-Baptiste Hoock; Arpad Rimmel; Olivier Teytaud; Shang-Rong Tsai; Shun-Chin Hsu та ін. (2009). The Computational Intelligence of MoGo Revealed in Taiwan's Computer Go Tournaments. IEEE Transactions on Computational Intelligence and AI in Games 1 (1): 73–89. doi:10.1109/tciaig.2009.2018703.
Markus Enzenberger; Martin Mūller (2008). Fuego – An Open-Source Framework for Board Games and Go Engine Based on Monte Carlo Tree Search. Technical report, University of Alberta.
The Shodan Go Bet. Процитовано 2 травня 2012.
Research Blog: AlphaGo: Mastering the ancient game of Go with Machine Learning. Google Research Blog. 27 січня 2016.
Google achieves AI 'breakthrough' by beating Go champion. BBC News. 27 січня 2016.
Match 1 - Google DeepMind Challenge Match: Lee Sedol vs AlphaGo. Youtube. 9 березня 2016.
Google AlphaGo AI clean sweeps European Go champion. ZDNet. 28 січня 2016.
Broderick Arneson; Ryan Hayward; Philip Henderson (June 2009). MoHex Wins Hex Tournament. ICGA Journal 32 (2): 114–116. doi:10.3233/ICG-2009-32218.
Timo Ewalds (2011). Playing and Solving Havannah. Master's thesis, University of Alberta.
Richard J. Lorentz (2008). Amazons Discover Monte-Carlo. Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. Springer. с. 13–24. ISBN 978-3-540-87607-6.
Tomáš Kozelek (2009). Methods of MCTS and the game Arimaa. Master's thesis, Charles University in Prague.
Xiaocong Gan; Yun Bao; Zhangang Han (December 2011). Real-Time Search Method in Nondeterministic Game – Ms. Pac-Man. ICGA Journal 34 (4): 209–222. doi:10.3233/ICG-2011-34404.
Tom Pepels; Mark H. M. Winands; Marc Lanctot (September 2014). Real-Time Monte Carlo Tree Search in Ms Pac-Man. IEEE Transactions on Computational Intelligence and AI in Games 6 (3): 245–257. doi:10.1109/tciaig.2013.2291577.
Mountain, Gwaredd (2015). Tactical Planning and Real-time MCTS in Fable Legends. Процитовано 8 червня 2019. «.. we implemented a simulation based approach, which involved modelling the game play and using MCTS to search the potential plan space. Overall this worked well, ...»
Michael Buro; Jeffrey Richard Long; Timothy Furtak; Nathan R. Sturtevant (2009). Improving State Evaluation, Inference, and Search in Trick-Based Card Games. IJCAI 2009, Proceedings of the 21st International Joint Conference on Artificial Intelligence, Pasadena, California, USA, July 11–17, 2009. с. 1407–1413.
C.D. Ward; P.I. Cowling (2009). Monte Carlo Search Applied to Card Selection in Magic: The Gathering. CIG'09 Proceedings of the 5th international conference on Computational Intelligence and Games. IEEE Press. Архів оригіналу|archiveurl= вимагає |url= (довідка) за 28 травня 2016.
István Szita; Guillaume Chaslot; Pieter Spronck (2010). Monte-Carlo Tree Search in Settlers of Catan. У Jaap Van Den Herik. Advances in Computer Games, 12th International Conference, ACG 2009, Pamplona, Spain, May 11–13, 2009. Revised Papers. Springer. с. 21–32. ISBN 978-3-642-12992-6.
G.M.J.B. Chaslot; M.H.M. Winands; J.W.H.M. Uiterwijk; H.J. van den Herik; B. Bouzy (2008). Progressive Strategies for Monte-Carlo Tree Search. New Mathematics and Natural Computation 4 (3): 343–359. doi:10.1142/s1793005708001094.
Bradberry, Jeff (7 вересня 2015). Introduction to Monte Carlo Tree Search.
Peres, Yuval (2006). «Random-Turn Hex and other selection games». arXiv:abs/math/0508580.
Auer, Peter; Cesa-Bianchi, Nicolò; Fischer, Paul (2002). Finite-time Analysis of the Multiarmed Bandit Problem. Machine Learning 47 (2/3): 235–256. doi:10.1023/a:1013689704352.
Bouzy, Bruno. Old-fashioned Computer Go vs Monte-Carlo Go. IEEE Symposium on Computational Intelligence and Games, April 1–5, 2007, Hilton Hawaiian Village, Honolulu, Hawaii.
Althöfer, Ingo (2012). On Board-Filling Games with Random-Turn Order and Monte Carlo Perfectness. Advances in Computer Games. Lecture Notes in Computer Science 7168. с. 258–269. ISBN 978-3-642-31865-8. doi:10.1007/978-3-642-31866-5_22.
Ramanujan, Raghuram; Sabharwal, Ashish; Selman, Bart (May 2010). On adversarial search spaces and sampling-based planning. ICAPS '10: Proceedings of the Twentieth International Conference on International Conference on Automated Planning and Scheduling: 242–245.
Ramanujan, Raghuram; Selman, Bart (March 2011). Trade-Offs in Sampling-Based Adversarial Planning. ICAPS '11: Proceedings of the International Conference on Automated Planning and Scheduling 21 (1): 202–209.
Lee Sedol defeats AlphaGo in masterful comeback - Game 4. Go Game Guru. Архів оригіналу за 16 листопада 2016. Процитовано 4 липня 2017.
Świechowski, M.; Mańdziuk, J., «Self-Adaptation of Playing Strategies in General Game Playing» (2010), IEEE Transactions on Computational Intelligence and AI in Games, vol: 6(4), pp. 367—381, doi: 10.1109/TCIAIG.2013.2275163, http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6571225&isnumber=4804729
Drake, Peter (December 2009). The Last-Good-Reply Policy for Monte-Carlo Go. ICGA Journal 32 (4): 221–227. doi:10.3233/ICG-2009-32404.
Seth Pellegrino; Peter Drake (2010). Investigating the Effects of Playout Strength in Monte-Carlo Go. Proceedings of the 2010 International Conference on Artificial Intelligence, ICAI 2010, July 12–15, 2010, Las Vegas Nevada, USA. CSREA Press. с. 1015–1018. ISBN 978-1-60132-148-0.
Gelly, Sylvain; Silver, David (2007). Combining Online and Offline Knowledge in UCT. Machine Learning, Proceedings of the Twenty-Fourth International Conference (ICML 2007), Corvallis, Oregon, USA, June 20–24, 2007. ACM. с. 273–280. ISBN 978-1-59593-793-3. Архів оригіналу|archiveurl= вимагає |url= (довідка) за 28 серпня 2017.
David Silver (2009). Reinforcement Learning and Simulation-Based Search in Computer Go. PhD thesis, University of Alberta.
Rémi Coulom. CLOP: Confident Local Optimization for Noisy Black-Box Parameter Tuning. ACG 2011: Advances in Computer Games 13 Conference, Tilburg, the Netherlands, November 20–22.
Guillaume M.J-B. Chaslot, Mark H.M. Winands, Jaap van den Herik (2008). Parallel Monte-Carlo Tree Search. Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. Springer. с. 60–71. ISBN 978-3-540-87607-6.
Markus Enzenberger; Martin Müller (2010). A Lock-free Multithreaded Monte-Carlo Tree Search Algorithm. У Jaap Van Den Herik. Advances in Computer Games: 12th International Conference, ACG 2009, Pamplona, Spain, May 11–13, 2009, Revised Papers. Springer. с. 14–20. ISBN 978-3-642-12992-6.

Бібліографія

Cameron Browne; Edward Powley; Daniel Whitehouse; Simon Lucas; Peter I. Cowling; Philipp Rohlfshagen; Stephen Tavener; Diego Perez та ін. (March 2012). A Survey of Monte Carlo Tree Search Methods. IEEE Transactions on Computational Intelligence and AI in Games 4 (1): 1–43. doi:10.1109/tciaig.2012.2186810.

Посилання

Посібник для початківців з дерева пошуку Монте-Карло

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[alphago-1] Silver, David; Huang, Aja; Maddison, Chris J.; Guez, Arthur; Sifre, Laurent; Driessche, George van den; Schrittwieser, Julian; Antonoglou, Ioannis та ін. (28 січня 2016). Mastering the game of Go with deep neural networks and tree search. Nature 529 (7587): 484–489. Bibcode:2016Natur.529..484S. ISSN 0028-0836. PMID 26819042. doi:10.1038/nature16961.

[AIAP-2] >Artificial Intelligence: A Modern Approach (вид. 3rd). Prentice Hall. 2009.

[cpr-3] Jonathan Rubin; Ian Watson (April 2011). Computer poker: A review. Artificial Intelligence 175 (5–6): 958–987. doi:10.1016/j.artint.2010.12.005. Архів оригіналу за 13 серпня 2012.

[4] Monte-Carlo Tree Search in TOTAL WAR: ROME II's Campaign AI. AI Game Dev. Архів оригіналу за 13 березня 2017. Процитовано 25 лютого 2017.

[5] Tesla's AI Day video https://youtube.com/watch?v=j0z4FweCy4M

[Abramson-6] Abramson, Bruce (1987). The Expected-Outcome Model of Two-Player Games. Technical report, Department of Computer Science, Columbia University. Процитовано 23 грудня 2013.

[7] Wolfgang Ertel; Johann Schumann; Christian Suttner (1989). Learning Heuristics for a Theorem Prover using Back Propagation.. У J. Retti. 5. Österreichische Artificial-Intelligence-Tagung. Informatik-Fachberichte 208,pp. 87-95. Springer.

[8] Christian Suttner; Wolfgang Ertel (1990). Automatic Acquisition of Search Guiding Heuristics.. CADE90, 10th Int. Conf. on Automated Deduction.pp. 470-484. LNAI 449. Springer.

[9] Christian Suttner; Wolfgang Ertel (1991). Using Back-Propagation Networks for Guiding the Search of a Theorem Prover.. Journal of Neural Networks Research & Applications 2 (1): 3–16.

[Bruegmann-10] Brügmann, Bernd (1993). Monte Carlo Go. Technical report, Department of Physics, Syracuse University.

[Chang2005-11] Chang, Hyeong Soo; Fu, Michael C.; Hu, Jiaqiao; Marcus, Steven I. (2005). An Adaptive Sampling Algorithm for Solving Markov Decision Processes. Operations Research 53: 126–139. doi:10.1287/opre.1040.0145.

[changORMStoday-12] Hyeong Soo Chang; Michael Fu; Jiaqiao Hu; Steven I. Marcus (2016). Google DeepMind's Alphago: O.R.'s unheralded role in the path-breaking achievement. OR/MS Today 45 (5): 24–29.

[13] Sensei's Library: KGSBotRatings. Процитовано 3 травня 2012.

[14] Rémi Coulom (2008). The Monte-Carlo Revolution in Go. Japanese-French Frontiers of Science Symposium.

[15] Rémi Coulom (2007). Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. Computers and Games, 5th International Conference, CG 2006, Turin, Italy, May 29–31, 2006. Revised Papers. Springer. с. 72–83. ISBN 978-3-540-75537-1.

[Kocsis-Szepesvari-16] . ISBN 3-540-45375-X. Пропущений або порожній |title= (довідка)

[Gelly-et-al-17] Sylvain Gelly; Yizao Wang; Rémi Munos; Olivier Teytaud (November 2006). Modification of UCT with Patterns in Monte-Carlo Go. Technical report, INRIA.

[18] Chang-Shing Lee; Mei-Hui Wang; Guillaume Chaslot; Jean-Baptiste Hoock; Arpad Rimmel; Olivier Teytaud; Shang-Rong Tsai; Shun-Chin Hsu та ін. (2009). The Computational Intelligence of MoGo Revealed in Taiwan's Computer Go Tournaments. IEEE Transactions on Computational Intelligence and AI in Games 1 (1): 73–89. doi:10.1109/tciaig.2009.2018703.

[19] Markus Enzenberger; Martin Mūller (2008). Fuego – An Open-Source Framework for Board Games and Go Engine Based on Monte Carlo Tree Search. Technical report, University of Alberta.

[20] The Shodan Go Bet. Процитовано 2 травня 2012.

[21] Research Blog: AlphaGo: Mastering the ancient game of Go with Machine Learning. Google Research Blog. 27 січня 2016.

[22] Google achieves AI 'breakthrough' by beating Go champion. BBC News. 27 січня 2016.

[23] Match 1 - Google DeepMind Challenge Match: Lee Sedol vs AlphaGo. Youtube. 9 березня 2016.

[24] Google AlphaGo AI clean sweeps European Go champion. ZDNet. 28 січня 2016.

[25] Broderick Arneson; Ryan Hayward; Philip Henderson (June 2009). MoHex Wins Hex Tournament. ICGA Journal 32 (2): 114–116. doi:10.3233/ICG-2009-32218.

[26] Timo Ewalds (2011). Playing and Solving Havannah. Master's thesis, University of Alberta.

[27] Richard J. Lorentz (2008). Amazons Discover Monte-Carlo. Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. Springer. с. 13–24. ISBN 978-3-540-87607-6.

[28] Tomáš Kozelek (2009). Methods of MCTS and the game Arimaa. Master's thesis, Charles University in Prague.

[29] Xiaocong Gan; Yun Bao; Zhangang Han (December 2011). Real-Time Search Method in Nondeterministic Game – Ms. Pac-Man. ICGA Journal 34 (4): 209–222. doi:10.3233/ICG-2011-34404.

[30] Tom Pepels; Mark H. M. Winands; Marc Lanctot (September 2014). Real-Time Monte Carlo Tree Search in Ms Pac-Man. IEEE Transactions on Computational Intelligence and AI in Games 6 (3): 245–257. doi:10.1109/tciaig.2013.2291577.

[31] Mountain, Gwaredd (2015). Tactical Planning and Real-time MCTS in Fable Legends. Процитовано 8 червня 2019. «.. we implemented a simulation based approach, which involved modelling the game play and using MCTS to search the potential plan space. Overall this worked well, ...»

[32] Michael Buro; Jeffrey Richard Long; Timothy Furtak; Nathan R. Sturtevant (2009). Improving State Evaluation, Inference, and Search in Trick-Based Card Games. IJCAI 2009, Proceedings of the 21st International Joint Conference on Artificial Intelligence, Pasadena, California, USA, July 11–17, 2009. с. 1407–1413.

[33] C.D. Ward; P.I. Cowling (2009). Monte Carlo Search Applied to Card Selection in Magic: The Gathering. CIG'09 Proceedings of the 5th international conference on Computational Intelligence and Games. IEEE Press. Архів оригіналу|archiveurl= вимагає |url= (довідка) за 28 травня 2016.

[34] István Szita; Guillaume Chaslot; Pieter Spronck (2010). Monte-Carlo Tree Search in Settlers of Catan. У Jaap Van Den Herik. Advances in Computer Games, 12th International Conference, ACG 2009, Pamplona, Spain, May 11–13, 2009. Revised Papers. Springer. с. 21–32. ISBN 978-3-642-12992-6.

[chaslot2008-35] G.M.J.B. Chaslot; M.H.M. Winands; J.W.H.M. Uiterwijk; H.J. van den Herik; B. Bouzy (2008). Progressive Strategies for Monte-Carlo Tree Search. New Mathematics and Natural Computation 4 (3): 343–359. doi:10.1142/s1793005708001094.

[36] Bradberry, Jeff (7 вересня 2015). Introduction to Monte Carlo Tree Search.

[37] Peres, Yuval (2006). «Random-Turn Hex and other selection games». arXiv:abs/math/0508580.

[38] Auer, Peter; Cesa-Bianchi, Nicolò; Fischer, Paul (2002). Finite-time Analysis of the Multiarmed Bandit Problem. Machine Learning 47 (2/3): 235–256. doi:10.1023/a:1013689704352.

[39] Bouzy, Bruno. Old-fashioned Computer Go vs Monte-Carlo Go. IEEE Symposium on Computational Intelligence and Games, April 1–5, 2007, Hilton Hawaiian Village, Honolulu, Hawaii.

[40] Althöfer, Ingo (2012). On Board-Filling Games with Random-Turn Order and Monte Carlo Perfectness. Advances in Computer Games. Lecture Notes in Computer Science 7168. с. 258–269. ISBN 978-3-642-31865-8. doi:10.1007/978-3-642-31866-5_22.

[41] Ramanujan, Raghuram; Sabharwal, Ashish; Selman, Bart (May 2010). On adversarial search spaces and sampling-based planning. ICAPS '10: Proceedings of the Twentieth International Conference on International Conference on Automated Planning and Scheduling: 242–245.

[42] Ramanujan, Raghuram; Selman, Bart (March 2011). Trade-Offs in Sampling-Based Adversarial Planning. ICAPS '11: Proceedings of the International Conference on Automated Planning and Scheduling 21 (1): 202–209.

[43] Lee Sedol defeats AlphaGo in masterful comeback - Game 4. Go Game Guru. Архів оригіналу за 16 листопада 2016. Процитовано 4 липня 2017.

[44] Świechowski, M.; Mańdziuk, J., «Self-Adaptation of Playing Strategies in General Game Playing» (2010), IEEE Transactions on Computational Intelligence and AI in Games, vol: 6(4), pp. 367—381, doi: 10.1109/TCIAIG.2013.2275163, http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6571225&isnumber=4804729

[45] Drake, Peter (December 2009). The Last-Good-Reply Policy for Monte-Carlo Go. ICGA Journal 32 (4): 221–227. doi:10.3233/ICG-2009-32404.

[46] Seth Pellegrino; Peter Drake (2010). Investigating the Effects of Playout Strength in Monte-Carlo Go. Proceedings of the 2010 International Conference on Artificial Intelligence, ICAI 2010, July 12–15, 2010, Las Vegas Nevada, USA. CSREA Press. с. 1015–1018. ISBN 978-1-60132-148-0.

[Gelly-Silver-47] Gelly, Sylvain; Silver, David (2007). Combining Online and Offline Knowledge in UCT. Machine Learning, Proceedings of the Twenty-Fourth International Conference (ICML 2007), Corvallis, Oregon, USA, June 20–24, 2007. ACM. с. 273–280. ISBN 978-1-59593-793-3. Архів оригіналу|archiveurl= вимагає |url= (довідка) за 28 серпня 2017.

[48] David Silver (2009). Reinforcement Learning and Simulation-Based Search in Computer Go. PhD thesis, University of Alberta.

[49] Rémi Coulom. CLOP: Confident Local Optimization for Noisy Black-Box Parameter Tuning. ACG 2011: Advances in Computer Games 13 Conference, Tilburg, the Netherlands, November 20–22.

[50] Guillaume M.J-B. Chaslot, Mark H.M. Winands, Jaap van den Herik (2008). Parallel Monte-Carlo Tree Search. Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. Springer. с. 60–71. ISBN 978-3-540-87607-6.

[51] Markus Enzenberger; Martin Müller (2010). A Lock-free Multithreaded Monte-Carlo Tree Search Algorithm. У Jaap Van Den Herik. Advances in Computer Games: 12th International Conference, ACG 2009, Pamplona, Spain, May 11–13, 2009, Revised Papers. Springer. с. 14–20. ISBN 978-3-642-12992-6.