Експонента (теорія груп Лі)

Нехай ${\displaystyle G}$ — група Лі, а ${\displaystyle {\mathfrak {g}}}$ — відповідна алгебра Лі. Алгебру Лі можна інтерпретувати, як дотичний простір в одиниці групи, тобто ${\displaystyle T_{e}G}$ або як простір лівоінваріантних векторних полів на групі ${\displaystyle G.}$ Таке лівоінваріантне векторне поле значення якого на одиничному елементі рівне ${\displaystyle X}$ позначається ${\displaystyle v_{X}.}$

Оскільки група Лі є гладким многовидом для векторного поля ${\displaystyle v_{X}}$ в околі одиничного елемента існує інтегральна крива ${\displaystyle \gamma _{X}(t)}$ така що ${\displaystyle \gamma _{X}(0)=e.}$ Неважко довести, що для груп Лі дана інтегральна крива визначена для всіх дійсних чисел і ${\displaystyle \gamma _{X}(s+t)=\gamma _{X}(s)\gamma _{X}(t).}$

Тому можна визначити відображення ${\displaystyle \exp \colon {\mathfrak {g}}\to G}$ визначене як:

${\displaystyle \exp(X)=\gamma _{X}(1).}$

Це відображення і називається екпоненційним відображенням або експонентою.

• Позначивши ${\displaystyle \mathbb {R} _{+}}$ — множину додатних дійсних чисел з операцією множення отримаємо групу Лі алгебра Лі якої ізоморфна множині дійсних чисел. Експонента в цьому випадку рівна звичайній експоненті дійсних чисел.
• Нехай ${\displaystyle GL(n,\mathbb {R} )}$ — множина невироджених дійсних матриць розмірності n. Разом з операцією множення матриць ця множина є групою Лі алгебра Лі якої рівна ${\displaystyle M(n,\mathbb {R} )}$ — множина квадратних матриць розмірності n. Експонентою в цьому випадку буде експонента матриць.
• Нехай V — скінченновимірний дійсний лінійний простір, який з операцією додавання векторів є групою Лі. Тоді ${\displaystyle \operatorname {Lie} (V)=V}$ через ідентифікацію простору V з його дотичним простором у точці 0. При такій ідентифікації експонента

${\displaystyle \operatorname {exp}$ :\operatorname {Lie} (V)=V\to V}

є тотожним відображенням.

• Якщо ${\displaystyle t,s\in \mathbb {R} ,}$ то ${\displaystyle \exp tX=\gamma _{tX}(1)=\gamma _{X}(t)}$ звідки з властивостей цих кривих ${\displaystyle \exp(t+s)X=(\exp tX)(\exp sX).}$
• Як наслідок з попереднього ${\displaystyle \exp(-X)=(\exp X)^{-1}.\,}$
• Експоненційне відображення ${\displaystyle \exp \colon {\mathfrak {g}}\to G}$ є гладким відображенням. Його диференціал у нулі, ${\displaystyle \exp _{*}\colon {\mathfrak {g}}\to {\mathfrak {g}}}$, є тотожним лінійним відображенням. Відповідно експонента є дифеоморфізмом між деяким околом 0 в ${\displaystyle {\mathfrak {g}}}$ і деяким околом одиничного елемента в групі ${\displaystyle G}$.

• Загалом проте експонента не є локальним дифеоморфізмом в кожній своїй точці, прикладом може бути відображення з so(3) в SO(3).
• ${\displaystyle \exp tX}$ є однопараметричною підгрупою в ${\displaystyle G,}$ тобто гладким гомоморфізмом х групи ${\displaystyle \mathbb {R} }$ з операцією додавання в групу ${\displaystyle G.}$ Більш того всі однопараметричні підгрупи в ${\displaystyle G}$ мають вигляд ${\displaystyle \exp tX}$ для деякого ${\displaystyle X\in {\mathfrak {g}}.}$
• Нехай ${\displaystyle \phi \colon G\to H}$ — гомоморфізм груп Лі і ${\displaystyle \phi _{*}}$ його диференціал в одиниці. Тоді наступна діаграма є комутуючою:

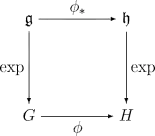
• Застосовуючи попередню властивість до приєднаних представлень групи ${\displaystyle G}$ отримуємо властивості:
  • ${\displaystyle g(\exp X)g^{-1}=\exp(\mathrm {Ad} _{g}X)\,}$
  • ${\displaystyle \mathrm {Ad} _{\exp X}=\exp(\mathrm {ad} _{X}).\,}$
• Нехай елементи ${\displaystyle X,Y\in {\mathfrak {g}}}$ комутують, тобто ${\displaystyle [X,Y]=0,}$ тоді елементи ${\displaystyle \exp X,\exp Y}$ комутують, як елементи групи ${\displaystyle G}$ щодо операції множення в групі й крім того ${\displaystyle \exp(X+Y)=\exp X\exp Y.}$
• Позначивши ${\displaystyle G_{e}}$ — зв'язану компоненту групи ${\displaystyle G,}$ що містить одиничний елемент (${\displaystyle G_{e}}$ є підгрупою в ${\displaystyle G}$) то множина ${\displaystyle {\exp X,\;X\in {\mathfrak {g}}}}$ є породжуючою для ${\displaystyle G_{e},}$ тобто довільний елемент ${\displaystyle g\in G_{e}}$ можна записати як ${\displaystyle \exp X_{1}\cdot \exp X_{2}\cdot \ldots \cdot \exp X_{n},}$ де ${\displaystyle X_{1},\ldots ,X_{n}\in {\mathfrak {g}}.}$ Зокрема група Лі є зв'язаною тоді й лише тоді коли всі її елементи можна записати в такому виді.
• Якщо група ${\displaystyle G}$ є компактною або нільпотентною то експоненційне відображення є сюрєкцією на ${\displaystyle G_{e},}$ тобто довільний елемент ${\displaystyle g\in G_{e}}$ рівний ${\displaystyle \exp X}$ для деякого ${\displaystyle X\in {\mathfrak {g}}.}$ Це ж твердження справедливе і у випадку групи ${\displaystyle GL(n,\mathbb {R} ).}$
• Образ експоненційного відображення у зв'язаній але не компактній чи нільпотентній групі ${\displaystyle SL(2,\mathbb {R} )}$ не рівний усій групі. Образом може бути ${\displaystyle \mathbb {C} }$ -діагоналізовна матриця з власними значеннями рівними додатнім дійсним числам чи недійсним числам з модулем 1, недіагоналізовні матриці обидва власні значення яких рівні 1 і матриця ${\displaystyle -I}$. Зокрема матриці з дійсними від'ємними власними значеннями за виключенням ${\displaystyle -I}$ не належать образу. [1]

• Приєднане представлення групи Лі
• Експонента матриці
• Експоненційне відображення

• E.P. van den Ban Lecture Notes on Lie groups

• Голод П. І., Клімик А. У. Математичні основи теорії симетрії. — К. : Наукова думка, 1992. — 368 с.
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics 222 (вид. 2nd). Springer. ISBN 0-387-40122-9..
• Hazewinkel, Michiel, ред. (2001). Exponential mapping. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
• Helgason, Sigurdur (2001). Differential geometry, Lie groups, and symmetric spaces. Graduate Studies in Mathematics 34. Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-2848-9. MR 1834454..
• Kobayashi, Shoshichi; Nomizu, Katsumi (1996). Foundations of Differential Geometry. Vol. 1 (вид. New). Wiley-Interscience. ISBN 0-471-15733-3..