Диференціал (математика)

Диференціал в математиці — головна, лінійна відносно приросту аргументу, частина приросту функції або відображення.

Приріст та лінійна частина приросту функції однієї змінної

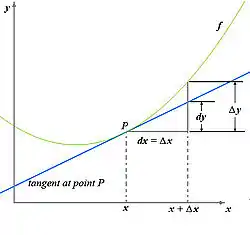
В математичному аналізі диференціал традиційно вважається нескінченно малим приростом змінної. Наприклад, якщо x — змінна, тоді приріст значення x часто позначається Δx (чи δx, якщо цей приріст малий). Диференціал dx також є таким приростом, але нескінченно малим. Варто зазначити, що таке визначення не є математично строгим, але воно зручне для розуміння, також існує багато способів зробити визначення математично точнішим.

Головна властивість диференціалу: якщо y функція від x, тоді диференціал dy від y пов'язаний з dx формулою:

\mathrm {d} y={\frac {\mathrm {d} y}{\mathrm {d} x}}\,\mathrm {d} x,

де dy/dx позначає похідну від y по змінній x. Ця формула підсумовує інтуїтивне твердження, що похідна y по змінній x це границя відношення приростів Δy/Δx де Δx прямує до нуля.

Диференціал як лінійне відображення. Цей підхід є основою визначення повної похідної і зовнішньої похідної в диференціальній геометрії.[1]
Диференціал як нільпотентний елемент в комутативних кільцях. Такий підхід популярний в алгебраїчній геометрії.[2]

Ці підходи дуже різні, але їх об'єднує ідея кількісного, тобто важливо сказати, що диференціал не тільки нескінченно малий, а наскільки саме він малий.

Історія і використання

Нескінченно малі величини грали значну роль в розвитку математичного аналізу. Архімед використовував їх, хоча він і не вірив, що твердження з нескінченно малими величинами можуть бути точні.[3] Бхаскара II розробив концепцію диференціального відображення нескінченно малих змін.[4] Шараф аль-Дін аль-Тусі використовував їх для обчислення похідної кубічного рівняння.[5][6] Ісаак Ньютон називав їх похідними. Проте Лейбніц був перший хто застосував термін диференціал до нескінченно малих величин, а також придумав позначення похідної, яке використовується дотепер.

В позначенні Лейбніца, якщо x — змінне число тоді dx позначає нескінченно малий приріст змінної x. Таким чином, якщо y функція від x, тоді похідна y по змінній x часто позначається ${\frac {\mathrm {d} y}{\mathrm {d} x}}$ , що також може бути записано (позначення Ньютона чи Лагранжа) ${\dot {y}}(x)$ чи $y'(x)$ . Використання диференціалів в такій формі спровокувало багато критики, наприклад знаменитий памфлет The Analyst єпископа Берклі. В будь-якому разі таке позначення залишилось популярним, тому що воно наочно відображає принцип, що похідна функції y(x) дорівнює нахилу функції в точці, що можна отримати, якщо обчислити границю відношення ${\frac {\Delta \,y}{\Delta \,x}}$ приросту y в залежності від приросту x, якщо приріст x прямує до нуля. Диференціали також застосовують в аналізі розмірності, де диференціал наприклад dx маю таку саму розмірність як і змінна x.

Сума Рімана є певного виду наближенням інтегралу за допомогою скінченної суми. Вона названа на честь німецького математика із дев'ятнадцятого століття Бернгарда Рімана. Його одним із самих загальних застосувань є апроксимація площі, що обмежують графіки функцій або криві, а також довжини кривих і інші наближення.

Диференціал використовують в позначенні інтеграла, тому що інтеграл можна вважати нескінченною сумою нескінченно малих величин: площа під графіком функції обчислюється як сума площ нескінченно тонких стрічок. У виразі

\int f(x)\,{\mathrm {d} }x,

знак інтеграла (витягнуте s) означає нескінченну суму, f(x) позначає 'висоту' тонкої стрічки, а диференціал dx позначає нескінченно тонку ширину.

Формальні означення

Об'єм кубу - функція від довжини його сторони, $V=x^{3}.$ За рахунок лінійного термічного розширення сторони кубу збільшуються, а тому збільшується й його об'єм. Якщо довжина сторони куба мала значення $x$ й збільшилася на $h,$ то вона прийме значення $x+h$ і об'єм куба стане рівним $(x+h)^{3}.$ Величина, на яку збільшиться його об'єм, буде складати $(x+h)^{3}-x^{3}.$ Цю різницю називають прирощенням об'му куба, а число $h$ , яке показує, на скільки збільшилася довжина строни куба, називається прирощенням його довжини. У математиці прирощення якої-небудь величини позначається $\Delta x,$ де $\Delta$ - велика грецька літера "дельта", яка нагадує про латинське слово differentia - "різниця".

Якщо функція

y=f(x)

зростає на відрізку

[a;\,b],

то на цьому відрізку знаки

\Delta y

та

\Delta x

співпадають - при збільшенні

x

збільшується й

y,

а при зменшенні

x

зменшується й

y

(графік ліворуч на малюнку). Якщо ж функція

y=f(x)

спадає на цьому відрізку, то у будь-якій його точці знаки

\Delta x

та

\Delta y

протилежні.

Якщо $y=f(x)$ - декотра функція й $x$ прирощується, $\Delta x,$ то змінюється й значення функції, в результаті чого вона отримує деяке прирощення $\Delta y.$ Щоб обчислити це прирощення, необхідно:

знайти значення функції при початковому значенні аргумента, тобто $y=f(x)$ ;
знайти нове значення аргумента, тобто $x+\Delta x$ ;
знайти нове значення функції, тобто $f(x+\Delta x)$ ;
з нового значення функції відняти початкове її значення,тобто $\Delta y=f(x+\Delta x)-f(x).$

Наприклад, прирощення функції $y=x^{3}$ має вигляд $\Delta y=3x^{2}\Delta x+3x\Delta x^{2}+\Delta x^{3};$ це прирощення можна записати наступним чином: $\Delta y=3x^{2}\Delta x+(3x\Delta x+\Delta x^{2})\Delta x.$ Воно складається з двох доданків $3x^{2}\Delta x$ та $[3x\Delta x+(\Delta x)^{2}]\Delta x.$ Перший доданок пропорційний прирощенню аргументу $\Delta x.$ Другий доданок складніший, залежить від $\Delta x.$ Але за малих $\Delta x$ він набагато менший, ніж $3x^{2}\Delta x,$ тому що є добутком $\Delta x$ на вираз $3x\Delta x+(\Delta x)^{2},$ який прагне до нуля за $\Delta x\to 0.$

$x=1$
$\Delta x$	$\Delta y$	$3x^{2}\Delta x$	$[3x\Delta x+(\Delta x)^{2}]\Delta x$
0,1	0,331	0,3	0,031
0,01	0,030301	0,03	0,000301
0,001	0,003003001	0,003	0,000003001

Таким чином, доданок $3x^{2}\Delta x$ , який є пропорційним $\Delta x$ , за малих значеннях $\Delta x$ є головною частиною прирощення функції. Такий доданок називається диференціалом й позначається $dy=3x^{2}\Delta x.$ Він залежить не лише від $\Delta x$ , але й від $x.$ Наприклад, для функції $y=x^{3}$ при $x=1$ та $\Delta x=0,1$ він дорівнює $dy=1,2.$ У випадку $\Delta x=0,01$ та $x=1$ диференціал $dy=0,03.$

Диференціал функції

S=x^{2}.

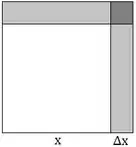
Прирощення функції $y=x^{2}$ має вигляд $\Delta y=(x+\Delta x)^{2}-x^{2}=2x\Delta x+(\Delta x)^{2}.$ Доданком, пропорційним $\Delta x,$ є $2x\Delta x.$ Цей доданок і є диференціалом заданої функції: $dy=2x\Delta x=2x\,dx.$ Формула для диференціалу $y=x^{2}$ має простий геометричний сенс. Оскільки $S=x^{2}$ - площина квадрату, сторона якого має довжину $x,$ то $\Delta S$ - площина фігури, на яку її площа збільшується. Зрозуміло, що за малих $\Delta x$ головну частину цієї площини складає площина двох прямокутників, яка дорівнює $2x\Delta x,$ тобто диференціалу функції $S=x^{2}.$ Вираз $(\Delta x)^{2}$ - площина квадратику, яка нескінченно мала у порівнянні із $\Delta x.$

Випадок однієї змінної

Нехай в околі точки $x_{0}$ задана функція $f(x):X\rightarrow Y$ .

нехай існує таке $A$ , що $f(x)-f(x_{0})=A(x-x_{0})+o(x-x_{0})$ при $x\rightarrow x_{0}$ .

Позначимо $x-x_{0}=dx$ .

Тоді функція $df=Adx$ називається диференціалом функції $f(x)$ в точці $x_{0}$ .

Випадок багатьох змінних

Приклад 1. Нехай в околі точки ${\overrightarrow {x_{0}}}=\{x_{0}^{1},x_{0}^{2},...,x_{0}^{n}\}$ задана функція багатьох змінних $f({\overrightarrow {x}}):X\rightarrow Y$ .

Нехай існує такий вектор ${\overrightarrow {A}}=\{A^{1},A^{2},...,A^{n}\}$ , що $f({\overrightarrow {x}})-f({\overrightarrow {x_{0}}})={\overrightarrow {A}}({\overrightarrow {x}}-{\overrightarrow {x_{0}}})+o({\overrightarrow {x}}-{\overrightarrow {x_{0}}})$ при ${\overrightarrow {x}}\rightarrow {\overrightarrow {x_{0}}}$ , де добуток векторів є скалярним добутком.

Позначимо ${\overrightarrow {x}}-{\overrightarrow {x_{0}}}={\overrightarrow {dx}}=\{{dx}^{1},{dx}^{2},...,{dx}^{n}\}$ .

Тоді функція $df={\overrightarrow {A}}{\overrightarrow {dx}}$ називатиметься диференціалом функції $f({\overrightarrow {x}})$ в точці ${\overrightarrow {x_{0}}}$ .

Приклад 2. Тепер нехай $\Delta f=f(x_{1}+\Delta x_{1},x_{2}+\Delta x_{2},...,x_{n}+\Delta x_{n})-f(x_{1},x_{2},...,x_{n}),$ приріст функції $f(x_{1},x_{2},...,x_{n}).$ Неперервність частинних похідних ${\frac {\partial f}{\partial x_{i}}}$ є умовою, достатньою для існування диференціалу. У цьому випадку

$\Delta f=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}\Delta x_{i}+R_{1},$

де $R$ нескінченно мале у порівнянні із ${\sqrt {\Delta x_{1}^{2}+\Delta x_{2}^{2}+...+\Delta x_{n}^{2}}}.$ Вираз $df=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}\Delta x_{i}$ є диференціалом функції багатьох змінних.

Відображення між евклідовими просторами

Диференціал відображення - головна, лінійна відносно приросту аргументу, частина відображеня, яка задається деякою матрицею. Також поняття диференціала можна ввести для відображення між евклідовими просторами ƒ Rⁿ → R^m. Нехай x,Δx ∈ Rⁿ — два вектори в просторі Rⁿ. Зміна значення функції ƒ при зміні аргументу на Δx рівна:

\Delta f=f(\mathbf {x} +\Delta \mathbf {x} )-f(\mathbf {x} ).

Якщо існує m × n матриця A для якої

\Delta f=A\Delta \mathbf {x} +\|\Delta \mathbf {x} \|{\boldsymbol {\varepsilon }}

де вектор ε → 0 при Δx → 0, тоді ƒ називається диференційовною в точці x. Матриця A називається матрицею Якобі, а лінійне перетворення, що ставить у відповідності вектору Δx ∈ Rⁿ вектор AΔx ∈ R^m називається диференціалом dƒ(x) відображення ƒ в точці x.

Відображення між многовидами

Диференціал в точці $x\in M$ гладкого відображення із гладкого многовиду в многовид $F\colon M\to N$ визначається як лінійне відображення між дотичними просторами в точках $x\in M$ і $F(x)\in N,$ тобто $dF\colon T_{x}M\to T_{F(x)}N,$ таке що для довільної гладкої в точці F(x) функції $g\colon N\to \mathbb {R}$ виконується рівність:

dF(X)g=X(g\circ F),\quad \forall X\in T_{x}M.

Примітки

Darling, R. W. R. (1994). Differential forms and connections. Cambridge, UK: Cambridge University Press. ISBN 0-521-46800-0.
Eisenbud, David; Harris, Joe (1998). The Geometry of Schemes. Springer-Verlag. ISBN 0-387-98637-5.
Boyer, Carl B. (1991). Archimedes of Syracuse. A History of Mathematics (вид. 2nd). John Wiley & Sons, Inc. ISBN 0471543977.
George G. Joseph (2000), The Crest of the Peacock, pp. 298–300, Princeton University Press, ISBN 0-691-00659-8
J. L. Berggren (1990), «Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat», Journal of the American Oriental Society 110 (2): 304-9
Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Sharaf al-Din al-Muzaffar al-Tusi в архіві MacTutor (англ.)

Література

С. Т. Завало (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа.
Хемминг Р.В. - Численные методы для научных работников и инженеров (2-е издание) - 1972

Посилання

Диференціал функції // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 266. — 594 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Darling, R. W. R. (1994). Differential forms and connections. Cambridge, UK: Cambridge University Press. ISBN 0-521-46800-0.

[2] Eisenbud, David; Harris, Joe (1998). The Geometry of Schemes. Springer-Verlag. ISBN 0-387-98637-5.

[3] Boyer, Carl B. (1991). Archimedes of Syracuse. A History of Mathematics (вид. 2nd). John Wiley & Sons, Inc. ISBN 0471543977.

[Joseph-4] George G. Joseph (2000), The Crest of the Peacock, pp. 298–300, Princeton University Press, ISBN 0-691-00659-8

[5] J. L. Berggren (1990), «Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat», Journal of the American Oriental Society 110 (2): 304-9

[MacTutor-6] Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Sharaf al-Din al-Muzaffar al-Tusi в архіві MacTutor (англ.)