Інтегральна крива

У математиці, інтегральна крива (англ. integral curve) — параметрична крива, що представляє певний розв'язок для звичайного диференціального рівняння або системи рівнянь. Якщо диференціальне рівняння представлене як векторне поле або поле напрямків, тоді відповідна інтегральна крива дотична до поля в кожній точці.

Три інтегральні криви для поля напрямків відповідного диференціальному рівнянню dy / dx = x² − x − 1.

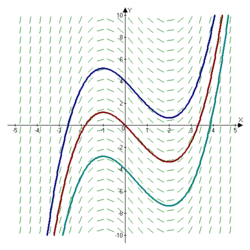
Інтегральні криві також відомі під іншими назвами, залежно від природи і тлумачення диференціального рівняння або векторного поля. У фізиці, інтегральна крива для електричного або магнітного поля відома як силова лінія, інтегральна крива для поля швидкостей флюїду відома як лінія потоку. В динамічних системах, інтегральна крива для диференціального рівняння, яке керує системою згадується як траєкторія або орбіта.

Визначення

Припустимо, що F — векторне поле: тобто, вектор-функція з декартовими координатами (F₁,F₂,...,F_n); і x(t) парметрична крива з координатами (x₁(t),x₂(t),...,x_n(t)). Тодіx(t) — це інтегральна крива F якщо вона є розв'язком такої автономної системи звичайних диференціальних рівнянь:

{\begin{aligned}{\frac {dx_{1}}{dt}}&=F_{1}(x_{1},\ldots ,x_{n})\\&\vdots \\{\frac {dx_{n}}{dt}}&=F_{n}(x_{1},\ldots ,x_{n}).\end{aligned}}

Таку систему можна записати як одне векторне рівняння

\mathbf {x} '(t)=\mathbf {F} (\mathbf {x} (t)).\!\,

Таке рівняння каже, що дотичний вектор до цієї кривої в будь-якій точці x(t) уздовж кривої є саме вектором F(x(t)), і отже ця крива x(t) є в кожній точці дотичною до векторного поля F.

Див. також

Література

Самойленко А. М.; Перестюк М. О.; Парасюк I.О. (2003 р.). Диференціальні рівняння. Київ: Либідь. ISBN 966-06-0249-9. Архів оригіналу за 17 червня 2014. Процитовано 2 грудня 2015.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.