Ефект Хонга–Оу–Мендела

Коли фотон потрапляє в дільник променя, існує дві можливості: він буде або відбитим, або переданим. Відносні ймовірності пропускання та відбиття визначаються відбивною здатністю дільника променя. Тут ми припускаємо дільник променя 1:1, в якому фотон має рівну ймовірність відбиття та передачі.

Далі розглянемо два фотони, по одному в кожній вхідній моді (вхідному порті) дільника променя 1:1. Існує чотири можливості поведінки фотонів:

1. Фотон, що надходить зверху, відбивається, а фотон, що надходить знизу, передається.
2. Передаються обидва фотони.
3. Обидва фотони відбиваються.
4. Фотон, що надходить зверху, передається, а фотон, що надходить знизу, відбивається.

Тепер ми припускаємо, що два фотони однакові за своїми фізичними властивостями (тобто поляризація, просторово-часова структура мод та частота).

Чотири можливості додавання рівнів амплітуди для двофотонного відбиття та пропускання.

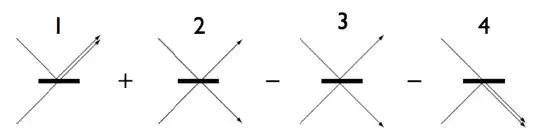
Оскільки стан роздільника променя не «фіксує», яка з чотирьох можливостей насправді трапляється, правила Фейнмана диктують, що ми повинні скласти всі чотири можливості на рівні амплітуд ймовірності. Крім того, відбиття від нижньої сторони дільника променя вводить відносний зсув фази π, що відповідає коефіцієнту -1 в асоційованому члені в суперпозиції. Цього вимагає оборотність (або унітарність) квантової еволюції дільника променя. Оскільки два фотони однакові, ми не можемо розрізнити вихідні стани можливостей 2 і 3, а їх відносний знак мінус гарантує, що ці два доданки скасуються. Це можна трактувати як руйнівну інтерференцію.

Розглянемо дві оптичні моди a і b , які несуть оператори народження та знищення ${\displaystyle {\hat {a}}}$, ${\displaystyle {\hat {a}}^{\dagger }}$, та ${\displaystyle {\hat {b}}}$, ${\displaystyle {\hat {b}}^{\dagger }}$. Два однакові фотони в різних модах можуть бути описані за допомогою станів Фока

${\displaystyle {\hat {a}}^{\dagger }{\hat {b}}^{\dagger }|0,0\rangle _{ab}=|1,1\rangle _{ab},}$

де ${\displaystyle |1\rangle }$ є однофотонним станом. Коли дві моди a і b змішані в дільнику променя 1:1, вони перетворюються на нові моди c і d, і оператори народження та знищення відповідно трансформуються:

${\displaystyle {\hat {a}}^{\dagger }\to {\frac {{\hat {c}}^{\dagger }+{\hat {d}}^{\dagger }}{\sqrt {2}}}\quad {\text{та}}\quad {\hat {b}}^{\dagger }\to {\frac {{\hat {c}}^{\dagger }-{\hat {d}}^{\dagger }}{\sqrt {2}}}.}$

Знак мінуса з'являється, оскільки дільник променя є унітарним перетворенням. Це можна зрозуміти найбільш чітко, коли двомодове перетворення дільника променя описано у формі матриці:

${\displaystyle {\begin{pmatrix}{\hat {a}}\\{\hat {b}}\end{pmatrix}}\to {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1&1\\1&-1\end{pmatrix}}{\begin{pmatrix}{\hat {c}}\\{\hat {d}}\end{pmatrix}}.}$

Унітарність перетворення тепер означає унітарність матриці. Фізично це перетворення дільника променя означає, що відбиття від однієї поверхні викликає відносний зсув фази π, що відповідає коефіцієнту -1, щодо відбиття від іншої сторони дільника променя (див. фізичний опис вище). Подібні перетворення справедливі для операторів анігіляції.

Коли два фотони потрапляють в дільник променя, по одному з кожного боку, стан двох мод стає

${\displaystyle |1,1\rangle _{ab}={\hat {a}}^{\dagger }{\hat {b}}^{\dagger }|0,0\rangle _{ab}\to {\frac {1}{2}}\left({\hat {c}}^{\dagger }+{\hat {d}}^{\dagger }\right)\left({\hat {c}}^{\dagger }-{\hat {d}}^{\dagger }\right)|0,0\rangle _{cd}={\frac {1}{2}}\left({\hat {c}}^{\dagger 2}-{\hat {d}}^{\dagger 2}\right)|0,0\rangle _{cd}={\frac {|2,0\rangle _{cd}-|0,2\rangle _{cd}}{\sqrt {2}}}.}$

Так як комутатор двох операторів створення ${\displaystyle {\hat {c}}^{\dagger }}$ і ${\displaystyle {\hat {d}}^{\dagger }}$ зникає, в суперпозиції зберігаються терми є ${\displaystyle {\hat {c}}^{\dagger 2}}$ і ${\displaystyle {\hat {d}}^{\dagger 2}}$. Отже, коли два однакові фотони потрапляють у дільник променя 1:1, вони завжди виходять із дільника променя в тій же (але випадковій) вихідній моді.

«Провал ХОМ» випадкового підрахунку в детекторах проти відносної затримки між однофотонними хвильовими пакетами

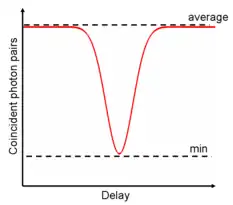
Зазвичай ефект Хонга–Оу–Мендела спостерігається за допомогою двох фотоприймачів, що контролюють вихідні моди (порти) дільника променя. Частота збігів детекторів впаде до нуля, коли однакові вхідні фотони ідеально збігаються в часі. Це називається провал Хонга–Оу–Мендела або провал ХОМ. Кількість збігів досягає мінімуму, позначеного пунктиром. Мінімум падає до нуля, коли два фотони абсолютно однакові за всіма властивостями. Коли ці два фотони можна повністю розрізнити, падіння повністю зникає. Точна форма провалу безпосередньо пов'язана з спектральною густиною однофотонного хвильового пакета і, отже, визначається фізичним процесом джерела. Загальними формами провалу ХОМ є Гауссіана та розподіл Коші — Лоренца.

Класичний аналог ефекту ХОМ виникає, коли два когерентних стани (наприклад, лазерні промені) впливають на дільник пучка. Якщо стани мають різну різницю фаз, що швидко змінюється (тобто швидше, ніж час інтегрування детекторів), тоді спостерігатиметься падіння у швидкості збігів, що дорівнює половині середнього числа збігів при великих затримках. (Тим не менше, його можна додатково зменшити за допомогою належного розрізнення рівня спрацьовування, що застосовується до сигналу.) Отже, щоб довести, що руйнівна інтерференція є двофотонною квантовою інтерференцією, а не класичним ефектом, провал ХОМ має бути меншим ніж половина.

Ефект Хонга–Оу–Мендела можна безпосередньо спостерігати за допомогою однофотонних чутливих посилених камер. Такі камери мають можливість реєструвати поодинокі фотони як яскраві плями, які чітко відрізняються від малошумного фону.

Безпосереднє спостереження ефекту ХОМ за допомогою посиленої камери. Співпалі пари фотонів з'являються разом як яскраві плями в одному з вихідних портів дільника променя (ліва або права панель).[3]

На малюнку вище пари фотонів зареєстровані в середині провалу Хонга-Оу-Мандела.[3] У більшості випадків вони виглядають згрупованими по парах зліва чи справа, що відповідає двом вихідним портам роздільника променя. Іноді трапляється випадкові події співпадіння появи фотонів на різних панелях, що виявляють залишкову відмінність між фотонами.

В експериментах виявлено ефект трифотонної інтерференції.[12][13][14]