Дільник променя
Дільник променя — це оптичний пристрій, який розділяє промінь світла навпіл. Це найважливіша частина багатьох оптичних експериментальних та вимірювальних систем, таких як інтерферометри, яка також знаходить широке застосування в оптоволоконних комунікаціях.[1]
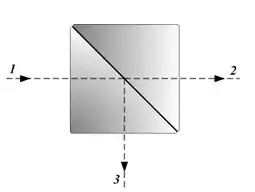
1 — Падаюче світло
2 — 50 % пропущеного світла
3 — 50 % відбитого світла
На практиці відбиваючий шар поглинає деяку частину світла.

Конструкції дільників променя
У своїй найпоширенішій формі, куб, він виготовлений із двох трикутних скляних скляних призм, які склеєні між собою за допомогою поліефірних, епоксидних клеїв або клеїв на основі уретану. Товщина шару смоли регулюється таким чином, що (для певної довжини хвилі) половина світла, що падає через один «порт» (тобто грань куба), відбивається, а інша половина передається завдяки явищу порушеного повного внутрішнього відбиття. Поляризуючі дільники променя, такі як призма Волластона, використовують матеріали з подвійним променезаломленням, щоб розділити світло на два промені з ортогональними поляризаціями.

Ще одна конструкція — використання напівпосрібленого дзеркала. Воно складається з оптичної основи, яка часто є листом скла або пластику, з частково прозорим тонким покриттям з металу. Тонке покриття може бути алюмінієм, нанесеним з пари алюмінію за допомогою методу вакуумного напилення. Товщину осаду контролюють так, щоб частина (зазвичай половина) світла, яке падає під кутом 45 градусів, не поглиналося покриттям або матеріалом підкладки, передавалась, а решта відбивалась. Дуже тонке напівпосріблене дзеркало, яке використовується у фотографії, часто називають пелікулярним дзеркалом. Для зменшення втрат світла внаслідок поглинання відбиваючим покриттям використовуються так звані дзеркала для розщеплення променя типу «швейцарський сир». Спочатку це були листи високошліфованого металу, перфоровані отворами для отримання бажаного відношення відбиття до пропускання. Пізніше метал наносили на скло розпиленням, щоб утворити неперервне покриття, або невеликі ділянки суцільного покриття видаляли хімічним або механічним впливом, отримуючи буквально «напівпосріблену» поверхню.
Замість металевого покриття може бути використано дихроїчне оптичне покриття. Залежно від його характеристик, відношення відбиття до пропускання буде змінюватися в залежності від довжини хвилі падаючого світла. Дихроїчні дзеркала використовуються в деяких еліпсоїдальних рефлекторах, щоб відділити небажане інфрачервоне (теплове) випромінювання, і як вихідний зпарювач в конструкціях лазерів.
Третя версія дільника променя — це дихроїчна дзеркальна призма, яка використовує дихроїчне оптичне покриття, щоб розділити вхідний промінь світла на ряд спектрально різних вихідних променів. Такий пристрій було використано у кольоровій телевізійній камері і триплівковій кінокамері Техніколор. У даний час він використовується в сучасних камерах з трьома матрицями. Оптично схожа система використовується в зворотному порядку для комбінування променя у трьох-LCD проекторах, в яких світло від трьох окремих монохромних рідкокристалічних дисплеїв поєднується в одне повнокольорове зображення для проектування.
Дільники променя з одномодовим волокном для мережі PON використовують одномодову поведінку для розділення променя. Дільник виконується шляхом фізичного зрощування двох волокон «разом» у формі літери «X».
Компонування дзеркал або призм, що використовуються в якості додатків для камери для фотографування стереоскопічних пар зображень з однією лінзою та однією експозицією, іноді називають «дільниками променя», але це помилкова назва, оскільки вони фактично є парою перископів, що переспрямовують промені світла, які вже не збігалися. У деяких дуже рідкісних кріпленнях для стереоскопічної фотографії дзеркала або призматичні блоки, подібні до дільників променів, виконують протилежну функцію, накладаючи види об'єкта з двох різних ракурсів за допомогою кольорових фільтрів, щоб забезпечити пряме створення анагліф 3D зображення, або через жалюзі, що швидко чергуються, для запису 3D відео з послідовною розгорткою .
Зсув фаз
Дільники променя іноді використовують для рекомбінації променів світла, як у інтерферометрі Маха — Цендера. У цьому випадку є два вхідні промені та потенційно два вихідні. Але амплітуди двох вихідних променів — це суми (комплексних) амплітуд, розрахованих на основі кожного з вхідних променів, і це може призвести до того, що один із двох вихідних променів має амплітуду нуль. Для збереження енергії (див. Наступний розділ) повинен бути зсув фаз принаймні в одному із вихідних променів. Наприклад, якщо поляризована світлова хвиля в повітрі потрапляє на діелектричну поверхню, таку як скло, а електричне поле світлової хвилі знаходиться в площині поверхні, то відбита хвиля матиме фазовий зсув π, тоді як пропущена хвиля не матиме фазового зсуву. Так поведінка випливає з рівнянь Френеля.[2] Це не стосується часткового відбиття провідними (металевими) покриттями, де інші зсуви фаз відбуваються на всіх шляхах (відбиття та проходження). У будь-якому випадку деталі зсувів фаз залежать від типу та геометрії дільника променя.
Класичний дільник без втрат
Для класичних дільників променя без втрат з двома вхідними променями електричні поля, що падають на обидва його входи, два вихідних поля Ec і Ed лінійно пов'язані із входами через:
де елемент 2×2 є матрицею дільника променя, а r і t — це коефіцієнт відбиття та коефіцієнт пропускання вздовж певного шляху через дільник променя, причому цей шлях позначається індексами. (Значення залежать від поляризації світла.)
Якщо дільник променя не виводить енергію зі світлових променів, загальну вихідну енергію можна прирівняти до загальної вхідної енергії:
Ця вимога означає, що матриця дільника променя є унітарною.
Для збереження енергії повинні дотримуватись наступні залежності між відбивною здатністю та пропусканням
та
де «» означає комплексно спряжене.
Кожне r і t можна записати як комплексне число, що має амплітуду та фазовий коефіцієнт; наприклад, . Фазовий коефіцієнт враховує можливі зрушення у фазі променя, коли він відбивається або проходить через поверхню. Потім отримується
Після спрощення
що відповідає дійсності, коли і показник експоненти зменшується до -1. Після застосування цієї нової умови та піднесення у квадрат обох сторін отримано
де було зроблено заміну виду . Це призводить до результату
і так само,
Звідси випливає, що .
Визначивши обмеження, що описують дільник променя без втрат, початковий вираз можна переписати як
Використання в експериментах
Дільники променя використовувались як в уявних експериментах, так і в реальних експериментах в області квантової теорії та теорії відносності та інших галузях фізики. До них належать:
- Експеримент Фізо 1851 р. для вимірювання швидкості світла у воді
- Експеримент Майкельсона — Морлі 1887 р. для вимірювання впливу (гіпотетичного) світлового ефіру на швидкість світла
- Експеримент Гаммара 1935 р., щоб спростувати твердження Дейтона Міллера про позитивний результат повторень експерименту Майкельсона — Морлі
- Експеримент Кеннеді — Торндайка 1932 р. для перевірки незалежності швидкості світла та швидкості вимірювального приладу
- Експерименти з перевірки нерівності Белла (приблизно з 1972 р.) для демонстрації наслідків квантового заплутування та виключення теорії локальних прихованих змінних
- Експеримент із відкладеним вибором Уїлера 1978, 1984 та ін., щоб перевірити, що змушує фотон поводитися як хвиля або як частинка, і коли це відбувається
- Експеримент FELIX (запропонований у 2000 р.) для перевірки інтерпретації Пенроуза, що квантова суперпозиція залежить від кривини простору-часу
- Інтерферометр Маха — Цендера, що використовується в різних експериментах, включаючи тестер бомби Еліцура — Вейдмана, що включає вимірювання без взаємодії; та в інших в області квантових обчислень.
Квантовомеханічний опис
У квантовій механіці електричні поля є операторами, що пояснюється вторинним квантуванням. Кожен оператор електричного поля може бути далі виражений через моди, що представляють поведінку хвилі, та оператори амплітуди, які, як правило, представлені безрозмірними операторами народження та знищення. Отже, відношення амплітуд та перекладається у відношення операторів створення та
Суворе виведення наведене.[4]
Для діелектричного дільника променя з відношенням відбиття до пропускання 50:50 відбиті та передані промені відрізняються по фазі на = cos(pi/2) +/- i.sin(pi/2). Якщо припустити, що кожен переданий промінь зазнає зсуву фази , поля на вході та виході пов'язані між собою:
Унітарне перетворення, пов'язане з цим перетворенням, це
Використовуючи це унітарне перетворення, можна також записати перетворення як
Застосування для квантових обчислень
У 2000 р. Найл, Лафламме та Мілберн (протокол KLM) довели, що можна створити універсальний квантовий комп'ютер виключно з дільників променя, фазових перетворювачів, фотодетекторів та джерел одиничних фотонів[5]. Стани, які утворюють кубіт у цьому протоколі, є однофотонними станами двох мод, тобто станами | 01> і | 10> у поданні числа занять двох мод. Використовуючи ці ресурси, можна реалізувати будь-які одиничні кубітові вентилі та 2-кубітові імовірнісні вентилі. Дільник променя є важливим компонентом у цій схемі, оскільки він єдиний, який створює заплутаність між станами Фока.
Подібні налаштування існують для обробки квантової інформації з неперервними змінними. Насправді можна моделювати довільне перетворення Гаусса (Боголюбова) квантового стану світла за допомогою дільників променів, фазових перетворювачів та фотодетекторів, враховуючи стан двомодового стисненого вакуума доступний лише як попередній ресурс (отже, цей параметр має певну схожість із гауссовим аналогом протоколу KLM).[6] Основним елементом цієї процедури моделювання є той факт, що дільник променя еквівалентний перетворенню стиснення у частковій зворотності.
Див. також
- Направлений відгалужувач
- Дифракційний дільник променя
Примітки
- Beam Splitters. RP Photonics - Encyclopedia of Laser Physics and Technology. Процитовано 1 березня 2019.
- Zetie, K P; Adams, S F; Tocknell, R M. How does a Mach–Zehnder interferometer work?. Процитовано 13 лютого 2014.
- R. Loudon, The quantum theory of light, third edition, Oxford University Press, New York, NY, 2000.
- Fearn, H.; Loudon, R. (1987). Quantum theory of the lossless beam splitter. Optics Communications 64 (6): 485 – 490. doi:10.1016/0030-4018(87)90275-6.
- Knill, E.; Laflamme, R.; Milburn, G. J. (2001). A scheme for efficient quantum computation with linear optics. Nature (Nature Publishing Group) 409 (6816): 46–52. Bibcode:2001Natur.409...46K. PMID 11343107. doi:10.1038/35051009. Проігноровано невідомий параметр
|title-link=(довідка) - Chakhmakhchyan, Levon; Cerf, Nicolas (2018). Simulating arbitrary Gaussian circuits with linear optics. Physical Review A 98: 062314. arXiv:1803.11534. doi:10.1103/PhysRevA.98.062314.