Зірчастий багатогранник
Зірча́стий багатогра́нник (зірча́сте ті́ло) — неопуклий багатогранник, грані якого перетинаються між собою. Як і в незірчастих багатогранників, грані попарно з'єднуються в ребрах (при цьому внутрішні лінії перетину не вважають ребрами).
.stl.png.webp)
Термінологія
Зірчастою формою багатогранника називають багатогранник, отриманий продовженням граней даного багатогранника через ребра до їх наступного перетину з іншими гранями по нових ребрах.
Правильний зірчастий багатогранник — це зірчастий багатогранник, гранями якого є однакові (конгруентні) правильні або зірчасті багатокутники. На відміну від п'яти класичних правильних багатогранників (платонових тіл), ці багатогранники не є опуклими тілами.
1811 року Оґюстен Коші встановив, що існують всього 4 правильних зірчастих тіла (їх називають тілами Кеплера — Пуансо), які не є з'єднаннями платонових і зірчастих тіл. До них належать відкриті 1619 року Йоганном Кеплером малий зірчастий додекаедр і великий зірчастий додекаедр, а також великий додекаедр і великий ікосаедр, відкриті 1809 року Луї Пуансо. Інші правильні зірчасті багатогранники є або з'єднаннями платонових тіл, або з'єднаннями тіл Кеплера — Пуансо[1].
Напівправильні зірчасті багатогранники — це зірчасті багатогранники, грані яких є правильними або зірчастими багатокутниками, але не обов'язково однаковими. При цьому будова всіх вершин має бути однаковою (умова однорідності). Г. Коксетер, М. Лонге-Хіггінс і Дж. Міллер 1954 року перелічили 53 таких тіла і висунули гіпотезу про повноту свого списку[2]. Тільки значно пізніше в 1969 році Сопов С. П. довів, що їхній список багатогранників дійсно повний.
Багато форм зірчастих багатогранників зустрічаються в природі. Наприклад, сніжинки — це плоскі проєкції зірчастих багатогранників. Деякі молекули мають правильні структури об'ємних фігур.
На малюнках кожна грань для наочності пофарбована в інший колір.
 |
 |
 |
 |
Однорідні багатогранники — правильні і напівправильні опуклі багатогранники (платонові й архімедові тіла), правильні і напівправильні зірчасті багатогранники разом називають однорідними багатогранниками. У цих тіл всі грані є правильними багатокутниками (опуклими або зірчастими), а всі вершини однакові (тобто існують ортогональні перетворення багатогранника в себе, які переводять будь-яку вершину в будь-яку іншу). Існує 75 однорідних багатогранників.
Тетраедр і куб
Тетраедр і гексаедр (куб) не мають зірчастих форм, оскільки їх грані при продовженні через ребра більше не перетинаються.
Зірчастий октаедр
 |
Існує тільки одна зірчаста форма октаедра. Зірчастий октаедр відкрив Леонардо да Вінчі, потім через майже 100 років заново відкрив Й. Кеплер і назвав Stella octangula — восьмикутна зірка. Звідси ця форма має й другу назву: «stella octangula Кеплера»; по суті вона є з'єднанням двох тетраедрів.
 |
Зірчасті форми додекаедра
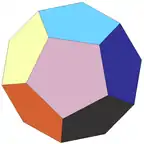 |
Додекаедр має 3 зірчасті форми: малий зірчастий додекаедр, великий додекаедр, великий зірчастий додекаедр (зірчастий великий додекаедр, завершальна форма). На відміну від октаедра, будь-яка з зірчастих форм додекаедра не є з'єднанням платонових тіл, а утворює новий багатогранник.
 |
 |
 |
У великого додекаедра гранями є п'яткутники, які сходяться по п'ять у кожній з вершин. У малого зірчастого і великого зірчастого додекаэдрів грані — п'ятикутні зірки (пентаграми), які в першому випадку сходяться по 5, а в другому по 3 грані в одній вершині.
Вершини великого зірчастого додекаедра збігаються з вершинами описаного додекаедра.
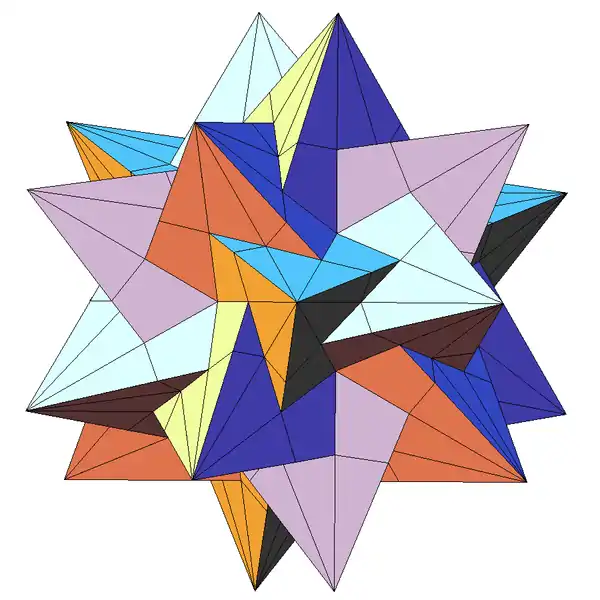
Зірчасті форми ікосаедра
 |
Ікосаедр має 59 зірчастих форм, з яких 32 мають повну, а 27 — неповну ікосаедральну симетрію, що довів Коксетер спільно з дю Валем, Флезером (H.T. Flather) і Петрі (John Flinders Petrie) із застосуванням правил обмеження, встановлених Дж. Міллером. Одна з цих зірчастих форм (20-а, модель 41 за Веннінґером), звана великим ікосаедром (див. рисунок), є одним з чотирьох правильних зірчастих багатогранників Кеплера — Пуансо. Його гранями є правильні трикутники, які сходяться в кожній вершині по п'ять; ця властивість великого ікосаедра спільна з ікосаедром.
Серед зірчастих форм також є: з'єднання п'яти октаедрів, з'єднання п'яти тетраедрів, з'єднання десяти тетраедрів. Перша зірчаста форма — малий триамбічний ікосаедр.
 |
 |
 |
Якщо кожну з граней продовжити необмежено, то тіло буде оточене великим розмаїттям відсіків — частин простору, обмежених площинами граней. Усі зірчасті форми ікосаедра можна отримати додаванням до початкового тіла таких відсіків. Не рахуючи самого ікосаедра, продовження його граней відокремлюють від простору 20 + 30 + 60 + 20 + 60 + 120 + 12 + 30 + 60 + 60 = 472 відсіки десяти різних форм і розмірів. Великий ікосаедр складається з усіх цих шматків, за винятком останніх шістдесяти. Наступна зірчаста форма — завершальна.
 |
Зірчасті форми кубооктаедра
 |
Кубооктаедр має 4 зірчасті форми, що задовольняють обмеженням, введеним Міллером. Перша з них є з'єднанням куба і октаедра.
 |
 |
 |
 |
Зірчасті форми ікосододекаедра
 |
Ікосододекаедр має багато зірчастих форм, перша з яких — з'єднання ікосаедра й додекаедра.
 |
 |
Икосододекаедр має 32 грані, з яких 12 є правильними п'ятикутниками, а решта 20 — правильними трикутниками.
Зведення до зірчастої форми
Під зведенням до зірчастої формі мають на увазі процес побудови багатогранника з іншого багатогранника шляхом розширення його граней. Для цього через грані початкового багатогранника проводять площини, розглядають різноманітні ребра, отримані внаслідок перетину цих площин, і вибирають відповідні.
Примітки
Література
- М. Веннинджер. Модели многогранников. — М. : Мир, 1974. — 236 с. (рос.)
- Гончар В. В. Модели многогранников. — М. : Аким, 1997. — 64 с. — ISBN 5-85399-032-2. (рос.)
- Гончар В. В. Модели многогранников. — Ростов-на-Дону : Феникс, 2010. — 143 с. — ISBN 978-5-222-17061-8. (рос.)
- Сoxeter H. S. M., Longuet-Higgins M. S., Miller J. C. P. Uniform Polyhedra // Phil. Trans. Roy. Soc. London. Ser. A, 246. — 1954. — P. 401—450. — DOI:10.1098/rsta.1954.0003.
- Сoxeter H. S. M. Regular Polytopes. 3rd ed. — New York : Dover, 1973. — 321 p. — ISBN 0-486-61480-8.
- Сопов С. П. Доказательство полноты перечня элементарных однородных многогранников // Украинский геометрический сборник. — 1970. — Т. 8 (8 листопада). — С. 139—156. (рос.)
Посилання
- Зірчасті форми додекаедра і переходи між ними в 3D (за допомогою миші і клавіші 1-4)
- Тривимірні моделі всіх однорідних багатогранників та їх зірчастих форм