Тіло Кеплера — Пуансо

Ті́ло Ке́плера — Пуансо́ — тіло, що являє собою правильний зірчастий багатогранник, який не є з'єднанням платонових і зірчастих тіл.

Великий додекаедр
Малий зірчастий додекаедр
Великий ікосаедр
Великий зірчастий додекаедр

1811 року французький математик Оґюстен Коші встановив, що існують всього 4 правильних зірчастих тіла, які не є з'єднаннями платонових і зірчастих тіл[1]. До них належать відкриті в 1619 році Йоганном Кеплером малий зірчастий додекаедр і великий зірчастий додекаедр, а також великий додекаедр і великий ікосаедр, відкриті 1809 року Луї Пуансо[2]. Інші правильні зірчасті багатогранники є або з'єднаннями платонових тіл, або з'єднаннями тіл Кеплера — Пуансо[3].

Історія
Мозаїка в соборі Святого Марка у Венеції, іноді приписувана Паоло Учелло.

Деякі з багатогранників Кеплера — Пуансо в тій чи іншій формі були відомі ще до Кеплера[4]. Так, зображення малого зірчастого додекаедра присутнє в мармуровій мозаїці, що прикрашає підлогу собору Святого Марка у Венеції. Ця мозаїка датується XV століттям, авторство іноді приписують Паоло Учелло. В XVI столітті німецький ювелір Венцель Ямнітцер у своїй праці Perspectiva corporum regularium (Перспективи правильних тіл) зображує великий додекаедр і великий зірчастий додекаедр[5]. Напевно, до Кеплера ніхто з художників і вчених не знав усіх властивостей цих тіл.

Малий і великий зірчасті додекаэдри, які іноді називають «багатогранники Кеплера», вперше повністю описано в трактаті Йоганна Кеплера 1619 року Harmonices Mundi[6]. Кожне з цих тіл має центральну опуклу ділянку кожної грані, «приховану» всередині, при цьому видно тільки трикутні площини. Кеплер описує багатогранники, використовуючи ту ж модель, за допомогою якої Платон у діалозі Тімей описує побудову правильних багатогранників на основі правильних трикутників[7]. Останнім кроком Кеплера було визнання, що ці багатогранники є правильними, навіть якщо вони не є опуклими, на відміну від звичайних платонових тіл.

1809 року Луї Пуансо знову дослідив багатогранники Кеплера і виявив ще два правильних зірчастих багатогранники — великий ікосаедр і великий додекаедр[2]. При цьому Пуансо не був упевнений, що виявив всі можливі види правильних зірчастих багатогранників. Але 1811 року Оґюстен-Луї Коші довів, що існують всього 4 правильних зірчастих тіла, які не є з'єднаннями платонових і зірчастих тіл, а 1858 року Жозеф Бертран надав більш загальне доведення[4]. У 1859 році Артур Келі дав багатогранникам Кеплера — Пуансо назви, під якими вони, як правило, відомі сьогодні. Сто років потому Джон Конвей розробив термінологію для зірчастих багатокутників. У рамках цієї термінології він запропонував дещо змінені назви двох правильних зірчастих багатогранників[8].

Термінологія Келі Термінологія Конвея
Малий зірчастий додекаедр Зірчастий додекаедр
Великий додекаедр Великий додекаедр
Великий зірчастий додекаедр Зірчастий великий додекаедр
Великий ікосаедр Великий ікосаедр

Термінологія Конвея нині використовується, але не має широкого розповсюдження.

Характеристики

Неопуклість

Ці тіла мають грані і вершинні фігури у вигляді п'ятикутників. Малий і великий зірчастий додекаедри мають грані у вигляді неопуклих правильних зірок. Великий додекаедр і великий ікосаедр мають опуклі грані[9][10].

У всіх цих тіл дві грані можуть перетинатися, утворюючи лінію, яка не є ребром якоїсь із них, таким чином, частина кожної грані проходить через внутрішню частину тіла. Такі лінії перетину іноді називають хибними ребрами. Аналогічно, коли три такі лінії перетинаються в точці, яка не належить куту якоїсь грані, ці точки називають хибними вершинами. Наприклад, малий зірчастий додекаедр має 12 п'ятикутних граней з центральною п'ятикутною частиною, прихованою всередині тіла. Видимі частини кожної грані складаються з п'яти рівнобедрених трикутників, які дотикаються в п'яти точках. Можна розглянути ці трикутники як 60 окремих граней, що утворюють новий, неправильний багатогранник, який зовні виглядає ідентичним первинному. Кожне ребро тепер ділиться на три коротких ребра (двох різних видів), при цьому 20 хибних вершин стануть істинними, і, таким чином, загалом тіло матиме 32 вершини (знову ж таки двох видів). Приховані внутрішні п'ятикутники більше не будуть частинами багатогранної поверхні, і можуть зникнути. Тепер Ейлерова характеристика містить: 60 — 90 + 32 = 2. Але цей новий багатогранник вже не описується символом Шлефлі {5/2, 5}, і тому не є тілом Кеплера — Пуансо, хоча виглядає, як одне з них[10].

Характеристика Ейлера χ

Тіла Кеплера — Пуансо покривають площу описаних навколо них сфер більше одного разу, при цьому центри граней виступають точками перегину на поверхнях, які мають п'ятикутні грані, і вершинами — на інших поверхнях. Тому тіла Кеплера — Пуансо не обов'язково топологічно еквівалентні сфері, на відміну від платонових тіл, і, зокрема, характеристика Ейлера

для них не завжди має місце. Шлефлі встановив, що всі багатогранники повинні мати χ = 2, і вважав, що малий зірчастий додекаедр і великий додекаедр не є правильними багатогранниками[11]. Ця точка зору не була поширеною.

Модифікована форма формули Ейлера, виведена Артуром Келі[4], справедлива як для опуклих багатогранників, так і для тіл Кеплера — Пуансо, виглядає так:

.

Двоїстість

Тіла Кеплера — Пуансо існують у двоїстих (дуальних) парах[12]:

Зведена таблиця властивостей

Властивості тіл Кеплера-Пуансо наведено в наступній таблиці[13]:

Назва Зображення Сферична проекція Діаграма
зірчастого багатогранника		 Символ Шлефлі
{p, q}		 Грані
{p}		 Ребра Вершини χ Щільність Групи симетрії Двоїстий багатогранник
Малий зірчастий додекаедр



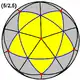 {5/2,5} 12
{5/2}
 30 12
{5}
 -6 3 Ih Великий додекаедр
Великий додекаедр



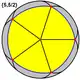 {5,5/2} 12
{5}
 30 12
{5/2}
 -6 3 Ih Малий зірчастий додекаедр
Великий зірчастий додекаедр



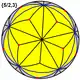 {5/2,3} 12
{5/2}
 30 20
{3}
 2 7 Ih Великий ікосаедр
Великий ікосаедр



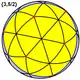 {3,5/2} 20
{3}
 30 12
{5/2}
 2 7 Ih Великий зірчастий додекаедр

Відношення між правильними багатогранниками
Мають однакове розташування вершин: Мають одні і ті ж
вершини і ребра:

Ікосаедр, малий зірчастий додекаедр, великий ікосаедр і великий додекаедр.
Малий зірчастий додекаедр і великий ікосаедр.

Додекаедр і великий зірчастий додекаедр.
Ікосаедр і великий додекаедр.

Малий зірчастий додекаедр і великий ікосаедр мають одні і ті ж вершини і ребра. Ікосаедр і великий додекаедр також мають одні і ті ж вершини і ребра.

Всі три додекаедри є зірчастими правильними опуклими додекаедрами, великий ікосаедр є зірчастим правильним опуклим ікосаедром[14].

Якщо при перетині виникають нові ребра і вершини, отримані багатогранники не будуть правильними, але їх ще можна вважати зірчастими.

У масовій культурі й мистецтві
Зірка Александера

У XX столітті відомий представник імп-арту Мауріц Ешер у своїй творчості нерідко звертався до сюжетів, заснованих на сприйнятті різних багатовимірних фігур; зокрема, його літографія Гравітація зображує малий зірчастий додекаедр[15].

В основу перестановкової головоломки 1980-х років — зірки Александера — покладено великий додекаедр[16].

Див. також

Примітки
  1. Cauchy, 1813, с. 68-86.
  2. Poinsot, 1810, с. 16-48.
  3. Wenninger, 1983, с. 46.
  4. Stellation and facetting — a brief history
  5. Jamnitzer-Galerie a
  6. Harmonices mundi
  7. Field, 1984, с. 207-219.
  8. Conway, Burgiel, Goodman-Strauss, 2008, с. 404-408.
  9. Great Dodecahedron
  10. Small Stellated Dodecahedron
  11. Schläfli, 1901.
  12. Dual Polyhedron
  13. Kepler-Poinsot Solid
  14. Great Icosahedron
  15. Эшер, 2009.
  16. Alexander's Star

Література
  • М. Веннинджер . Модели многогранников. — М. : Мир, 1974. — 236 с.
  • Эшер М.К. Графика. — М. : Арт-Родник, Taschen, 2009. — 96 с. — ISBN 978-5-404-00053-5.
  • J. Bertrand. Note sur la théorie des polyèdres réguliers. — 1858. — Т. 46. — P. 79-82, 117.
  • Augustin Louis Cauchy. Recherches sur les polyèdres. — J. de l'École Polytechnique 9. — 1813. — P. 68-86.
  • Arthur Cayley. On Poinsot’s Four New Regular Solids. — Philos. Mag. — 1859. — Т. 17. — P. 123—127 и 209.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 24, Regular Star-polytopes // The Symmetry of Things. — 2008. — P. 404—408. — ISBN 978-1-56881-220-5.
  • H.S.M. Coxeter. (Paper 1), The Nine Regular Solids [Proc. Can. Math. Congress 1 (1947), 252—264, MR 8, 482] // Kaleidoscopes: Selected Writings of H.S.M. Coxeter / edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
  • H.S.M. Coxeter. (Paper 10), Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25-36] // Kaleidoscopes: Selected Writings of H.S.M. Coxeter / edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
  • P. Cromwell. Polyhedra. — Cabridgre University Press, Hbk, 1997.
  • Field, J. V. A Lutheran astrologer: Johannes Kepler. — Archive for History of Exact Sciences. — 1984. — Т. 31, No. 3. — P. 207—219.
  • Theoni Pappas. (The Kepler-Poinsot Solids) The Joy of Mathematics. — San Carlos, CA : Wide World Publ./Tetra, 1989. — P. 113.
  • Louis Poinsot. Memoire sur les polygones et polyèdres. — J. de l'École Polytechnique. — 1810. — Т. 9. — P. 16-48.
  • Lakatos, Imre. Proofs and Refutations. — Cambridge University Press, 1976.
  • Schläfli, Ludwig. Theorie der vielfachen Kontinuität / editor J. H.Graf. — Republished by Cornell University Library historical math monographs 2010. — Zürich, Basel : Georg & Co, 1901. — ISBN 978-1-4297-0481-6.
  • Wenninger, Magnus. Dual Models. — Cambridge University Press, 1983. — P. 39-41. — ISBN 0-521-54325-8.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.