Наближення порожньої ґратки
Наближення порожньої ґратки — це модель зонної теорії кристалів, в якій потенціал кристалічної ґратки періодичний та ґранично слабкий. Енергія електронів у «порожній ґратці» точно така сама, як і вільних електронів. Головним здобутком такого підходу є схема класифікації електронних зон[1]:245, а практично застосовними є лише його розширення, зокрема, у вигляді ґраничних випадків майже вільних електронів та сильного зв'язку.
Розсіювання та періодичність
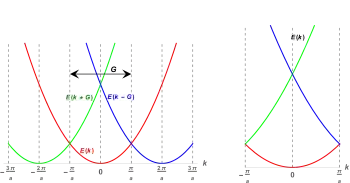
Розсіювання електронів на вузлах ґратки визначається просторовим розташуванням вузлів. Кожен вузол є потенціальною ямою, на якій з певною ймовірністю відбудеться акт розсіювання. Для частинки в одновимірній ґратці, зокрема, модель Кроніга-Пенні дає можливість аналітично обчислити зонну структуру за відомими значеннями потенціалу, відстані між сусідніми атомами та розміру потенціальної ями. Для дво- і тривимірних випадків подібні моделі з невеликою кількістю параметрів дають нереалістичні розв'язки.[2]:310 Тим не менше, в більшості областей зонну структуру вдається наближено описати за допомогою теорії збурень, починаючи з розв'язків для порожньої ґратки, тобто плоских хвиль.[1]:245
В наближенні порожньої ґратки електрони мають лише кінетичну енергію й закон дисперсії виглядає так:
- .
Тут — зведена стала Планка, m — маса електрона, — вектор оберненого простору, який називають квазіімпульсом.
Якою малою не була би глибина потенціальної ями, у нескінченній періодичній ґратці рано чи пізно акт взаємодії відбудеться й хвилю буде відбито. Такий процес розсіювання зумовлює відомий закон Брегга, а також періодичність закону дисперсії електронів і поділ -простору на зони Бріллюена. Періодичність закону дисперсії математично виражається так.[1]:245 Якщо два -вектори різняться на будь-який вектор оберненої гратки, , то їм відповідає одне й те саме значення енергії, .
Завдяки цій періодичності для маркування всіх точок достатньо обмежитися такими значеннями , які лежать всередині першої зони Бріллюена; в поданому прикладі одновимірної лінійної ґратки зі сталою ґратки це значення . В такий спосіб у схемі зведених зон з'являються різні гілки закону дисперсії, їх доводиться додатково нумерувати: .
Енергетичні зони й густина станів
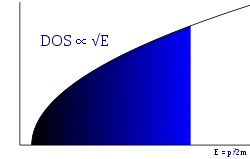
Густина станів (англ. DOS) — це кількість електронних станів в інтервалі енергій , пронумерованому векторами оберненого простору. В одновимірному випадку густина станів, створювана зоною при даній енергії , тим більша, чим менше значення похідної .
Хоча елементарні комірки не є сферично симетричними, в наближеннях порожньої ґратки та майже вільних електронів квадратичний вигляд закону дисперсії зберігається. Порівняно з одновимірним, у дво- й тривимірному випадках кількість станів, що потрапляють в інтервал , збільшується внаслідок можливого виродження по напрямку вектора . Для тривимірної ґратки густина станів пропорційна кореню квадратному з енергії, який при квадратичному законі дисперсії у свою чергу пропорційний квазіімпульсу:
- .
Друга й вищі зони Бріллюена
Вільні електрони, що рухаються порожньою ґраткою із хвильовим вектором поза першою зоною Бріллюена, будуть відбиті до першої зони Бріллюена. Хоча дуже схожий на вектор імпульсу, зберігається лише квазіімпульс, тобто зберігається з точністю до , будь-якого вектору зворотної ґратки. В зовнішніх посиланнях можна знайти онлайн-ресурси із прикладами та зображеннями вищих зон Бріллюена.
Модель майже вільних електронів
В багатьох звичайних металах, на кшталт алюмінію, ефект екранування значно послаблює електростатичне поле, створюване іонами ґратки при металічному зв'язку. Електростатичний потенціал в кристалі виражається як
- ,
де Z — атомний номер металу, e — елементарний заряд, r — відстань між електроном і ядром іону, q — параметр екранування, що обмежує дальнодію потенціалу. Перетворення Фур'є, , потенціалу ґратки дається формулою
- .
Значення недіагональних елементів потенціалу (між різними векторами зворотної ґратки) майже дорівнюють нулю. В результаті величина забороненої зони спадає й результат стає подібним до передбаченого в наближенні порожньої ґратки.
Електронні зони поширених ґраток металів
За винятком кількох екзотичних структур, переважна більшість металів кристалізується в одному з трьох структурних типів: об'ємноцентрована чи гранецентрована кубічна структура, або щільноупакована гексагональна структура.
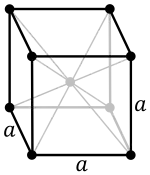 Об'ємноцентрована кубічна (ОЦК, символ I)
Об'ємноцентрована кубічна (ОЦК, символ I) Гранецентрована кубічна (ГЦК, символ F)
Гранецентрована кубічна (ГЦК, символ F)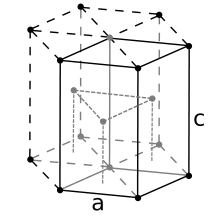
.png.webp) Перша зона Бріллюена ОЦК ґратки
Перша зона Бріллюена ОЦК ґратки Перша зона Бріллюена ГЦК ґратки
Перша зона Бріллюена ГЦК ґратки Перша зона Бріллюена ГЩ ґратки
Перша зона Бріллюена ГЩ ґратки


Джерела
- Киттель Ч. (1967). Квантовая теория твёрдых тел (російською). М.: Наука.
- Киттель Ч. (1978). Введение в физику твёрдого тела (російською). М.: Наука.