Напівлокально однозв'язний простір

Топологічний простір X називається напівлокально однозв'язним, якщо для кожної точки простору X існує окіл U з властивістю, що кожна петля у U може бути стягнута в одну точку в X, тобто її клас гомотопії у просторі X є тривіальним. Окіл U не обов'язково має бути однозв'язним: хоча кожна петля в U має бути гомотопною одиниці в просторі X, вона може не бути гомотопною одиниці в U.

Еквівалентно X є напівлокально однозв'язним простором якщо кожна точка в X має окіл U, для якого гомоморфізм з фундаментальної групи U у фундаментальну групу X, індукований включенням множини U в X, є тривіальним гомоморфізмом (тобто його образ є одиничним елементом).

Більшість основних теорем теорії накриттів, зокрема існування універсального накриття вимагає щоб базовий простір був лінійно зв'язаним, локально лінійно зв'язаним і напівлокально однозв'язним. Умова напівлокальної однозв'язності є необхідною для існування однозв'язного накриття, а при інших вказаних умовах і достатньою.

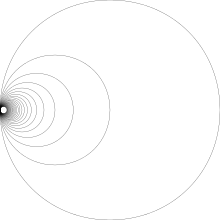
Типовим прикладом простору, що не є напівлокально однозв'язним є гавайська сережка: об'єднання на площині кіл виду ${\displaystyle C_{n}=\left\{(x,y)\in \mathbb {R} ^{2}{\Big |}\left(x-{\frac {1}{n}}\right)^{2}+y^{2}={\frac {1}{n^{2}}}\right\}}$із індукованою топологією. Тоді кожен окіл початку координат містить нескінченну кількість кіл, які не є гомотопними точці.

Іншим прикладом простору, що не є напівлокально однозв'язним є доповнення множини Q × Q на площині R², де Q — множина раціональних чисел. Фундаментальна група цього простору є незліченною.

• Локально однозв'язний простір
• Універсальне накриття

• Bourbaki, Nicolas (2016). Topologie algébrique: Chapitres 1 à 4. Springer. Ch. IV pp. 339 -480. ISBN 978-3662493601.
• J.S. Calcut, J.D. McCarthy Discreteness and homogeneity of the topological fundamental group Topology Proceedings, Vol. 34,(2009), pp. 339–349
• Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.