Накриття (топологія)
Накриття — неперервне сюр'єктивне відображення топологічного простору X на топологічний простір Y, таке, що для будь-якої точки знайдеться окіл , повний прообраз якого є об'єднанням відкритих множин , що не перетинаються:
- ,
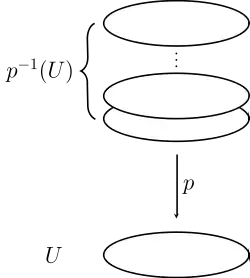
причому на кожній множині відображення є гомеоморфізмом між і .
Пов'язані визначення
- Простір Y називається базою накриття, а X — простором накриття (або накриваючим простором).
- Прообраз точки називають шаром над точкою .
- Число областей Vk в повному прообразі називається числом листів.
- Якщо це число скінченне і рівне n, то накриття називається n-листовим.
- Накриття називається універсальним якщо накриваючий простір є однозв'язним.
Приклади
- Нехай позначає одиничне коло комплексної площини .
- .
- , де , .
- Нехай — тор. Тоді є накриваючим простором і накриття задається формулою:
- .
Властивості
- Нехай — накриття і — відкрита підмножина простору X. Тоді множина p(U) е відкритою у Y.
- Нехай — накриття і Z — зв'язний і локально-зв'язний простір. Нехай — неперервні відображення, що задовольняють умови
- для деякого
- тоді
- Накриття є частковими випадками локально тривіальних розшарувань. Їх можна розглядати як локально тривіальні розшарування з дискретним шаром.
Зв'язок з фундаментальною групою
Зазвичай накриття розглядається в припущенні зв'язності і а також локальної зв'язності і локальної однозв'язності . При цих припущеннях встановлюється зв'язок між фундаментальними групами і : якщо , то індукований гомоморфізм , відображає ізоморфно на підгрупу в і, міняючи точку у , можна одержати в точності всі підгрупи з деякого класу спряжених підгруп.
Якщо цей клас складається з однієї підгрупи (тобто — нормальна підгрупа), те накриття називається регулярним. В цьому випадку виникає вільна дія групи на , причому виявляється фактор-відображенням на простір орбіт .
Взагалі, вільні дії дискретних груп — типове джерело регулярних накриттів (над простором орбіт, хоч і не всяка така дія задає накриття, простір орбіт може виявитися невіддільним).
Ця дія породжується підняттям петель: якщо петлі , , зіставити єдиний шлях , для якого і , то точка залежатиме тільки від класу цієї петлі в і від точки . Таким чином, елементу з відповідає перестановка точок в . Ця перестановка не має нерухомих точок, і неперервно залежить від точки . Це визначає гомеоморфізм , що комутує з .
У загальному випадку ця конструкція визначає лише перестановку в , тобто дію на , що називається монодромією накриття.
Окремим випадком регулярного накриття є універсальне накриття, для якого або, що еквівалентно, X — однозв'язний простір.
Взагалі, по кожній групі однозначно будується накриття , для якого образ є .
Для будь-якого відображення лінійно зв'язного простору у підняття його до відображення існує тоді і тільки тоді, коли образ лежить в . Між накриттями є відношення часткового порядку (накриття деякого накриття простору X теж є накриттям простору X), подвійне включенню підгруп в . Зокрема, універсальне накриття є єдиним максимальним елементом.
Див. також
Література
- Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия. Методы и приложения. — М. : Наука, 1986. — 760 с.
- Хатчер А. Алгебраическая топология. — М. : МЦНМО, 2011. — 688 с.
- Massey W. A Basic Course in Algebraic Topology. — Springer, 1991. — ISBN 0-387-97430-X.
- Singer I., Thorpe J. A. Lecture Notes on Elementary Geometry and Topology. — Springer, 1967. — ISBN 0-387-90202-3.
