Об'єднання множин

Об'єднання множин A та B

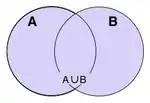
Якщо A та B — множини, то об'єднанням A та B є множина, яка включає всі елементи A і всі елементи B, і більш нічого.

Об'єднання множин A та B позначається як «A∪B».

Формально:

x є елементом A∪B тоді й тільки тоді, коли

• x є елементом A або
• x є елементом B.

Наприклад, об'єднанням множин {1, 2, 3} та {2, 3, 4} буде {1, 2, 3, 4}.

Бінарна операція об'єднання є :

• асоціативною, тобто A∪(B∪C) = (A∪B)∪C   (отже, коли в виразі є тільки операція об'єднання, дужки можна не писати: A∪B∪C);

• комутативною, тобто A∪B = B∪A   (отже, порядок запису множин в виразі не має значення).

Порожня множина є нейтральним елементом для операції об'єднання в алгебрі множин. Тобто, Ø∪A = A, для будь-якої множини A.

• ідемподентною, тобто A∪A = A.

В загальному випадку, якщо M — множина, елементами якої є також множини, то x є елементом M тоді й тільки тоді, якщо існує такий елемент A з M, що x є елементом A. В символічній формі:

${\displaystyle x\in \bigcup \mathbf {M} \iff \exists A{\in }\mathbf {M} ,x\in A.}$

Позначення об'єднання довільної кількості множин такі:

${\displaystyle \bigcup \mathbf {M} ,}$ або ${\displaystyle \bigcup _{A\in \mathbf {M} }A.}$

Остання нотація може бути узагальнена до

${\displaystyle \bigcup _{i\in I}A_{i},}$

що відповідає операції об'єднання колекції множин {A_i : i в I}. Тут I — множина, а A_i — множина для кожного i в I.

В цьому випадку I є множиною індексів (натуральних чисел), і нотація є аналогічною узагальненій операції сумування:

${\displaystyle \bigcup _{i=1}^{\infty }A_{i}.}$

Також можна записати «A₁ ∪ A₂ ∪ A₃ ∪ ···».

Перетин множин є дистрибутивним відносно об'єднання, тобто

${\displaystyle \bigcup _{i\in I}(A\cap B_{i})=A\cap \bigcup _{i\in I}B_{i}.}$

Можна об'єднати таке нескінченне об'єднання з нескінченним перетином, отримавши співвідношення:

${\displaystyle \bigcup _{i\in I}(\bigcap _{j\in J}A_{i,j})\subseteq \bigcap _{j\in J}(\bigcup _{i\in I}A_{i,j}).}$

• Диз'юнкція

• Куратовский К., Мостовский А. Теория множеств. — Москва : Мир, 1970. — 416 с.(рос.)