Біпіраміда
Біпіраміда або дипіраміда є тривимірним багатогранником, сформованим з двох пірамід, одна з яких є дзеркальним відображенням іншої[1]. Місце з'єднання пірамід утворює спільну фігуру у вигляді багатокутника. Найпростіша біпіраміда формується при складанні двох тетраедрів. За основи піраміди у вигляді квадрата, причому, якщо бічні грані її — рівносторонні трикутники, формується біпіраміда, відома як октаедр. Шестикутна біпіраміда утворюється з пірамід, в основі яких лежить правильний шестикутник. При збільшенні числа сторін багатокутника в основі піраміди, в границі формується круг або еліпс і утворюється два конуси, з'єднані основами.
| Геометрія |
|---|
 |
| Історія |
|
|
|
|
|
Елементи, що складають біпіраміду:
- Ребра — відрізки, що з'єднують вершини.
- Грані — плоскі поверхні, обмежені ребрами, трикутної або трапецієвидної форми.
| Багатогранник | 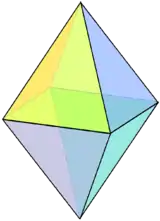 |
 |
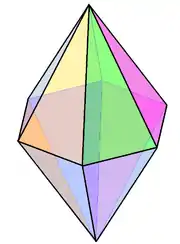 |
 |
 |
 | |||
|---|---|---|---|---|---|---|---|---|---|
| Коксетер | |||||||||
| Мозаїка |  |
 |
 |
 |
 |
 |
 | ||
| Конфігурація | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
Біпіраміди складної геометрії
Біпіраміда як термін може застосовуватися і для характеристики об'єктів, які складаються з двох пірамід незалежно від симетрії, дзеркальності частин або форми з'єднання частин. Елементарні форми біпірамід застосовують для опису більш складних форм кристалів, наприклад, при ограновуванні кристалів (алмазів). Наприклад, форму октаедра, що складається з двох зрізаних пірамід (тетрагональна зрізана біпіраміда) або кардіоїд (форма обробленого алмазу), одна частина якого має форму піраміди, а друга частина — форму зрізаної піраміди.
З'єднання двох тетраедрів може дати і складнішу форму у вигляді тригональної зірчастої біпіраміди. Реальні форми кристалів значно відрізняються від наведених вище ідеальних форм, які розглядає геометрія.
У формі октаедра кристалізуються: алмази, хлорид натрію, перовськіт, олівін, флюорит, шпінель.
Примітки
- Бипирамиды // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп. т.). — СПб., 1890—1907. (рос. дореф.)
Посилання
- http://www.cnshb.ru/AKDiL/0042/base/RD/000485.shtm
- https://web.archive.org/web/20090207143009/http://www2.polito.it/didattica/polymath/htmlS/argoment/Matematicae/Giugno_06/TetraUnit/