Передавальна функція штучного нейрона
Функція активації, або передавальна функція (англ. activation function[1][2][3][4][5], також excitation function, squashing function, transfer function[6]) штучного нейрона — залежність вихідного сигналу штучного нейрона від вхідного.
Зазвичай передавальна функція відображає дійсні числа на інтервал або [1].
Більшість видів нейронних мереж для функції активації використовують сигмоїди[2]. ADALINE і самоорганізаційні карти використовують лінійні функції активації, а радіально базисні мережі використовують радіальні базисні функції[1].
Математично доведено, що тришаровий перцептрон з використанням сигмоїдної функції активації може апроксимувати будь-яку неперервну функцію з довільною точністю (Теорема Цибенка)[1].
Метод зворотного поширення помилки вимагає, щоб функція активації була неперервною, нелінійною, монотонно зростаючою, і диференційовною[1].
В задачі багатокласової класифікації нейрони останнього шару зазвичай використовують softmax як функцію активації[3].
У хемометриці — функція, яка використовується в методі нейронної сітки для перетворення у вузлах вхідних даних з будь-якої області значень (зокрема неперервних) у чітко окреслений ряд значень (напр., в 0 чи 1).[7]
Порівняння передавальних функцій
Деякі бажані властивості передавальної функції включають:
- Нелінійна — коли передавальна функція нелінійна, то, як доведено, двошарова нейронна мережа є універсальною апроксимацією функцій.[8] Тотожна передавальна функція не має такої властивості. Коли декілька шарів використовують тотожну передавальну функцію, тоді вся мережа еквівалентна одношаровій моделі.
- Неперервна диференційовність — ця властивість бажана (RELU не є неперервно диференційовною і має неоднозначне рішення для оптимізації заснованій на градієнті) для використання методів оптимізації заснованих на градієнті. Передавальна функція двійковий крок не диференційовна у 0, але диференційовна в усіх інших значення, що є проблемою для методів заснованих на градієнті.[9]
- Область визначення.
- Монотонність.
- Гладка функція з монотонною похідною.
- Наближення до тотожної функції в початку координат.
У наступній таблиці порівнюються деякі передавальні функції від однієї змінної x з попереднього шару:
| Назва | Графік | Рівняння | Похідна (по x) | Область | Порядок гладкості | Монотонність | Монотонність похідної | Наближення до Тотожної функції в початку координат |
|---|---|---|---|---|---|---|---|---|
| Тотожна | 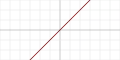 |
Так | Так | Так | ||||
| Двійковий крок |  |
Так | Ні | Ні | ||||
| Логістична (a.k.a. Сігмоїда або М'який крок) |  |
Так | Ні | Ні | ||||
| TanH | 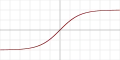 |
Так | Ні | Так | ||||
| ArcTan |  |
Так | Ні | Так | ||||
| Softsign[10][11] |  |
Так | Ні | Так | ||||
| Inverse square root unit (ISRU)[12] | Так | Ні | Так | |||||
| Випрямлена лінійна (Rectified linear unit, ReLU)[13] |  |
Так | Так | Ні | ||||
| Leaky rectified linear unit (Leaky ReLU)[14] |  |
Так | Так | Ні | ||||
| Parameteric rectified linear unit (PReLU)[15] |  |
Так ↔ | Так | Так ↔ | ||||
| Randomized leaky rectified linear unit (RReLU)[16] |  |
Так | Так | Ні | ||||
| Exponential linear unit (ELU)[17] |  |
Так ↔ | Так ↔ | Так ↔ | ||||
| Scaled exponential linear unit (SELU)[18] |
з та |
Так | Ні | Ні | ||||
| S-shaped rectified linear activation unit (SReLU)[19] | are parameters. |
Ні | Ні | Ні | ||||
| Inverse square root linear unit (ISRLU)[12] | Так | Так | Так | |||||
| Adaptive piecewise linear (APL)[20] | Ні | Ні | Ні | |||||
| SoftPlus[21] | 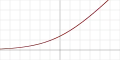 |
Так | Так | Ні | ||||
| Bent identity | 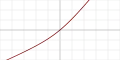 |
Так | Так | Так | ||||
| Sigmoid-weighted linear unit (SiLU)[22] (a.k.a. Swish[23]) | Ні | Ні | Ні | |||||
| SoftExponential[24] |  |
Так | Так | Так ↔ | ||||
| Синусоїда[25] |  |
Ні | Ні | Так | ||||
| Sinc |  |
Ні | Ні | Ні | ||||
| Гауссіан |  |
Ні | Ні | Ні |
- ↑ Тут, H це функція Гевісайда.
- ↑ α є стохастичною змінною вибраною з нормального розподілу під час навчання і зафіксована як очікуване значення розподілу до часу тестування.
- ↑ ↑ ↑ Тут, — логістична функція.
- ↑ виконується для всього інтервалу.
Наступна таблиця містить передавальні функції від декількох змінних:
| Назва | Рівняння | Похідна(ні) | Область | Порядок гладкості |
|---|---|---|---|---|
| Softmax | for i = 1, …, J | |||
| Maxout[26] |
↑ Тут, — символ Кронекера.
Див. також
Примітки
- Ke-Lin Du, Swamy M. N. S., Neural Networks and Statistical Learning, Springer-Verlag London, 2014 DOI:10.1007/978-1-4471-5571-3
- James Keller, Derong Liu, and David Fogel: Fundamentals of computational intelligence: neural networks, fuzzy systems, and evolutionary computation: John Wiley and Sons, 2016, 378 pp, ISBN 978-1-110-21434-2
- Lionel Tarassenko, 2 - Mathematical background for neural computing, In Guide to Neural Computing Applications, Butterworth-Heinemann, New York, 1998, Pages 5-35, ISBN 9780340705896, http://doi.org/10.1016/B978-034070589-6/50002-6.
- Anthony, Martin (2001). 1. Artificial Neural Networks. с. 1–8. doi:10.1137/1.9780898718539.
- Michael Nielsen. Neural Networks and Deep Learning.
- Stegemann, J. A.; N. R. Buenfeld (2014). A Glossary of Basic Neural Network Terminology for Regression Problems. Neural Computing & Applications 8 (4): 290–296. ISSN 0941-0643. doi:10.1007/s005210050034.
- Глосарій термінів з хімії // Й. Опейда, О. Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л. М. Литвиненка НАН України, Донецький національний університет. — Донецьк: Вебер, 2008. — 758 с. — ISBN 978-966-335-206-0
- Cybenko, G.V. (2006). Approximation by Superpositions of a Sigmoidal function. У van Schuppen, Jan H. Mathematics of Control, Signals, and Systems. Springer International. с. 303–314.
- Snyman, Jan (3 березня 2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.
- Bergstra, James; Desjardins, Guillaume; Lamblin, Pascal; Bengio, Yoshua (2009). Quadratic polynomials learn better image features". Technical Report 1337. Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Архів оригіналу за 25 вересня 2018.
- Glorot, Xavier; Bengio, Yoshua (2010). Understanding the difficulty of training deep feedforward neural networks. International Conference on Artificial Intelligence and Statistics (AISTATS’10). Society for Artificial Intelligence and Statistics.
- Carlile, Brad; Delamarter, Guy; Kinney, Paul; Marti, Akiko; Whitney, Brian (2017-11-09). «Improving Deep Learning by Inverse Square Root Linear Units (ISRLUs)». arXiv:1710.09967 [cs.LG].
- Nair, Vinod; Hinton, Geoffrey E. (2010). Rectified Linear Units Improve Restricted Boltzmann Machines. 27th International Conference on International Conference on Machine Learning. ICML'10. USA: Omnipress. с. 807–814. ISBN 9781605589077.
- Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (June 2013). Rectifier nonlinearities improve neural network acoustic models. Proc. ICML 30 (1). Архів оригіналу за 3 січня 2017. Процитовано 2 січня 2017.
- He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015-02-06). «Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification». arXiv:1502.01852 [cs.CV].
- Xu, Bing; Wang, Naiyan; Chen, Tianqi; Li, Mu (2015-05-04). «Empirical Evaluation of Rectified Activations in Convolutional Network». arXiv:1505.00853 [cs.LG].
- Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015-11-23). «Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)». arXiv:1511.07289 [cs.LG].
- Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (2017-06-08). «Self-Normalizing Neural Networks». arXiv:1706.02515 [cs.LG].
- Jin, Xiaojie; Xu, Chunyan; Feng, Jiashi; Wei, Yunchao; Xiong, Junjun; Yan, Shuicheng (2015-12-22). «Deep Learning with S-shaped Rectified Linear Activation Units». arXiv:1512.07030 [cs.CV].
- Forest Agostinelli; Matthew Hoffman; Peter Sadowski; Pierre Baldi (21 грудня 2014). «Learning Activation Functions to Improve Deep Neural Networks». arXiv:1412.6830 [cs.NE].
- Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). Deep sparse rectifier neural networks. International Conference on Artificial Intelligence and Statistics.
- Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning
- Searching for Activation Functions
- Godfrey, Luke B.; Gashler, Michael S. (3 лютого 2016). A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks. 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management: KDIR 1602: 481–486. Bibcode:2016arXiv160201321G. arXiv:1602.01321.
- Gashler, Michael S.; Ashmore, Stephen C. (2014-05-09). «Training Deep Fourier Neural Networks To Fit Time-Series Data». arXiv:1405.2262 [cs.NE].
- Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (18 лютого 2013). Maxout Networks. JMLR WCP 28 (3): 1319–1327. Bibcode:2013arXiv1302.4389G. arXiv:1302.4389.