Перетворення Келі

Перетворення Келі — схожі результати в теорії матриць, комплексному аналізі та для самоспряжених операторів. Названі на честь англійського математика Артура Келі.

Матриці

Перетворення Келі для квадратних матриць:

\ A^{C}=(I-A)(I+A)^{-1}

перетворення Келі є інволюцією A = (A^c)^c
для дійсних матриць перетворює кососиметричну матрицю S (таку що, S^T = −S) в ортогональну матрицю Q (таку що, Q^TQ = I), і навпаки.
для комплексних матриць перетворює косоермітову матрицю S (таку що, S^* = −S) в унітарну матрицю Q (таку що, Q^*Q = I), і навпаки.

\ Q=(I-S)(I+S)^{-1}

\ S=(I-Q)(I+Q)^{-1}

В випадку 2×2, отримаємо

{\begin{bmatrix}0&\tan {\frac {\theta }{2}}\\-\tan {\frac {\theta }{2}}&0\end{bmatrix}}\leftrightarrow {\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}.

Матриця повороту на 180°, не входить, оскільки tan ^θ⁄₂ прямує до нескінченності.

Для випадку 3×3, отримаємо

{\begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0\end{bmatrix}}\leftrightarrow {\frac {1}{K}}{\begin{bmatrix}w^{2}+x^{2}-y^{2}-z^{2}&2(xy-wz)&2(wy+xz)\\2(xy+wz)&w^{2}-x^{2}+y^{2}-z^{2}&2(yz-wx)\\2(xz-wy)&2(wx+yz)&w^{2}-x^{2}-y^{2}+z^{2}\end{bmatrix}},\qquad K=w^{2}+x^{2}+y^{2}+z^{2},\quad w=1.

Права частина це матриця повороту задану кватерніоном $\ w+x\mathbf {i} +y\mathbf {j} +z\mathbf {k} .$

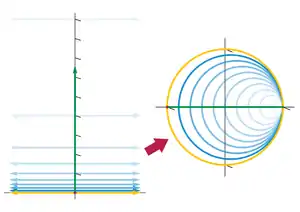
Перетворення Келі верхньої півплощини в одиничний круг

Перетворення Келі в комплексному аналізі це відображення комплексної площини в себе, заданої як

\operatorname {W} \colon z\mapsto {\frac {z-\mathbf {i} }{z+\mathbf {i} }}

Це відображення може бути розширене до автоморфізма Ріманової сфери.

{\begin{aligned}U&{}=(A-\mathbf {i} I)(A+\mathbf {i} I)^{-1}\\A&{}=\mathbf {i} (I+U)(I-U)^{-1}\end{aligned}}

...

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.