Розшарований кодобуток

Розшарований кодобуток (також розшарована сума, амальгама) — поняття в теорії категорій, двоїсте поняттю розшарованого добутку. Розшарований кодобуток єкограницею діаграми, що складається із двох морфізмів $f : Z \to X, g : Z \to Y$ . Він складається з об'єкта P і двох морфізмів X → P і Y → P, що разом із початковими морфізмами утворюють діаграму, що називається кодекартовим квадратом.

Означення

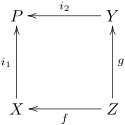
Нехай $f : Z \to X, g : Z \to Y$ — морфізми в категорії $C$ . Розшарованим кодобутком для пари морфізмів $(f, g)$ називається об'єкт P і морфізми i₁ : X → P і i₂ : Y → P для яких діаграма нижче є комутативною:

Окрім того P є універсальним серед об'єктів з цією властивістю. А саме, для будь-якого об'єкта $Q$ з морфізмами $j 1, j 2$ , які доповнюють $f, g$ до комутативного квадрата, існує єдиний морфізм $u : P \to Q$ , для якого діаграма нижче є комутативною:

Для розшарованого кодобутку часто використовуються позначення $P=X\sqcup _{Z}Y$ або $P=X+_{Z}Y$ .

Як і будь-які універсальні конструкції, розшарований кодобуток не обов'язково існує, але якщо існує, то визначений з точністю до ізоморфізму.

Приклади

У категорії множин $X\sqcup _{Z}Y$ — диз'юнктне об'єднання $X$ і $Y$ , в якому ототожнюються елементи із однаковим прообразом в $Z$ . Більш точно, $X\sqcup _{Z}Y=X\sqcup Y{\big /}\sim ,$ де $~$ — найменше відношення еквівалентності, таке що $i 1 \circ f (z) ~ i 2 \circ g (z)$ .

Конструкція склеювання просторів є прикладом побудови розшарованого кодобутку в категорії топологічних просторів. Більш детально, якщо $Z$ — підпростір у $Y$ і $g : Z \to Y$ — відповідне відображення включення, то можна «склеїти» $Y$ з $X$ по $Z$ , використовуючи «відображення відповідності» $f : Z \to X$ . Одержаний в результаті склеєний простір $X\cup _{f}Y$ є розшарованим кодобутком $X$ і $Y$ .

Окремим випадком попереднього прикладу є букет просторів X і Y з виділеними точками, де Z є одноточковим простором. Тоді розшарований кодобуток є рівним $X\vee Y$ , простору отриманому ідентифікацією виділених точок просторів X і Y.

В категорії абелевих груп розшаровані кодобутки можна розглядати як прямий сумі абелевих груп «зі склеюванням». А саме, якщо $f$ і $g$ — гомоморфізми із спільною областю визначення $Z$ , то розшарований кодобуток є факторгрупою прямої суми по підгрупі, породженій всіма елементами виду $(f (z), - g (z))$ . Приблизно те ж саме можна зробити в категорії модулів.

У категорії груп розшарований кодобуток називається вільним добутком з амальгамацією.

У категорії комутативних кілець розшарованим кодобутком кілець A, B і гомоморфізмів f : C → A і g : C → B є тензорний добуток кілець $A\otimes _{C}B$ із морфізмами $g':A\rightarrow A\otimes _{C}B$ і $f':B\rightarrow A\otimes _{C}B$ для яких $f'\circ g=g'\circ f$ .

Властивості

Якщо існує розшарований кодобуток A⊔_CB, то існує також розшарований кодобуток B⊔_CA і натуральний ізоморфізм A∪_CB ≅ B∪_CA.
В абелевій категорії всі кодобутки існують і вони зберігають коядра, а саме якщо (P, i₁, i₂) є розшарованим кодобутком f : Z → X і g : Z → Y, тоді натуральні перетворення coker(f) → coker(i₂) і coker(g) → coker(i₁) є ізоморфізмами.
Існує натуральний ізоморфізм (A⊔_CB)⊔_B D ≅ A⊔_CD. Більш детально:
- якщо задано морфізми f : C → A, g : C → B і h : B → D і
- розшарований кодобуток f і g задано як i : A → P і j : B → P, і
- розшарований кодобуток j і h задано як k : P → Q і l : D → Q ,
- тоді розшарований кодобуток f і hg задано як ki : A → Q і l : D → Q.

Графічно це означає, що два кодекартові квадрати розташовані поруч, із одним спільним морфізмом, утворюють більший кодекартів квадрат, якщо ігнорувати спільний морфізм.

Кодобутки є розшарованими кодобутками із початкового об'єкта; ковирівнювач морфізмів f, g : X → Y є розшарованим кодобутком [f, g] і [1_X, 1_X], тому якщо в категорії є початковий об'єкт і визначені всі розшаровані кодобутки, тоді в ній існують кодобутки і ковирівнювачі.
Натомість розшарований кодобуток f : Z → X і g : Z → Y можна отримати через кодобутки і ковирівнювачі. Для цього спершу вводиться кодобуток X і Y. Тоді можна розглядати два морфізми із Z у цей кодобуток: морфізм одержаний композицією f і стандартного морфізму з X у кодобуток і морфізм одержаний композицією g і стандартного морфізму з Y у кодобуток. Розшарований кодобуток f і g є рівним ковирівнювачу цих морфізмів.

Див. також

Література

Adámek, Jiří, Herrlich, Horst, & Strecker, George E.; (1990). Abstract and Concrete Categories (4.2MB PDF). John Wiley & Sons. ISBN 0-471-60922-6.
Leinster, Tom (2014). Basic Category Theory. Cambridge Studies in Advanced Mathematics 143. Cambridge University Press. ISBN 978-1-107-04424-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.