J-інваріант

Мотивацією для означення j-інваріанта є вивчення класів ізоморфності еліптичних кривих. Кожна еліптична крива E над полем C є комплексним тором і тому її можна ідентифікувати з ґраткою порядку 2, тобто двовимірною ґраткою в C. Як виявляється множення ґратки на комплексне число, що відповідає повороту і розтягуванню ґратки, не змінює клас ізоморфності еліптичних кривих і тому можна розглядати лише ґратки породжені 1 і деяким τ в H (де H — верхня комплексна півплощина). Навпаки, якщо визначити

${\displaystyle {\begin{aligned}g_{2}&=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},\\g_{3}&=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6},\end{aligned}}}$

то ця ґратка визначає еліптичну криву над C задану рівнянням y² = 4x³ − g₂x - g₃.

j-інваріант за означенням рівний

${\displaystyle j(\tau )=1728{\frac {g_{2}^{3}}{\Delta }}}$

де модулярний дискримінант Δ рівний

${\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}}$

Δ є модулярною формою ваги, g₂ — модулярною формою ваги 4, тож її 3-й степінь теж є модулярною формою ваги 12. Тому їх частка, а відповідно і функція j, є модулярною функцією інваріантною щодо дії групи SL(2, Z). j є бієкцією між класами ізоморфності еліптичних кривих над C і комплексними числами.

Фундаментальний регіон модулярної групи на верхній півплощині.

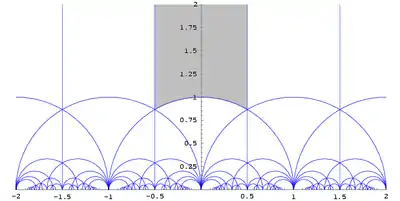
Перетворення τ → τ + 1 і τ → -τ⁻¹ разом породжують групу, що називається модулярною групою. Вибравши необхідне перетворення з цієї групи,

${\displaystyle \tau \mapsto {\frac {a\tau +b}{c\tau +d}},\qquad ad-bc=1,}$

для будь-якого τ можна знайти значення змінної з тим самим значенням функції j, що лежить в фундаментальному регіоні для j, тобто підмножини комплексних чисел, що задовольняють умови:

${\displaystyle {\begin{aligned}|\tau |&\geq 1\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )\leq {\tfrac {1}{2}}\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )<0\Rightarrow |\tau |>1\end{aligned}}}$

Функція j(τ) на цьому регіоні приймає кожне значення з C точно один раз. Тобто для кожного c в C,є єдине число τ в фундаментальному регіоні для якого c = j(τ).

Як поверхня Рімана, фундаментальний регіон має рід 0, і всі множина модулярних функцій рівна множині раціональних функцій від j(τ) тобто C(j).

Багато важливих властивостей j пов'язані з q-розкладом (рядом Фурє), тобто розкладом в ряд Лорана щодо змінної q = exp(2πiτ),що починається як:

${\displaystyle j(\tau )={1 \over q}+744+196884q+21493760q^{2}+864299970q^{3}+20245856256q^{4}+\cdots }$

Зокрема звідси видно, що оскільки j має простий полюс в каспі,то q-розклад не має членів степенів нижчих, ніж q⁻¹.

Асимптотично коефцієнти біля qⁿ рівні

${\displaystyle {\frac {e^{4\pi {\sqrt {n}}}}{{\sqrt {2}}n^{3/4}}}}$,

що випливає з використання методу Харді — Літлвуда.[1][2]

Справедливою є формула

${\displaystyle j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}}$

де x = λ(1−λ) і λ є модулярною ламбда-функцією

${\displaystyle \lambda (\tau )={\frac {\theta _{2}^{4}(0,\tau )}{\theta _{3}^{4}(0,\tau )}}=k^{2}(\tau )}$

часткою тета-функцій Якобі ${\displaystyle \theta _{m}}$, і квадратом еліптичного модуля ${\displaystyle k(\tau )}$.[3] Значення j не змінюється коли λ замінити на якісь значення з множини:[4]

${\displaystyle \left\lbrace {\lambda ,{\frac {1}{1-\lambda }},{\frac {\lambda -1}{\lambda }},{\frac {1}{\lambda }},{\frac {\lambda }{\lambda -1}},1-\lambda }\right\rbrace }$

Нехай ${\displaystyle q=e^{\pi i\tau }}$ і тета-функція Якобі визначена як

${\displaystyle \vartheta (0;\tau )=\vartheta _{00}(0;\tau )=1+2\sum _{n=1}^{\infty }\left(e^{\pi i\tau }\right)^{n^{2}}=\sum _{n=-\infty }^{\infty }q^{n^{2}}}$

і подібно інші тета-функції Якобі. Нехай:

${\displaystyle {\begin{aligned}a&=\theta _{2}(0;q)=\vartheta _{10}(0;\tau )\\b&=\theta _{3}(0;q)=\vartheta _{00}(0;\tau )\\c&=\theta _{4}(0;q)=\vartheta _{01}(0;\tau )\end{aligned}}}$

Тоді ${\displaystyle a^{4}-b^{4}+c^{4}=0}$ і можна записати

${\displaystyle {\begin{aligned}g_{2}(\tau )&={\tfrac {2}{3}}\pi ^{4}\left(a^{8}+b^{8}+c^{8}\right)\\g_{3}(\tau )&={\tfrac {4}{27}}\pi ^{6}{\sqrt {\frac {(a^{8}+b^{8}+c^{8})^{3}-54(abc)^{8}}{2}}}\\\Delta &=g_{2}^{3}-27g_{3}^{2}=(2\pi )^{12}\left({\tfrac {1}{2}}abc\right)^{8}=(2\pi )^{12}\eta (\tau )^{24}\end{aligned}}}$

де η(τ) — ета функція Дедекінда. Тоді j(τ) можна записати у формі зручній для обчислень через швидку збіжність:

${\displaystyle j(\tau )=1728{\frac {g_{2}^{3}}{g_{2}^{3}-27g_{3}^{2}}}=32{(a^{8}+b^{8}+c^{8})^{3} \over (abc)^{8}}}$

Вище j означалася як функція комплексної змінної. Проте як інваріант класів ізоморфності еліптичних кривих, її можна визначити алгебраїчно. Нехай

${\displaystyle y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}$

є еліптичною кривою над довільним полем. Позначимо

${\displaystyle b_{2}=a_{1}^{2}+4a_{2},\quad b_{4}=a_{1}a_{3}+2a_{4}}$

${\displaystyle b_{6}=a_{3}^{2}+4a_{6},\quad b_{8}=a_{1}^{2}a_{6}-a_{1}a_{3}a_{4}+a_{2}a_{3}^{2}+4a_{2}a_{6}-a_{4}^{2}}$

${\displaystyle c_{4}=b_{2}^{2}-24b_{4},\quad c_{6}=-b_{2}^{3}+36b_{2}b_{4}-216b_{6}}$

і

${\displaystyle \Delta =-b_{2}^{2}b_{8}+9b_{2}b_{4}b_{6}-8b_{4}^{3}-27b_{6}^{2}}$ позначення для дискримінпіпіанта

${\displaystyle j={c_{4}^{3} \over \Delta }}$

Якщо поле над яким визначена крива має характеристику не рівну 2 чи 3,означення можна переписати як

${\displaystyle j=1728{c_{4}^{3} \over c_{4}^{3}-c_{6}^{2}}}$

Нижче наведені значення в окремих точках функції ${\displaystyle J(\tau )\equiv j(\tau )/1728}$

${\displaystyle {\begin{aligned}J(i)&=J\left({\tfrac {1+i}{2}}\right)=1\\J\left({\sqrt {2}}i\right)&=\left({\tfrac {5}{3}}\right)^{3}\\J(2i)&=\left({\tfrac {11}{2}}\right)^{3}\\J\left(2{\sqrt {2}}i\right)&={\tfrac {125}{216}}\left(19+13{\sqrt {2}}\right)^{3}\\J(4i)&={\tfrac {1}{64}}\left(724+513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2i}{2}}\right)&={\tfrac {1}{64}}\left(724-513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&={\tfrac {125}{216}}\left(19-13{\sqrt {2}}\right)^{3}\\J(3i)&={\tfrac {1}{27}}\left(2+{\sqrt {3}}\right)^{2}\left(21+20{\sqrt {3}}\right)^{3}\\J\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\J\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {64000}{7}}\left(651+142{\sqrt {21}}\right)^{3}\\J\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\J\left({\sqrt {21}}i\right)&={\tfrac {1}{32}}\left(5+3{\sqrt {3}}\right)^{2}\left(3+{\sqrt {7}}\right)^{2}\left(65+34{\sqrt {3}}+26{\sqrt {7}}+15{\sqrt {21}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{1}}\right)&={\tfrac {1}{16}}\left(10+7{\sqrt {2}}+4{\sqrt {5}}+3{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{2}}\right)&={\tfrac {1}{16}}\left(10+7{\sqrt {2}}-4{\sqrt {5}}-3{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{5}}\right)&={\tfrac {1}{16}}\left(10-7{\sqrt {2}}+4{\sqrt {5}}-3{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{10}}\right)&={\tfrac {1}{16}}\left(10-7{\sqrt {2}}-4{\sqrt {5}}+3{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {1+{\sqrt {31}}i}{2}}\right)&=\left(1-\left(1+{\frac {\sqrt {19}}{2}}\left({\sqrt {\tfrac {13-{\sqrt {93}}}{13+{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}+{\sqrt {27}}}{{\sqrt {31}}-{\sqrt {27}}}}}+{\sqrt {\tfrac {13+{\sqrt {93}}}{13-{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}-{\sqrt {27}}}{{\sqrt {31}}+{\sqrt {27}}}}}\right)\right)^{2}\right)^{3}\\J({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\J(7i)&=\left(1+{\tfrac {9}{4}}{\sqrt {21+8{\sqrt {7}}}}\left(30+11{\sqrt {7}}+\left(6+{\sqrt {7}}\right){\sqrt {21+8{\sqrt {7}}}}\right)^{2}\right)^{3}\\J(8i)&=\left(1+{\tfrac {9}{4}}{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}\right)\left(123+104{\sqrt[{4}]{2}}+88{\sqrt {2}}+73{\sqrt[{4}]{8}}\right)^{2}\right)^{3}\\J(10i)&=\left(1+{\tfrac {9}{8}}\left(2402+1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}+719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i}{2}}\right)&=\left(1+{\tfrac {9}{8}}\left(2402-1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}-719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J(2{\sqrt {58}}i)&=\left(1+{\tfrac {9}{256}}\left(1+{\sqrt {2}}\right)^{5}\left(5+{\sqrt {29}}\right)^{5}\left(793+907{\sqrt {2}}+237{\sqrt {29}}+103{\sqrt {58}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left(9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left(22297077+9971556{\sqrt {5}}+\left(3571365+1597163{\sqrt {5}}\right){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right)^{2}\right)^{3}\\\end{aligned}}}$

Кілька спеціальних значень були розраховані в 2014 році:[6]

${\displaystyle {\begin{aligned}J\left({\tfrac {5i+1}{2}}\right)&=\left({\frac {2927-1323{\sqrt {5}}}{2}}\right)^{3},\\J(5i)&=\left({\frac {2927+1323{\sqrt {5}}}{2}}\right)^{3},\\\end{aligned}}}$

для значень нижче використані позначення,

${\displaystyle {\begin{aligned}a_{1},a_{2},a_{3},a_{4}&=1190448488,858585699,540309076,374537880\\b_{1},b_{2},b_{3},b_{4}&=693172512,595746414,407357424,240819696\end{aligned}}}$

${\displaystyle {\begin{aligned}J\left({\tfrac {5i+2}{4}}\right)&=\left({\frac {\left(1+{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}-a_{2}{\sqrt {2}}+a_{3}{\sqrt {5}}-a_{4}{\sqrt {10}}-{\sqrt[{4}]{5}}\left(b_{1}-b_{2}{\sqrt {2}}+b_{3}{\sqrt {5}}-b_{4}{\sqrt {10}}\right)\right)\right)^{3},\\J\left({\tfrac {10i+1}{2}}\right)&=\left({\frac {\left(1+{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}-a_{2}{\sqrt {2}}+a_{3}{\sqrt {5}}-a_{4}{\sqrt {10}}+{\sqrt[{4}]{5}}\left(b_{1}-b_{2}{\sqrt {2}}+b_{3}{\sqrt {5}}-b_{4}{\sqrt {10}}\,\right)\right)\right)^{3},\\J\left({\tfrac {5i}{4}}\right)&=\left({\frac {\left(1+{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}+a_{2}\,{\sqrt {2}}+a_{3}{\sqrt {5}}+a_{4}{\sqrt {10}}-{\sqrt[{4}]{5}}\left(b_{1}+b_{2}{\sqrt {2}}+b_{3}{\sqrt {5}}+b_{4}{\sqrt {10}}\right)\right)\right)^{3},\\J(20i)&=\left({\frac {\left(1+{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}+a_{2}{\sqrt {2}}+a_{3}{\sqrt {5}}+a_{4}{\sqrt {10}}+{\sqrt[{4}]{5}}\left(b_{1}+b_{2}{\sqrt {2}}+b_{3}{\sqrt {5}}+b_{4}{\sqrt {10}}\right)\right)\right)^{3}.\end{aligned}}}$

${\displaystyle J\left({\tfrac {1}{4}}(5i\pm 1)\right)=\left(1-{\tfrac {9}{8}}\left((2402-1074{\sqrt {5}})i\pm (1607-719{\sqrt {5}}){\sqrt[{4}]{5}}\right)^{2}\right)^{3}.}$

Ще чотири спеціальні значення наведені у вигляді двох комплексно-сполучених пар:[7]

${\displaystyle {\begin{aligned}J\left({\tfrac {4}{13}}\left(5i\pm 1\right)\right)=\left({\frac {\left(1-{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}-a_{2}{\sqrt {2}}-a_{3}{\sqrt {5}}+a_{4}{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(b_{1}-b_{2}{\sqrt {2}}-b_{3}{\sqrt {5}}+b_{4}{\sqrt {10}}\right)\right)\right)^{3},\\J\left({\tfrac {5}{17}}\left(4i\pm 1\right)\right)=\left({\frac {\left(1-{\sqrt {5}}\right)^{37}}{2^{39}}}\left(a_{1}+a_{2}{\sqrt {2}}-a_{3}{\sqrt {5}}-a_{4}{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(b_{1}+b_{2}{\sqrt {2}}-b_{3}{\sqrt {5}}-b_{4}{\sqrt {10}}\right)\right)\right)^{3}\end{aligned}}}$

• Еліптична крива
• Еліптична функція
• Модулярна форма

• Apostol, Tom M. (1976). Modular functions and Dirichlet Series in Number Theory. Graduate Texts in Mathematics 41. New York: Springer-Verlag. MR 0422157..
• Berndt, Bruce C.; Chan, Heng Huat (1999). Ramanujan and the modular j-invariant. Canadian Mathematical Bulletin 42 (4): 427–440. MR 1727340. doi:10.4153/CMB-1999-050-1. Архів оригіналу за 29 вересня 2007. Процитовано 25 лютого 2017.
• Cox, David A. (1989). Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication. New York: Wiley-Interscience Publication, John Wiley & Sons Inc. MR 1028322.
• Conway, John Horton; Norton, Simon (1979). Monstrous moonshine. Bulletin of the London Mathematical Society 11 (3): 308–339. MR 0554399. doi:10.1112/blms/11.3.308.
• Rankin, Robert A. (1977). Modular forms and functions. Cambridge: Cambridge University Press. ISBN 0-521-21212-X. MR 0498390.
• Schneider, Theodor (1937). Arithmetische Untersuchungen elliptischer Integrale. Math. Annalen 113: 1–13. MR 1513075. doi:10.1007/BF01571618..