Багатозначна функція

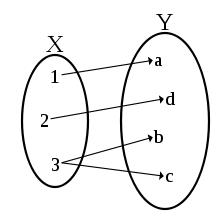
Функція ${\displaystyle F}$, яка кожному елементу множини ${\displaystyle X}$ ставить у відповідність деяку підмножину множини ${\displaystyle Y,}$ називається багатозначною функцією[2], якщо хоча б для одного ${\displaystyle x\in X}$ значення ${\displaystyle F(x)}$ містить більше одного елемента ${\displaystyle Y.}$

Звичайні (однозначні) функції можна розглядати як окремий випадок багатозначних, у яких значення складається рівно з одного елемента.

Найпростіший приклад — двозначна функція квадратного кореня з додатного числа, у неї два значення, що розрізняються знаком. Наприклад, квадратний корінь з 16 має два значення — ${\displaystyle +4}$ і ${\displaystyle -4.}$

Інший приклад — обернені тригонометричні функції (наприклад, арксинус) — оскільки значення прямих тригонометричних функцій повторюються з періодом ${\displaystyle 2\pi }$ або ${\displaystyle \pi ,}$ то значення обернених функцій багатозначні («нескінченнозначні»), всі вони мають вигляд ${\displaystyle \varphi +2k\pi }$ або ${\displaystyle \varphi +k\pi ,}$ де ${\displaystyle k}$ — довільне ціле число.

Багатозначні функції незручно використовувати у формулах, тому з їх значень нерідко виділяють одне, яке називають головним. Для квадратного кореня це додатне значення, для арксинуса — значення, що потрапляє в інтервал ${\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$ тощо.

Первісну функцію (невизначений інтеграл) також можна розглядати як нескінченнозначну функцію, оскільки вона визначена з точністю до сталої інтегрування.

Характерний приклад багатозначних функцій — деякі аналітичні функції в комплексному аналізі. Неоднозначність виникає при аналітичному продовженні за різними шляхами. Також часто багатозначні функції виходять як результат взяття обернених функцій.

Наприклад, корінь n-го степеня з будь-якого ненульового комплексного числа набуває рівно ${\displaystyle n}$ значень. У комплексного логарифма число значень нескінченне, одне з них оголошено головним.

У комплексному аналізі поняття багатозначної функції тісно пов'язане з поняттям ріманової поверхні — поверхні в багатовимірному комплексному просторі, на якій дана функція стає однозначною.

• Багатозначне відображення

• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд. — М. : Наука, 1972.
• Шабат Б. В. Введение в комплексный анализ. — М. : Наука, 1969. — 577 с.