Біраціональна геометрія
Біраціональна геометрія — це розділ алгебричної геометрії, основним завданням якого є класифікація алгебричних многовидів з точністю до біраціональної еквівалентності[1]. Зводиться до вивчення відображень, задаваних раціональними функціями, а не многочленами. Відображення може бути не визначеним у деяких точках, які є полюсами раціональної функції.
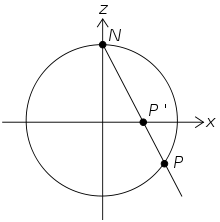
Біраціональні відображення
Раціональне відображення одного (незвідного) многовиду X в інший многовид Y (записується як пунктирна стрілка X ⇢ Y) визначається як морфізм з непорожньої відкритої підмножини U многовиду X в Y. За визначенням топології Зариського, використовуваної в алгебричній геометрії, непорожня відкрита підмножина U є завжди доповненням підмножини X меншої розмірності. Конкретно, раціональне відображення можна записати в координатах з використанням раціональних функцій.
Біраціональне відображення із X в Y — це раціональне відображення f: X ⇢ Y таке, що існує раціональне відображення Y ⇢ X, обернене до f. Біраціональне відображення породжує ізоморфізм непорожньої відкритої підмножини X у непорожній відкритій підмножині Y. У цьому випадку кажуть, що X і Y біраціонально еквівалентні. В алгебричних термінах два многовиди над полем k біраціонально еквівалентні тоді і тільки тоді, коли їхні поля функций ізоморфні як розширення поля k.
Особливий випадок — біраціональний морфізм f: X → Y, що означає морфізм, який є біраціональним. Тоді f визначена на всьому X, але її зворотна може бути визначена не на всьому Y. Зазвичай це трапляється, коли біраціональний морфізм стискає деякі підмноговиди X у точки в Y.
Кажуть, що многовид X раціональний, якщо він раціонально еквівалентний афінному простору (або, еквівалентно, проєктивному простору) тієї ж розмірності. Раціональність є цілком природною властивістю — вона означає, що X без деякої підмножини меншої розмірності можна ототожнити з афінним простором без деякої підмножини меншої розмірності. Наприклад, коло, задане рівнянням x2 + y2 — 1 = 0, є раціональною кривою, оскільки формули
визначають біраціональне відображення прямої в коло. (Якщо підставляти замість t раціональні числа, одержимо піфагорові трійки.) Зворотне відображення переводить (x,y) в (1 − y)/x.
Загальніше, гладка квадратична (степеня 2) гіперповерхня X будь-якої розмірності n є раціональною через стереографічну проєкцію (для квадратичного многовиду X над полем k має передбачатися, що він має k-раціональну точку. Це виконується автоматично, якщо k алгебрично замкнуте.). Щоб визначити стереографічну проєкцію, припустимо, що p — точка в X. Тоді біраціональне відображення з X у проєктивний простір Pn прямих, що проходять через p, задається відображенням точки q в X у пряму, що проходить через p і q. Це відображення є біраціональною еквівалентністю, але не ізоморфізмом многовиду, оскільки воно не визначене при q = p (і зворотне відображення не визначене для прямих, що проходять через p і лежать в X).
Мінімальні моделі і розв'язання особливих точок
Будь-який алгебричний многовид біраціонально еквівалентний проєктивному многовиду (лема Чжоу). Отже, для біраціональної класифікації достатньо працювати лише з проєктивними многовидами, і це зазвичай найзручніший вибір.
Значно глибше, за теоремою Хіронаки про розв'язання особливих точок — над полем характеристики 0 (такому, як комплексні числа) будь-який многовид є біраціонально еквівалентним гладкому проєктивному многовиду. З урахуванням цього, достатньо класифікувати гладкі проєктивні многовиди з точністю до біраціональної еквівалентності.
У розмірності 1, якщо дві гладкі проєктні криві біраціонально еквівалентні, вони ізоморфні. Однак це не так у розмірності 2 і вище через конструкцію роздуття. При роздутті будь-який гладкий проєктивний многовид розмірності 2 і вище біраціонально еквівалентний нескінченному числу «більших» многовидів, наприклад, з більшими числами Бетті.
Це приводить до ідеї мінімальних моделей — чи існує єдиний найпростіший многовид у кожному класі рацінальної еквівалентності? Сучасне визначення мінімальної моделі — проєктивний многовид мінімальний, якщо канонічне лінійне розшарування має невід'ємний степінь на будь-якій кривій в . Іншими словами, є неф-розшаруванням. Легко перевірити, що роздуті многовиди ніколи не бувають мінімальними.
Ця ідея добре працює для алгебричних поверхонь (многовидів розмірності 2). У сучасних термінах центральним результатом італійської школи алгебричної геометрії 1890—1910 років, частиною класифікації, став факт, що будь-яка поверхня біраціонально еквівалентна або добутку для деякої кривої , або мінімальної поверхні [2]. Ці два випадки взаємно виключають один одного і унікальна, якщо існує. Якщо існує, її називають мінімальною моделлю поверхні .
Біраціональні інваріанти
Перш за все, не цілком зрозуміло, як показати, що існує якась нераціональна алгебрична поверхня. Для того, щоб це довести, потрібно використати деякі інваріанти алгебричних многовидів.
Один корисний набір біраціональних інваріантів — плюрироди. Канонічне розшаровання гладкого многовиду розмірності — це лінійне розшаровання -форма , яке є -им зовнішнім степенем канонічного розшаровання многовиду X. Для цілого числа , -й тензорний степінь знову є лінійним розшарованням. Для векторний простір глобальних перетинів має чудову властивість, що біраціональне відображення : ⇢ між гладкими проєктивними многовидами породжує ізоморфізм ≅[3].
Для d ≥ 0 визначимо d-ий плюрирод Pd як розмірність векторного простору H0(X, KXd). Тоді плюрироди є біраціональними інваріантами гладких проєктивних многовидів. Зокрема, якщо який-небудь плюрирод Pd при d>0 не дорівнює нулю, то X не є раціональним многовидом.
Фундаментальним біраціональним інваріантом є розмірність Кодайри, яка вимірює зростання плюриродів Pd при d, що прямує до нескінченності. Розмірність Кодайри ділить всі многовиди розмірності n на n+2 типи з розмірностями Кодайри -∞, 0, 1, …, n. Цей інваріант показує складність многовиду, при цьому проєктивний простір має розмірність Кодайри −∞. Найскладніші многовиди — це ті, у яких розмірність Кодайри збігається з розмірністю простору n, і ці многовиди мають назву многовиди загального типу.
Загальніше, для будь-якого натурального прямого доданка E(Ω1) r-го тензорного степеня кодотичного пучка Ω1 з r ≥ 0 векторний простір глобальних перетинів H0(X, E(Ω1)) є біраціональним інваріантом для гладких проєктивних многовидів. Зокрема, числа Годжа hr,0 = dim H0(X, Ωr) є біраціональними інваріантами X. (Більшість інших чисел Годжа hp, q не є біраціональними інваріантами, що показується роздуттям.)
Фундаментальна група π1(X) є біраціональним інваріантом для гладких комплексних проєктивних многовидів.
«Теорема про слабку факторизацію», яку довели Абрамович, Кару, Мацукі і Влодарчик[4], стверджує, що будь-яке біраціональне відображення між двома гладкими комплексними проєктивними многовидами можна розкласти на скінченне число роздуттів або здуттів гладких підмноговидів. Це важливо знати, однак залишається складною задача визначення, чи є два гладких проєктивних многовиди біраціонально еквівалентними.
Мінімальні моделі у вищих розмірностях
Проєктивний многовид X називають мінімальним, якщо канонічне розшарування KX є неф-розшаруванням. Для X розмірності 2 достатньо розглядати гладкі многовиди. У розмірностях 3 і вище мінімальним многовидам має бути дозволено мати деякі слабкі особливості, для яких поведінка KX залишається хорошою. Їх називають термінальними особливостями.
Проте, з істинності гіпотези про мінімальну модель випливало б, що будь-який многовид X або покривається раціональними кривими, або біраціонально еквівалентний мінімальному многовиду Y. Якщо таке існує, то Y називають мінімальною моделлю многовиду X.
Мінімальні моделі не єдині в розмірності 3 і вище, але будь-які два мінімальних біраціональних многовиди дуже близькі. Наприклад, вони ізоморфні поза підмножинами з коефіцієнтом 2 і вище, і, точніше, вони пов'язані послідовністю фліпів. Отже, гіпотеза про мінімальну модель давала б істотну інформацію про біраціональну класифікацію алгебричних многовидів.
Морі довів гіпотезу для розмірності 3[5]. Існує значний прогрес у вищих розмірностях, хоча головна проблема залишається відкритою. Зокрема, Біркар, Кассіні, Гакон і Маккернан[6] довели, що будь-який многовид загального типу над полем характеристики 0 має мінімальну модель.
Унілінійчаті многовиди
Многовид називають унілінійчатим, якщо він покритий раціональними кривими. Унілінійчатий многовид не має мінімальної моделі, але існує хороша заміна — Біркар, Кассіні, Гакон і Маккернан показали, що будь-який унілінійчатий многовид над полем з нульовою характеристикою є біраціональним розшаруванням Фано[7]. Це веде до задачі біраціональної класифікації розшарувань Фано і (як найцікавіший випадок) многовидів Фано. За визначенням, проєктивний многовид X є многовидом Фано, якщо антиканонічний пучок KX* є рясним. Многовиди Фано можна розглядати як найближчі до проєктивних просторів.
У розмірності 2 будь-який многовид Фано (відомий як поверхня дель Пеццо) над алгебрично замкнутим полем раціональний. Головним відкриттям 1970-х років було те, що, починаючи з розмірності 3, існує багато многовидів Фано, які не є раціональними. Зокрема, гладкі кубічні тривимірні многовиди, за Клеменсом і Ґріффітсом[8], не раціональні, а гладкі тривимірні многовиди четвертого степеня не раціональні за Ісковських і Маніним[9]. Все ж, задача точного визначення, які многовиди Фано раціональні, далека від розв'язання. Наприклад, невідомо, чи існує нераціональна гладка кубічна гіперповерхня в Pn+1 з n ≥ 4.
Групи біраціональних автоморфізмів
Алгебричні многовиди значно відрізняються за кількістю їхніх біраціональних автоморфізмів. Будь-який многовид загального типу дуже жорсткий у тому сенсі, що його група біраціональних автоморфізмів скінченна. Інша крайність, група біраціональних автоморфізмів проєктивного простору Pn над полем k, відома як група Кремони Crn(k), велика (має нескінченну розмірність) для n ≥ 2. Для n = 2 комплексна група Кремони Cr2(C) породжується «квадратичним перетворенням»: [x,y,z] ↦ [1/x, 1/y, 1/z]
разом з групою PGL(3,C) автоморфізм P2, за Максом Нетером і Гвідо Кастельнуово. На відміну від цього, група Кремони в розмірності n ≥ 3 дуже таємнича, для неї не відомо явної множини генераторів.
Ісковських і Манін[9] показали, що група біраціональних автоморфізмів гладких гіперповерхонь четвертого порядку (квартик) тривимірних многовидів дорівнює її групі автоморфізмів, яка скінченна. У цьому сенсі тривимірні многовиди четвертого порядку далекі від раціональності, оскільки група біраціональних автоморфізмів раціонального многовиду величезна. Цей феномен «біраціональної жорсткості» відкрито відтоді для багатьох розшарованих просторів Фано.
Примітки
- Долгачёв, Исковских, 1977, с. 463.
- Kollár, Mori, 1998, с. Theorem 1.29.
- Hartshorne, 1977, с. Exercise II.8.8.
- Abramovich, Karu, Matsuki, Włodarczyk, 2002.
- Mori, 1988.
- Birkar, Cascini, Hacon, McKernan, 2010.
- (Birkar, Cascini, Hacon, McKernan, 2010); З наслідку 1.3.3 випливає, що будь-який унілінійчатий многовид у нульовій характеристиці є біраціональним розшаруванню Фано, якщо використати простий факт, що унілінійчатий многовид X покривається сімейством кривих, для яких KX має від'ємний степінь. Зазначене твердження можна знайти в книзі Дебарре (Debarre, 2001), Наслідок 4.11 і Приклад 4.7(1).
- Clemens, Griffiths, 1972.
- Исковских, Манин, 1971, с. 140—166.
Література
- И. В. Долгачёв, В. А. Исковских. Математическая Энциклопедия / И. М. Виноградов. — М. : «Советская Энциклопедия», 1977. — Т. 1 (А – Г).
- Dan Abramovich, Kalle Karu, Kenji Matsuki, Jarosław Włodarczyk. Torification and factorization of birational maps // Journal of the American Mathematical Society. — 2002. — Vol. 15, iss. 3 (17 February). — P. 531–572. — DOI:.
- Caucher Birkar, Paolo Cascini, Christopher D. Hacon, James McKernan. Existence of minimal models for varieties of log general type // Journal of the American Mathematical Society. — 2010. — Vol. 23, iss. 2 (17 February). — P. 405–468. — arXiv:math.AG/0610203. — DOI:.
- C. Herbert Clemens, Phillip A. Griffiths. The intermediate Jacobian of the cubic threefold // Annals of Mathematics. Second Series. — The Annals of Mathematics, Vol. 95, No. 2, 1972. — Т. 95, вип. 2 (17 лютого). — С. 281.356. — ISSN 0003-486X. — DOI:.
- Olivier Debarre. Higher-Dimensional Algebraic Geometry. — Springer-Verlag, 2001. — ISBN 0-387-95227-6.
- Phillip A. Griffiths, Joseph Harris. Principles of Algebraic Geometry. — John Wiley & Sons, 1978. — ISBN 0-471-32792-1.
- Robin Hartshorne. Algebraic Geometry. — Springer-Verlag, 1977. — ISBN 0-387-90244-9.
- В. А. Исковских, Ю. И. Манин. Трехмерные квартики и контрпримеры к проблеме Люрота // Матем. сб.. — 1971. — Т. 86 (128), № 1 (9) (17 лютого). — С. 140—166. — (Новая серия). — DOI:.
- János Kollár, Shigefumi Mori. Birational Geometry of Algebraic Varieties. — Cambridge University Press, 1998. — ISBN 0-521-63277-3.
- Shigefumi Mori. Flip theorem and the existence of minimal models for 3-folds // Journal of the American Mathematical Society. — American Mathematical Society, 1988. — Vol. 1, iss. 1 (17 February). — P. 117–253. — ISSN 0894-0347. — DOI:.
