Від'ємний біноміальний розподіл
Від’ємний біноміальний розподіл в теорії імовірностей — розподіл дискретної випадкової величини, рівної кількості невдач в послідовності випробувань Бернуллі з імовірністю успіху , проведеній до -го успіху.
| Від'ємний біноміальний розподіл | |
|---|---|
|
Функція ймовірностей 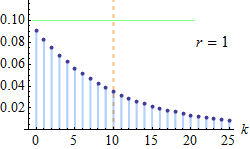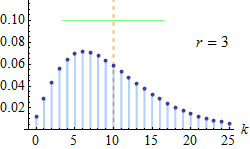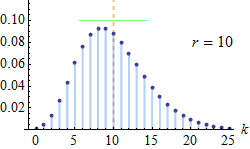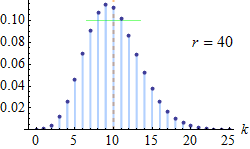 Помаранчева лінія показує математичне сподівання, яке для усіх малюнків дорівнює 10; зелена лінія показує стандартне відхилення. | |
| Параметри |
r > 0 — number of failures until the experiment is stopped (integer, but the definition can also be extended to reals) p ∈ [0,1] — ймовірність успіху в кожному випробуванні (дійсне число) |
| Носій функції | k ∈ { 0, 1, 2, 3, … } — число успіхів |
| Розподіл імовірностей | involving a binomial coefficient |
| Функція розподілу ймовірностей (cdf) | the regularized incomplete beta function |
| Середнє | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Твірна функція моментів (mgf) | |
| Характеристична функція | |
| Генератриса (pgf) | |
Означення
Нехай — послідовність незалежних випадкових величин з розподілом Бернуллі, тобто
Побудуємо випадкову величину наступним чином. Нехай — номер -го успіху в цій послідовності. Тоді . Більш строго, покладемо . Тоді
- .
Розподіл випадкової величини , визначеної таким чином, називається від’ємним біноміальним. Пишуть: .
Функції ймовірності і розподілу
Функція ймовірностей випадкової величини має вигляд:
- .
Функція розподілу кусково-постійна, і її значення в цілих точках може бути виражене через неповну бета-функцію:
- .
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
