ЕОМ (техніка)
Будь-яка цифрова Електронно-обчислювальна машина (скорочено ЕОМ) складається з логічних схем, які знаходяться в одному з двох станів - "логічний нуль" та "логічна одиниця". За логічні 0 та 1 можна прийняти будь-який вираз, у тому числі рядковий, який характеризується як "істина" або "хиба" (див. Булева алгебра).
У техніці 0 та 1 - це стан електричних схем з певними параметрами. Наприклад, для логічних елементів та схем, виконаних по технології транзисторно-транзисторної логіки, логічний 0 - це напруга у діапазоні 0...+4 В, а логічний 1 - це напруга у діапазоні +2,4...+5 В. Робота логічних схем описується посередництвом алгебри логіки (булевої алгебри), яка була розроблена Джорджем Булем (1845-1864) й є основою усіх методів спрощення булевих виразів.
Будь-яку інформацію можна представити за допомогою нулів та одиниць.
Інформаційна основа
У світі окрім енергії та речовини існує ще одна субстанція - інформація. Спочатку під інформацією розумілися відомості, які передавалися між людьми усним, писемним або іншим шляхом. Після робіт Н.Вігнера стало ясно, що інформаційні взаємодії існують не лише між людьми, але й властиві усім живим й неживим об'єктам. Нині вважається, що інформаційні взаємодії складають основу управління у системах будь-якої природи. При цьому розрізняють синтаксичний, семантичний й прагматичний аспекти інформації. Синтаксична сторона інформації характеризує план її виразу, склад, структуру, складність й організованість. Семантичний аспект інформації характеризує її змістове наповнення, зіставність з декотрими еталонними об'єктами та явищами. Прагматична сторона інформації характеризує її здатність впливати на процеси управління у системі з точки зору її цінності, корисності, або шкідливості, тобто ефект, який виникає внаслідок інформаційної взаємодії.
Інформація здатна змінювати фізичний вид її носія у процесі передачі від керуючої системи до керовного об'єкта (наприклад, голос, електромагнітні коливання, знову звукові сигнали голосу тощо). Інформація не підпорядковується законам збереження (вона не зменшується у джерела; її можна віддати, але не завжди можна забрати). Швидкість протікання інформаційних процесів не обмежена законами, які властиві матеріальним процесам. Також інформація здатна забезпечити випереджуюче відображення дійсності. Для інформації характерний "несиловий" спосіб впливу, коли відносно слабкі фізичні сигнали, які несуть інформацію, здійснюють сильний вплив на керовані процеси, який не пов'язаний з їх власною енергетикою[1].
Інформація завжди пов'язана із матеріальним об'єктом (наприклад, папером, магнітною стрічкою тощо) або фізичним процесом (наприклад, електричним струмом, звуковою або електромагнітною хвилею тощо), які є її носіями. Інформація пов'язується з носієм через змінювання його певної властивості. Змінювання властивості матеріального об'єкта або фізичного процесу називається сигналом (слово сигнал утворене від англійського слова sign, що означає "знак"). Сигнал є способом відтворення інформації. Інформація отримується як реєстрація сигналу.
Вибір того чи іншого способу представлення інформації означає вибір певної мови. Мова програмування - знакова система для планування поведінки машини. Знакова система - сукупність узгоджень, які визначають набір знакових ситуацій. Знакова ситуація - первинне поняття семіотики, її елементами є знак та денотат. Знак - це позначення або ім'я, денотат - значення, зміст[2].
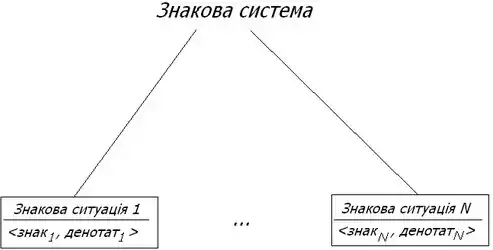
Основу будь-якої мови складає алфавіт - впорядкована сукупність усіх різних знаків мови. Кількість знаків, з яких складається алфавіт, іноді називають його потужністю.
У процесі передавання чи зберігання інформації часто доводиться переходити від одного способу подання інформації до іншого, тобто з однієї мови на іншу. Перетворення символів одного алфавіту на символи іншого алфавіту за певними правилами називається кодуванням, а результат цього перетворення - кодом[3].
Алгоритм задає машині точну інструкцію про виконання у певному порядку декотрої системи операцій, які дозволяють вирішити сукупність задач певного класу. Будь-який алгоритм подає процес розв'язування задачі як послідовність відокремлених простих дій. Дії виконуюься почергово, одна за одною, в усталеному порядку. Ця властивість алгоритму називається дискретністю. Алгоритм приводить від початкових даних до шуканого результату через скінченну кількість кроків (дій); при цьому дані варіюються у відомих межах.
Найбільш "інваріантною" частиною для усіх існуючих у математиці уточнень поняття алгоритму є клас частково рекурсивних арифметичних функцій (під частково арифметичною функцією розуміється часткове відображення із скінченної декартової степені множини натуральних чисел з у )[4].
Багато різних алгоритмів розглядаються у алгебрі та теорії чисел, а також у інших математичних дисциплінах. Наприклад, найпростіші алгоритми - правила, за якими виконуються арифметичні дії, алгоритм Евкліда, алгоритм взяття квадратного кореня та алгоритм обчислення визначників n-го порядку, правило Саррюса - алгоритм для обчислення визначників 3-го порядку, алгоритм обчислення рангу матриць, алгоритм визначення числа дійсних коренів алгебричного рівняння - правило Штурма тощо.
Проектування алгоритму має ієрархічну структуру і розпочинається з вершини ієрархії.
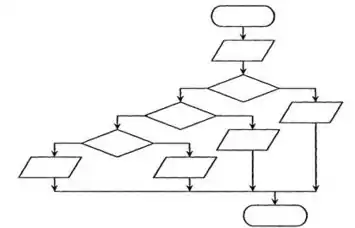
Таку структуру алгоритму називають також модульною, тому що кожна його підзадача становить собою модуль. Модуль - логічна частина алгоритму, яка є відносно незалежною, має певне цільове призначення і вирішує лише одну чітко сформульовану задачу.
Було доказано відсутність алгоритму для рішення ряду масових задач. Наприклад, академік П.С.Новіков доказав відсутність якого-небудь алгоритму для рішення проблеми тотожності у теорії груп.
Фізичні основи
На рівні частинок квантові системи описуються операторами, які належать декотрій алгебрі або супералгебрі Лі. Під квантуванням, починаючи з Н.Бора, розуміють деформацію з параметром деформації алгебри функцій (спостережуваних) на гладкому многовиді , наділеною дужкою Пуасона. Тобто квантування - це клас алгебр операторів параметризований параметром Причому для усіх значень параметра деформації , відмінних від нуля, це алгебра (самоспряжених) операторів, діючих у гільбертовому просторі а при ця алгебра збігається з алгеброю операторів множення на функції з початкової пуасонової алгебри функцій на задному многовиді яку називають алгеброю класичних спостережуваних, тобто При цьому, якщо на многовиді діяла група симетрій (пуасонівська група із пуасонівською дією), то ця дія зберігалася й на усіх алгебрах класу деформації
Нехай - векторний суперпростір розмірності над полем тобто такий -градуйований векторний простір, що Степінь елемента дорівнює (що записується ), якщо Супералгеброю є довільна -градуйована алгебра тобто така алгебра, що для усіх
Супералгебра над полем (зокрема, над полем комплексних чисел ) із добутком називається супералгеброю Лі, якщо цей добуток задовільняє аксіомам:
Добутком у супералгебрі Лі зазвичай називається дужка або суперкомутатор. Довільну асоціативну супералгебру (із добутком ) можна перетворити на алгебру Лі, якщо дужку задати формулою на односторонніх елементах й продовжити по лінійності на усю супералгебру.[5]
Розгляньмо модель із внутрішньою Лі-груповою динамікою на кристалічній ґратці, яка описується гамільтоніаном[6][7]:
де
де - спрощене позначення вузла кристалічної ґратки, - зовнішні поля, - взаємодія. Оператори характеризують різні властивості квантових систем і можуть бути операторами енергії певного рівня, спіновими операторами, операторами числа частинок, операторами електричного дипольного моменту тощо. Поля які відповідають цим операторам є величинами енергій, магнітних полів, хемічних потенціалів, електричних полів. Оператори задовільняють комутаційним співвідношенням
й визначають алгебру (супералгебру) Лі на вузлі Алгебра (супералгебра) Лі задає внутрішню Лі-групову динаміку квантової системи. Якщо є супералгеброю Лі, то дужка визначається співвідношенням
де коефіцієнт залежить від парності операторів
Твердотільна електроніка
У твердотільній мікроелектроніці розмір активної області приладів та пристроїв складає одиниці мікрон (1 мкм = м = ). Їхній енергетичний спектр з деяким ступенем точності можна вважати неперервним, оскільки відстань між сусідніми енергетичними рівнями (енергія розмірного квантування) має порядок де - характерний розмір області локалізації носіїв заряду, - їхня ефективна маса. Якщо вважати то
Тут - рідберґ, - борівський радіус. Таким чином, енергія розмірного квантування у таких пристроях набагато менша теплової енергії носіїв заряду за кімнатної температури (). Тому при описі фізичних явищ, пов'язаних із транспортом носіїв заряду у пристроях мікроелектроніки, таких, як діоди, транзистори, інтегральні мікросхеми тощо, можна обмежитися квазікласичним наближенням у фізиці твердого тіла.
На відміну від мікроелектроніки, у твердотільній наноелектроніці розмір активної області приладів та пристроїв складає декілька нанометрів (). Через таке просторове обмеження носіїв заряду у їх структурах енергія розмірного квантування має порядок Ця величина порівняна до ширини забороненої зони типових напівпровідників й на порядок перебільшує теплову енергію носіїв заряду за кімнатної температури. Відтак ефекти розмірного квантування будуть відігравати суттєву роль, визначаючи основні електрофізичні властивості напівпровідникових наноструктур.
Інструментом вивчення фізичних процесів, які відбуваються у пристроях наноелектроніки, є квантова механіка. Нині, в основному, пристрої та прилади базуються на напівпровідникових гетероструктурах. Провідність, теплопровідність та термоелектричні властивості матеріалів у зонній теорії пояснюються за допомогою розсіяння електронів на дефектах і коливаннях кристалічної ґратки (див. Ланцюг Тоди). Зонна теорія важлива для розуміння принципу дії різноманітних електронних пристроїв.
Вивчення ефекту електронного вітру сильно пов'язане із використанням напівпровідникових приладів, оскільки збільшення їх розмірів призводить до появи ефекту електронного вітру[8]. У зв'язку із цим у напівпровідникових пристроях починають виникати зони із аномальним опором, що іноді призводить до їх перегрівання й виходу з ладу.
Наносистемотехніка - сукупність методів моделювання, проектування й конструювання виробів різного функціонального призначення, у тому числі наноматеріалів, мікро- та наносистем із використанням квантоворозмірних, кооперативно-синергетичних, гігантських ефектів й інших явищ та процесів, які проявляються в умовах матеріальних об'єктів із нанометричними характеристичними розмірами[9][10].
Перспективним напрямком є магноніка та спінтроніка. Наприклад, щоб здійснити квантування спінових хвиль потрібно пов'язати компоненти магнітного моменту феромагнетику із операторами народження й поглинання спінових хвиль[11][12] (див. Спін).
Спеціальний захист. Чутливість мікросхем до локальних радіаційних ефектів характеризується величиною перетину ефекту (см2) - відношенням загальної кількості збоїв до флюенсу частинок, величиною порогових лінійних втрат енергіє йону (МеВ см2/мг), величиною порогової енергії протонів (МеВ), починаючи з якої спостерігається поява локальних радіаційних ефектів у інтегральних схемах.
Залежність перетину одиночних збоїв від порогових лінійних втрат енергії (для йонів) описується із використанням апроксимації функцією Вейбулла
де - перетин насичення, - параметри апроксимації, які не мають фізичного змісту.
З метою якісної оцінки ефективності застосування схемотехнічних методів підвищення стійкості до впливу окремих ядерних частинок обґрунтоване використання в якості характеристик стійкості параметрів, пов'язаних із фізичними характеристиками елементів: ефективний об'єм чутливої області елеента й критичний заряд, який лючислюється за формулою:
де - мінімальна величина перешкоди, яка викликає перемикання елемента, виражена у вольтах; - еквівалентна ємність елемента у пікофарадах. Величина критичного заряду може бути оцінена із схемотехнічних параметрів шляхом чисельного моделювання впливу імпульсу струму, імітуючого імпульс іонізованого струму, який виникає при збиранні заряду з треку частинки чутливою областю за рахунок дрейфових й дифузійних процесів.
Для КМОН підвищення стійкості полягає у рознесенні комірок, чутливих до впливів окремих ядерних частинок, а також взаємному включенні чутливих областей у простір суміжних комірок[13].
Квантовий канал зв'язку
Схема квантового каналу зв'язку зображена на наступному малюнку. Блок 1 позначає кодуючий пристрій, який перетворює сигнал , який потрібно передати у закодований сигнал Зворотне перетворення прийнятого закодованого сигналу у оцінювальний сигнал відбувається декодуючою ланкою 5. Блоки 1 та 5 можна вважати неквантовими й конструювати по відомим принципам неквантової теорії інформації.
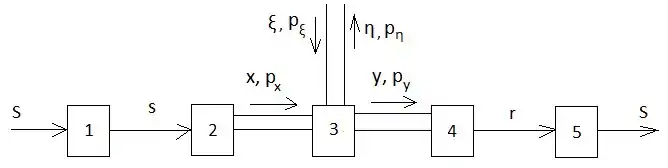
Ланки ж 2-4 є специфічними для квантових систем. Ланка 3 є власною лінією передачі, яка описується квантовими законами. У квантовій теорії, замість розподілу ймовірностей, характеристикою стану система є мариця щільності. Тому змінні на вході лінії зв'язку 3 писуються матрицею щільності Аналогічно змінні на виході лінії зв'язку (на прийомному кінці) описуються матрицею щільності Змінні а також є спряженими динамічними змінними (координата та імпульс, напруга та струм, електричне поле й магнітне поле), необхідними для повного опису квантової системи.
Ланка 2 на малюнку позначає пристрій, який за фіксованого сигналу виробляє відповідний йому стан змінних на передавальному кінці лінії зв'язку. Ланка 4 представляє собою зворотний пристрій. Він розташований на прийомному кінці лінії й перетворює змінні у вигідний сигнал Ця операція відповідає квантовомеханічній редукції (зміні декотрої фізичної змінної). В результаті цієї операції матриця щільності перетворюється на розподіл ймовірностей
У лінії 3 сигнал, пов'язаний із динамічними змінними змішується із шумом (шумові змінні позначені ), причому це змішування відбувається за квантовими законами[14]. Сигнал та шум є незалежними, оскільки породжуються у ланці 2, а породжуються у далеких від нього системах, пов'язаних із лінією 3. Сумісна матриця щільності дорівнює
Коли корисний сигнал дійде до прийомного кінця, пройде час і по законам квантової теорії зміна стану буде описуватися унітарним оператором
де - гамільтоніан системи. Якщо розглядати односторонній рух корисної хвилі уздовж лінії, то перетворення часу буде відповідати переходувід змінних , до змінних , де - змінні на прийомному кінці, а - декотрі інші (додаткові) змінні. Перетворення матриці щільності буде мати вигляд[15]
Оптичний канал зв'язку

Оптичний світловод — є фізичним середовищем транспортування оптичного сигналу і складається із серцевини та оболонки, що мають різні величини показників заломлення. Завдяки явищу повного внутрішнього відбиття, надається змога транспортувати оптичні сигнали (світло), що генеруються обладнанням, до якого підключене оптичне волокно. Квантові генератори є саме такими пристроями. Однією з важливих проблем фізики й квантової електроніки є генерація лазерного випромінювання у вигляді імпульсів якумога найменшої тривалості. Сучасні лазери здатні випромінювати імпульси тривалістю близько 5 фс, тобто менше двоїх періодів світлової хвилі, що є близьким до фундаментальної межі[16].
Оптичні солітони можуть розповсюджуватися у оптоволокні на значні відстані (декілька тисяч кілометрів) практично без спотворення форми й зберігатися при зіткненнях один із одним (тобто відновлювати напрямок руху, швидкість й амплітуду, демонструючи властивості, які є характерними для частинок)[17].
Логічні схеми
Кон'юнкція
Розгляньмо схему із перемикачами Логічним нулем на вході схеми будемо вважати розімкнений стан відповідного перемикача. Наприклад,
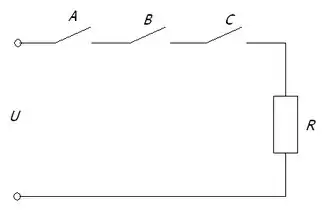
Логічний 0 на виході схеми () - такий її стан, коли через опір не пробігає струм. Таблиця істинності для даної логічної схеми має три входи - Кожна з цих логічних змінних може знаходитися у стані або логічного 0, або логічної 1. Відповідно, кількість комбінацій цих змінних дорівнює Є також очевидним те, що через опір перебігає струм тоді, коли замкнені одночасно усі перемикачі
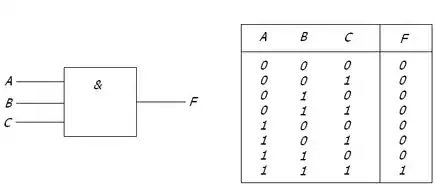
Таблиця істинності - таблиця, у якій містяться усеможливі комбінації вхідних логічних змінних й відповідні їм значення логічної функції. Відповідно, . Можна навіть так написати.
Правило логічного множення: якщо на вхід логічного елемента & подається хоча б один 0, то на його виході буде логічний 0.
Диз'юнкція
Таблиця істиності наступної логічної схеми складається з 4 рядків, оскільки схема має два входи - Кількість цих змінних дорівнює Через опір пробігає струм у тому випадку, коли замкнені або перемикач або перемикач Іншими словами, .
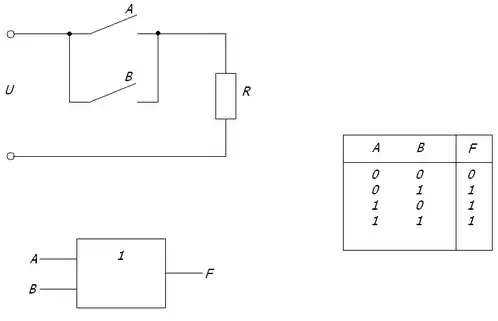
Правило логічного додавання: якщо на вхід елемента "АБО" подається хоча б одна логічна 1, на виході буде логічна 1.
Інверсія (логічне заперечення )
Таблиця істинності для наступної логічної схеми складається з двох рядків, оскільки ця схема має лише один вхід - Кількість варіантів для єдиної булевої змінної дорівнює Через опір пробігає струм тоді, коли перемикач не замкнений, тобто , у протилежному випадку
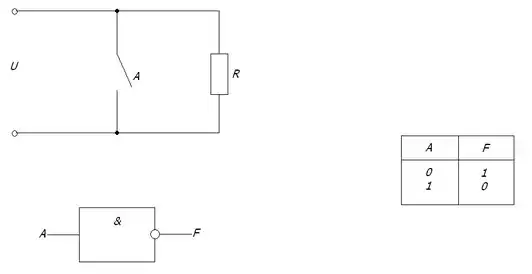
Правило інверсії: проходячи через інвертор, сигнал змінює значення на протилежне.
Кон'юнкція-Інверсія
Ця функція здійснює логічний добуток значень вхідних сигналів, а потім інвертує результат цього множення.
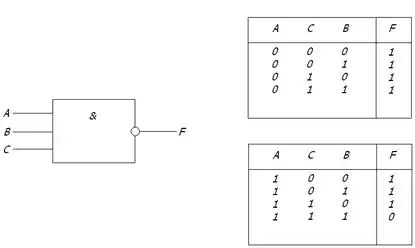
Правило: якщо на вхід логічного елемента "ТА-НІ" подається хоча б один логічний 0, то на виході буде логічна 1.
Диз'юнкція-Інверсія
Правило: якщо на вхід елемента "АБО-НЕ" подається хоча б одна логічна 1, то на виході буде логічний 0.
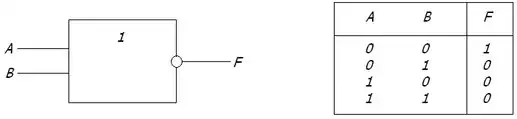
Карта Карно
Карта Карно - графічне представлення таблиці істинності. Кожній комірці карти Карно відповідає рядок таблиці істинності. По осям карти розкладаються комбінації змінних, а всередині карти - значення функції. Призначенням карти Карно є знаходження суми прямого та інверсного значення змінних.
Наприклад, для змінної така сума дорівнює при будь-якому значенні : при це буде при це Тому при винесенні за дужки у виразі
суму можна відкинути, при цьому результат виразу не змінитсься. У цьому і полягає мінімізація логічних виразів за допомогою карт Карно. Для досягнення цієї мети необхідно притримуватися правил розмітки осей карти:
- Вертикальна вісь розмічається незалежно від горизонтальної.
- Починати розмітку потрібно з будь-якої комбінації змінних.
- Усі комбінації змінних повинні бути перелічені.
- Для сусідніх комірок карти комбінації змінних повинні відрізнятися не більш ніж одним знаком, причому сусідніми є крайні клітинки рядка (стовпця).
Для функції двох змінних карта Карно - квадрат 2х2 клітини. У цих клітинах розміщуються 4 значення функції з останнього стовпця таблиці істинності.
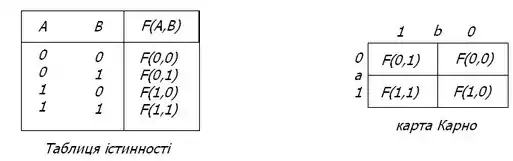
Для функції трьох змінних карта Карно - це прямокутник 2х4 або 4х2 клітини. Для функції п'яти змінних карта Карно - об'ємна фігура (куб 4х4х4 клітини).
Наприклад, складемо за схемою таблицю істинності.
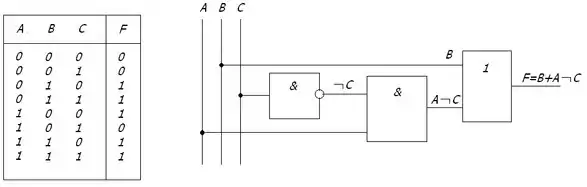
Замість значень логічної функції у загальному вигляді у комірки карти проставляються конкретні значення (логічні 0 та 1) з відповідних рядків таблиці істинності. Потім розглядаються лише ті комірки, які заповнені одиницями. Усі ці одиниці повинні бути обведені контурами по наступним правилам:
- Контури повинні бути прямокутними й містити кількість одиниць, яка дорівнює де - ціле число () Таким чином, у контурі може бути лише одна, або дві, або чотири, або вісім одиниць.
- Кількість одиниць у контурі повинне бути максимальним, при цьому контури можуть перетинатися між собою. Потрібно враховувати, що крайні рядки є сусідніми й крайні стовпці також є сусідніми, тому контури можуть бути розірваними.
- Кількість контурів повинна бути мінімальною, але усі одиниці повинні бути охоплені контурами. Не можна забувати про окремо стоячі одиниці. Кожна така одиниця - це контур, якому відповідає повний логічний добуток змінних.
При одному варіанті розмітки осей (ліворуч) перший контур, який складається з одиниць, виходить розірваним. Якщо ж прийняти розмітку, показану праворуч, то контур буде мати нормальні окреслення, а вираз, який йому відповідає, залишиться без змін.
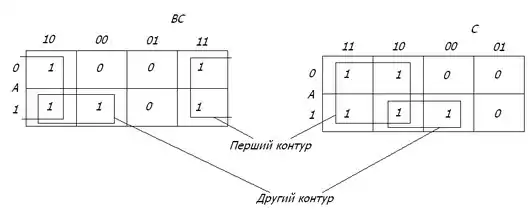
Перший контур охоплює чотири одиниці і йому відповідає сума мінітермів: у якій не змінюється лише змінна Другий контур охоплює усі одиниці. Йому відповідає сума мінітермів у якій змінна приймає обидва можливих значення, а добуток залишається незмінним. Таким чином, отримуємо мінімальний вираз:
Йому відповідає логічна схема, зображена на малюнку вище.
Рівносильні перетворення логічних схем
Комплекс - послідовність формул, для якої вказані кортежі (переліки) її вхідних величин та область задання. Комплекси є засобом формального опису операторів логічної схеми й застосовуються при рівносильних перетвореннях логічних схем. Формулою є вираз вигляду
(1)
де - декотра функція, а - її аргументи. Знак ":=" називається знаком присвоєння. Обчислення функції для конкретних значень її аргументів й присвоєння цього значення величині (яка раніше могла бути невизначеною або мати інше значення) називається виконанням формули (1).
Комплекс складається із вхідного кортежу декотрої послідовності формул виду (1), вихідного кортежу й -вимірної множини точок, координати яких є значеннями величин Можина повинна містити лише ті точки, відправляючись від значень, рівних координатам яких, можна послідовно виконати усі формули, які належать комплексу. Множина називається областю задання комплексу.
Застосування комплесу як зображення операторів логічної схеми пов'язане із тим, що, вважаючи буква назвами комірок запам'ятовуючого пристрою ЕОМ, можна перейти від формул комплексу до команд або групам команд програми[18].
Комплекси комплектуються у пакети комплексів - скінченну або зліченну множину комплексів, які мають однакові вхідні кортежі (переліки) й непересічні області задання.
Пам'ять
Адреса - величина, яка визначає місцеположення інформації у ЕОМ. Частіше за все адреса визначає номер комірки запам'ятовуючого пристрою, у якій зберігається одне машинне слово. Адресація - спосіб ідентифікації (розпізнавання) комірки пам'яті, регістра або іншого джерела даних.
Адресний простір - сукупність комірок, до яких можна звертатися при використанні фізичної адреси. Як правило, число таких комірок дорівнює де - число розрядів шини адреси.
Будь-яку цифрову ЕОМ можна розглядати як сукупність пам'яті й операційного пристрою. При описі ЕОМ під операційним пристроєм розуміють сукупність так званих операційних елементів, здійснюючих перетворення сигналів, а під пам'яттю машини - сукупність так званих комірок. При цьому комірками є не лише запам'ятовуючі елементи машин, але й канали зв'язку, по яким передаються сигнали від одних операційних елементів до інших. Пам'ять машини й її операційний пристрій пов'язані між собою таким чином, що на входи кожного операційного елемента сигнали надходять лише з комірок й з виходів операційних елементів передаються лише у комірки.
Елементарною коміркою, або розрядом, називають комірку, для якої існують два можливих стани: одне поставлене у взаємно однозначну відповідність 0, інше - 1. Обчислювальні машини містять елементи пам'яті із двома стійкими станами, які також можна позначати символами 0,1 (увімкнено-вимкнено або активний-неактивний). Спеціальний клас логічних схем, використовуваних у обчислювальних машинах, призначений для того, щоб по даним вхідним сигналам, які подаються на входів з елементів пам'яті у станах отримувати один або декілька функціонально визначених вихідних сигналів де функції явно вказані. Такі схеми називаються вентильними схемами або вентилями.
Нехай усяка комірка представляє собою послідовність розрядів, пронумерованих послідовно цілими числами. Усякий стан будь-якої комірки взаємно однозначно відповідає декотрому двійковому числу. Комірки можуть перетинатися між собою; наприклад, регістр команд ЕОМ сам є коміркою й містить у собі комірки (а значить перетинається з ними) для зберігання адрес команд й коду операції. Блоком комірок називають групу непересічних комірок. Окремі комірки (які не входять до блоків) й блоки комірок позначаються буквами тощо. Комірки, які входять до блоків, нумерують й позначають буквою (символ блоку) з індексом, який дорівнює номеру комірки у блоці (наприклад, - блок комірок, - комірка №25 цього блоку). Функціонування операційного пристрою машини складається з актів, кожний з яких полягає у тому, що по станам декотрої впорядкованої сукупності комірок визначається новий стан декотрої комірки Таким чином, кожний акт представляє собою виконання декотрого основного оператора над пам'яттю машини.
Найважливішими причинами накопичення помилок при обчисленнях є часте використання різниць (що призводить до втрати значащих цифр) й ділення на числа невідомого порядку величини (що призводить до переповнення розрядкої сітки). Цього варто запобігати за допомогою відповідної організації програми.
Машинний цикл - інтервал часу, протягом якого виконується одна машинна операція: вибірка команди, дешифрація її з метою аналізу й обчислення адрес операндів; звернення до пам'яті й зовнішніх пристроїв; виконання команди або її частин тощо. Машинний цикл складається з декількох машинних тактів.
Машинний такт - мінімальний робочий інтервал часу, протягом якого виконується одна елементарна дія. Тривалість машинного такту дорівнює періоду синхросигналу генератора тактових імпульсів.
Джерела
- Новосельцев. Теоретические основы системного анализа. с. 57.
- Теория и практика языков программирования. Учебник для вузов. 2-е изд.
- Великий довідник школяра: 5-11 класи. ISBN 966-8114-20-5.
- Ю.Л.Ершов - Теория нумераций.
- Стукопин Владимир Алексеевич - ЯНГИАНЫ СУПЕРАЛГЕБР ЛИ.
- Луцев Леонид Владимирович - Спиноволновые возбуждения и спинзависимые электротранспортные явления в наноразерных магнитных металл-диэлектрических гетероструктурах.
- L.V. Lutsev - DIAGRAM TECHNIQUE FOR QUANTUM MODELSWITH INTERNAL LIE-GROUP DYNAMICS.
- Электронный ветер в полупроводниках при резких перепадах температур // Физика и техника полупроводников. — 1986. _ Т. 20, вып. 10. — С. 1929—1931.
- В.В. Лучинин - Введение в индустрию наносистем.
- Афанасьев А.В,, Афанасьев В.П., Глинский Г.Ф., Голоудина С.И. и др. - Нанотехнология: физика, процессы, диагностика, приборы / Под ред. Лучинина В.В., Тинрова Ю.М.
- А.И.Ахиезер, В.Г.Барьяхтар, М.И.Каганов - Спиновые волны в ферромагнетиках и антиферромагнетиках. (Успехи физических наук, Т.LXXI, вып. 4, 1960 г.).
- А.М.Косович - Механіка кристалічної ґратки.
- Черкасов И.Г. - Субмикронные статические КМОП оперативные запоминающие устройства с повышенной сбоеустойчивостью к воздействию отдельных ядерных частиц.
- Б.А.Векленко, А.А.Рухадзе - О квантовой формуле Найквиста.
- . Л. Стратонович, Скорость передачи информа-ции в некоторых квантовых каналах связи,Пробл.передачи информ., 1966, том 2, выпуск 1, 45–57.
- П.Г.Крюков, Квантовая электроника, 2001, том 31, номер 2, 95-119.
- Портнов Эдуард Львович, Мариносян Эмиль Хачатурович - Классический солитон в телекоммуникациях и его основные параметры.
- А.И. Берг - Автоматизация производства и промышленная электроника. М.,1963. с. том 2.
