Лінійний оптичний квантовий комп'ютер

Вважається, що додавання нелінійності до лінійної оптичної мережі було достатнім для здійснення ефективних квантових обчислень.[12] Їх робота стала відомою як «схема KLM» або «протокол KLM», яка використовує лінійні оптичні елементи, джерела одиночних фотонів та детектори фотонів як ресурси для побудови квантової схеми обчислень, що включає лише допоміжні біти, квантову телепортацію та виправлення помилок. Він використовує інший спосіб ефективного квантового обчислення з лінійними оптичними системами та сприяє нелінійним операціям виключно з лінійними оптичними елементами.[3]

В основі своєї схеми KLM індукується ефективна взаємодія між фотонами шляхом проведення проективних вимірювань з фотоприймачами, що входить до категорії недетермінованих квантових обчислень. Він заснований на нелінійному зсуві знаків між двома кубітами, який використовує два допоміжні фотони та постселекцію.[13] Вона також базується на демонстрації того, що ймовірність успішної роботи квантових вентилів може бути наближена до одиниці за допомогою використання заплутаних станів, підготовлених недетерміновано, та квантової телепортації з однокубітовими операціями.[14][15] У іншому випадку без достатньо високого показника успіху одного квантового блоку вентилів може знадобитися експоненціальна кількість обчислювальних ресурсів. Тим часом схема KLM базується на тому, що належне квантове кодування може зменшити ресурси для отримання точно закодованих кубітів щодо досягнутої точності, а також може зробити ЛОКК стійким до відмов для втрати фотонів, неефективності детектора та декогеренції фази. Як результат, ЛОКК може бути надійно реалізований за допомогою схеми KLM з достатньо низькою вимогою до ресурсів, щоб запропонувати практичну масштабованість, роблячи її такою ж перспективною технологією для квантової обробки інформації, як і інші відомі реалізації.

Більш обмежена модель бозонного семплінгу була запропонована та проаналізована Ааронсоном та Архіповим у 2013 році.[16] Вона не вважається універсальною,[16] але все ще може вирішувати проблеми, які, як вважається, перевищують можливості класичних комп'ютерів, такі як проблема бозонного семплінгу. 3 грудня 2020 року команда на чолі з китайськими фізиками Пан Цзяньвей (潘建伟) та Лу Чаоян (陆朝阳) з Університету науки і техніки Китаю в Хефей, провінція Аньхой представила свої результати науці, в якій вони вирішила проблему, яка практично не піддається жодному класичному комп'ютеру; тим самим доводячи квантову перевагу їх заснованого на фотонах квантового комп'ютера під назвою Квантовий комп'ютер Джиу Джанг(九章量子计算机).[17] Проблема бозонного семплінгу була вирішена за 200 сдекунд, за їх підрахунками, для вирішення суперкомп'ютеру Sunway TaihuLight Китаю знадобиться 2,5 мільярда років — квантова перевага близько 10¹⁴. Джиу Джанг був названий на честь найстарішого збереженого математичного тексту Китаю Математика в дев'яти книгах (Jiǔ zhāng suàn shù).[18]

Кубіт — одна з основних одиниць квантової обробки інформації. Стан кубіта, який може бути представлений як ${\displaystyle \alpha |0\rangle +\beta |1\rangle }$ — це стан суперпозиції, який, якщо його буде виміряно в ортонормальному базисі ${\displaystyle \{|0\rangle ,|1\rangle \}}$, має ймовірність ${\displaystyle |\alpha |^{2}}$ потрапити в ${\displaystyle |0\rangle }$ стан та ймовірність ${\displaystyle |\beta |^{2}}$ перебування у стані ${\displaystyle |1\rangle }$, де ${\displaystyle |\alpha |^{2}+|\beta |^{2}=1}$ — умова нормалізації. Оптична мода — це розрізнений оптичний канал зв'язку, який, як правило, позначається індексами квантового стану. Існує багато способів визначити розрізнені оптичні канали зв'язку. Наприклад, набір мод може бути розрізнятися за поляризацією фотонів , яку можна виділити за допомогою лінійних оптичних елементів, різними частотами, або комбінацією двох наведених вище випадків.

Поляризаційні кубіти описуються через стан поляризації (горизонтальної ${\displaystyle H}$ та вертикальної ${\displaystyle V}$). Стан описується як ${\displaystyle \alpha _{0}|H\rangle +\alpha _{1}|V\rangle }$. Маніпуляції з ними здійснюються за допомогою поляризуючих дільників променя (які пропускають або відбивають фотон відповідно до його поляризації), поляризаторів, хвильових пластинок.[21]

Просторові кубіти використовують наявність одиничного фотона на одному з різних шляхів у просторі a та b. Стан описується як ${\displaystyle \alpha _{0}|a\rangle +\alpha _{1}|b\rangle }$. Може бути створений коли один фотон проходить через дільник променя з 2 виходами. Маніпуляції з ними здійснюються за допомогою дільників променя та фазоперетворювачів. Недоліком є те, що когерентність між ${\displaystyle |a\rangle }$ та ${\displaystyle |b\rangle }$ сильно залежить від відносного зсуву фаз між шляхами a та b, що важко проконтролювати на великих відстанях.[21]

Часові кубіти мають обчислювальний базис, що складається з двох станів однакової спектральної ширини, але зсунутих у часі більш ніж на час когерентності. Стійкі при передачі квантової інформації на великі відстані. Можуть бути реалізовані при проходженні одиничного фотона через незбалансований інтерферометр Маха–Цендера. Стан описується як ${\displaystyle \alpha _{0}|E\rangle +\alpha _{1}|L\rangle }$, де E означає раннє прибуття, а L означає пізнє прибуття.[21]

Можливі також інші кубіти, наприклад частотні.[21]

У протоколі KLM кожен з фотонів зазвичай знаходиться в одній з двох мод, і моди різняться між фотонами (можливість того, що мода зайнята більше, ніж одним фотоном, дорівнює нулю). Це не так лише під час реалізацій керованих квантових вентилів, таких як CNOT. Коли стан системи є таким, як описано, фотони можна розрізнити, оскільки вони перебувають у різних модах, і тому стан кубіта можна представити, використовуючи один фотон у двох модах, вертикальній (V) та горизонтальній (H): для Наприклад, ${\displaystyle |0\rangle \equiv |0,1\rangle _{VH}}$ і ${\displaystyle |1\rangle \equiv |1,0\rangle _{VH}}$. Загальноприйнятими є посилання на стани, визначені через зайняття мод, як стани Фока.

При бозонному семплінгу фотони не розрізняються, і тому не можуть безпосередньо представляти стан кубіта. Натомість представляється стан кудіта (квантового стану з d рівнів) всієї квантової системи, використовуючи стани Фока мод ${\displaystyle M}$, які зайняті ${\displaystyle N}$ нерозрізненими поодинокими фотонами (це ${\displaystyle {\tbinom {M+N-1}{M}}}$ -рівнева квантова система).

Щоб підготувати бажаний багатофотонний квантовий стан для ЛОКК, потрібен однофотонний стан. Тому буде використано нелінійні оптичні елементи, наприклад однофотонні генератори та деякі оптичні модулі. Наприклад, спонтанне параметричне розсіяння можна використовувати для умовного генерування стану ${\displaystyle |1\rangle \equiv |1,0\rangle _{VH}}$ у моді вертикальної поляризації в момент часу ${\displaystyle t}$ (індекси ігноруються для цього випадку одного кубіта). При використанні джерела одиничних фотонів, вихідний стан гарантується, хоча для цього може знадобитися кілька спроб (залежно від рівня успішності). Подібним чином можна підготувати спільний мульти-кубітовий стан. Взагалі, довільний квантовий стан може бути сформований для квантової обробки інформації за допомогою належного набору джерел фотонів.

Для досягнення універсальних квантових обчислень ЛОКК повинен мати можливість реалізувати повний набір універсальних вентилів. Цього можна досягти в протоколі KLM, але не в моделі бозонного семплінгу.

Ігноруючи виправлення помилок та інші проблеми, основним принципом реалізації елементарних квантових вентилів, що використовують лише дзеркала, дільники променів і фазоперетворювачі, є те, що за допомогою цих лінійних оптичних елементів можна побудувати будь-яку довільну 1-кубітну унітарну операцію; іншими словами, ці лінійні оптичні елементи підтримують повний набір операторів на будь-якому окремому кубіті.

Унітарна матриця, пов'язана з дільником променя ${\displaystyle \mathbf {B} _{\theta ,\phi }}$ :

${\displaystyle U(\mathbf {B} _{\theta ,\phi })={\begin{bmatrix}\cos \theta &-e^{i\phi }\sin \theta \\e^{-i\phi }\sin \theta &\cos \theta \end{bmatrix}}}$,

де ${\displaystyle \theta }$ та ${\displaystyle \phi }$ визначаються коефіцієнтом відбиття ${\displaystyle r}$ та коефіцієнтом проходження ${\displaystyle t}$. Для симетричного дільника променя, який має фазовий зсув ${\displaystyle \phi ={\frac {\pi }{2}}}$ за умови унітарності перетворення ${\displaystyle |t|^{2}+|r|^{2}=1}$ та ${\displaystyle t^{*}r+tr^{*}=0}$, може бути показано, що

${\displaystyle U(\mathbf {B} _{\theta ,\phi ={\frac {\pi }{2}}})={\begin{bmatrix}t&r\\r&t\end{bmatrix}}={\begin{bmatrix}\cos \theta &-i\sin \theta \\-i\sin \theta &\cos \theta \end{bmatrix}}=\cos \theta {\hat {I}}-i\sin \theta {\hat {\sigma }}_{x}=e^{-i\theta {\hat {\sigma }}_{x}}}$,

що являє собою обертання одиночного кубітового стану навколо осі x на кут ${\displaystyle 2\theta =2\cos ^{-1}(|t|)}$ у сфері Блоха.

Дзеркало — це особливий випадок, коли коефіцієнт відбиття дорівнює 1, так що відповідний унітарний оператор є матрицею обертання, заданою

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$.

Для більшості випадків дзеркал, що використовуються в квантовій обробці інформації, кут падіння ${\displaystyle \theta =45^{\circ }}$.

Аналогічно, оператор фазообертача ${\displaystyle \mathbf {P} _{\phi }}$ асоціюється з унітарним оператором, описаним ${\displaystyle U(\mathbf {P} _{\phi })=e^{i\phi }}$, або, якщо написано у 2-модовому форматі

${\displaystyle U(\mathbf {P} _{\phi })={\begin{bmatrix}e^{i\phi }&0\\0&1\end{bmatrix}}={\begin{bmatrix}e^{i\phi /2}&0\\0&e^{-i\phi /2}\end{bmatrix}}{\text{(глобальна фаза ігнорується)}}=e^{i{\frac {\phi }{2}}{\hat {\sigma }}_{z}}}$,

що еквівалентно обертанню на ${\displaystyle -\phi }$ відносно осі ${\displaystyle z}$.

Оскільки будь-які два ${\displaystyle SU(2)}$ обертання вздовж ортогональних обертових осей можуть генерувати довільні обертання в сфері Блоха, можна використовувати набір симетричних дільників променів і дзеркал для реалізації довільних операторів ${\displaystyle SU(2)}$ для квантової обробки інформації. На малюнках нижче наведено приклади реалізації вентиля Адамара та вентиля Паулі-X (вентиль НЕ) за допомогою дільників променя (зображені у вигляді прямокутників, що з'єднують два набори ліній перетину з параметрами ${\displaystyle \theta }$ і ${\displaystyle \phi }$) та дзеркал (зображено у вигляді прямокутників, що з'єднують два набори ліній перетину з параметром ${\displaystyle R(\theta )}$).

Реалізація вентиля Адамара за допомогою дільника променя та дзеркала. Квантова схема наверху.

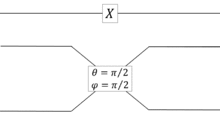Реалізація вентиля НЕ за допомогою дільника променя. Квантова схема наверху.

На наведених рисунках кубіт кодується за допомогою двох каналів мод (горизонтальних ліній): ${\displaystyle \left\vert 0\right\rangle }$ представляє фотон у верхній моді, а ${\displaystyle \left\vert 1\right\rangle }$ представляє фотон у нижній моді.

Перевага протоколу KLM перед моделлю бозонного семплінгу полягає в тому, що, хоча протокол KLM є універсальною моделлю, а бозонний семплінг не вважається універсальною моделлю. З іншого боку, здається, що проблеми масштабованості у бозонному семплінгу є більш керованими, ніж у протоколі KLM.

У бозонному семплінгу допускається лише одне вимірювання, вимірювання всіх мод в кінці обчислення. Єдина проблема масштабованості в цій моделі виникає внаслідок вимоги, щоб усі фотони надходили до детекторів фотонів протягом досить короткого інтервалу часу і з досить близькими частотами.[16]

У протоколі KLM існують недетерміновані квантові вентилі, які є важливими для того, щоб модель була універсальною. Вони покладаються на телепортацію вентилів, де безліч імовірнісних вентилів готуються в автономному режимі, а додаткові вимірювання проводяться в середині кола. Ці два фактори є причиною додаткових проблем із масштабованістю в протоколі KLM.

У протоколі KLM бажаним початковим станом є такий, при якому кожен з фотонів перебуває в одній з двох мод, і можливість того, що мода зайнята більш ніж одним фотоном, дорівнює нулю. Однак при бозонному семплінгу бажаний початковий стан є специфічним, що вимагає, щоб перші ${\displaystyle N}$ мод були зайняті одним фотоном[16] (${\displaystyle N}$- кількість фотонів і ${\displaystyle M\geq N}$ — кількість мод), а всі інші стани порожні.

Інша, більш рання модель, яка спирається на представлення кількох кубітів одним фотоном, заснована на роботах Ч. Адамі та Н. Дж. Серфа.[1]

Використовуючи як розташування, так і поляризацію фотонів, один і той же фотон у цій моделі може представляти кілька кубітів; однак, як результат, вентиль CNOT може бути реалізований лише між двома кубітами, представленими одним фотоном.

На малюнках нижче наведено приклади створення еквівалентних вентиля Адамара та вентиля CNOT за допомогою дільників променя (зображено у вигляді прямокутників, що з'єднують два набори ліній перетину з параметрами ${\displaystyle \theta }$ та ${\displaystyle \phi }$) і фазообертачами (зображені у вигляді прямокутників на лінії з параметром ${\displaystyle \phi }$).

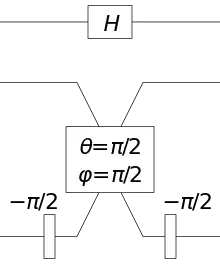Реалізація вентиля Адамара на кубіті «розташування» з дільником променя і фазообертачами. Квантова схема знаходиться у верхній частині.

Реалізація вентиля CNOT на з дільником променя. Квантова схема знаходиться у верхній частині.

У оптичній реалізації вентиля CNOT поляризація та розташування є контрольним та цільовим кубітом відповідно.