Напівнеперервна функція

Нехай ${\displaystyle X}$ — топологічний простір, ${\displaystyle x_{0}\in X}$ і ${\displaystyle f:X\to \mathbb {R} \cup \{-\infty ,\infty \}}$ функція зі значеннями у множині розширених дійсних чисел.

Функція ${\displaystyle f}$ називається неперервною зверху (знизу) в точці ${\displaystyle x_{0}}$ якщо для довільного ${\displaystyle \varepsilon >0}$ існує окіл ${\displaystyle U}$ точки ${\displaystyle x_{0}}$ такий, що ${\displaystyle f(x)\leqslant f(x_{0})+\varepsilon ,\;\forall x\in U\quad \left(f(x)\geqslant f(x_{0})-\varepsilon ,\;\forall x\in U\right),}$ якщо${\displaystyle f(x_{0})>-\infty \quad (f(x_{0})<\infty )}$, і ${\displaystyle f(x)}$ прямує до ${\displaystyle -\infty \quad (\infty )}$ коли ${\displaystyle x}$ прямує до ${\displaystyle x_{0}}$ якщо ${\displaystyle f(x_{0})=-\infty \quad (\infty )}$.

У випадку метричного простору ${\displaystyle (X,\varrho )}$ ці умови можна записати так

${\displaystyle \varlimsup _{x\to x_{0}}f(x)\leqslant f(x_{0})\;\left(\varliminf _{x\to x_{0}}f(x)\geqslant f(x_{0})\right),}$

де ${\displaystyle \varlimsup }$ позначає точну верхню границю.

Функція ${\displaystyle f}$ називається напівнеперервною зверху (знизу) на ${\displaystyle M\subset X}$, якщо вона є напівнеперервною зверху (знизу) для всіх ${\displaystyle x_{0}\in M}$.

Альтернативно функція є напівнеперервною зверху (знизу) на ${\displaystyle X}$ якщо ${\displaystyle \forall \alpha \in \mathbb {R} }$ множина ${\displaystyle \{x\in X:~f(x)<\alpha \}\quad (\{x\in X:~f(x)>\alpha \})}$ є відкритою. Ввівши в множині дійсних чисел топологію ${\displaystyle O_{<}:={\Big \{}\left[-\infty ,a\right);a\in \mathbb {R} \cup \{-\infty ,+\infty \}{\Big \}}}$ для топологічного простору ${\displaystyle (X,O)}$ маємо, що функція ${\displaystyle f\colon X\to \mathbb {R} }$ є напівнеперервною зверху, тоді і тільки тоді коли вона є неперервною в новій топології дійсних чисел: ${\displaystyle (X,O)\to (\mathbb {R} ,O_{<})}$. Для подібного визначення неперервності знизу для дійсних чисел слід ввести топологію ${\displaystyle O_{>}:={\Big \{}\left(a,\infty \right];a\in \mathbb {R} \cup \{-\infty ,+\infty \}{\Big \}}.}$ Дані означення можна узагальнити на довільну лінійно впорядковану множину з подібним визначенням топології.

• Ціла частина числа ${\displaystyle x\mapsto [x]}$ є напівнеперервною зверху функцією;
• Дробова частина числа ${\displaystyle x\mapsto \{x\}}$ напівнеперервна знизу.
• Функція Діріхле ${\displaystyle f(x)=\left\{{\begin{matrix}1&x\in \mathbb {Q} \\0&x\in \mathbb {R} -\mathbb {Q} \end{matrix}}\right.}$ є напівнеперервною зверху в усіх раціональних точках і напівнеперервною знизу в ірраціональних.
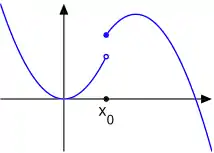
• Функція :${\displaystyle f(x)={\begin{cases}\sin(1/x)&{\mbox{if }}x\neq 0,\\1&{\mbox{if }}x=0,\end{cases}}}$

є напівнеперервною взверху в точці x = 0.

• Індикатор ${\displaystyle \mathbf {1} _{U}}$ довільної відкритої множини ${\displaystyle U\subset X}$ є напівнеперервною знизу функцією.
• Індикатор ${\displaystyle \mathbf {1} _{V}}$ довільної замкнутої множини ${\displaystyle V\subset X}$ є напівнеперервною зверху функцією.
• Нехай ${\displaystyle y'=F(x,y)\,,\quad y_{0}=y(x_{0})}$ — система звичайних диференціальних рівнянь (y — вектор порядку n). Нехай функція F визначена на множині ${\displaystyle E\subset \mathbb {R} ^{n+1}}$ і для кожної точки ${\displaystyle (x_{0},y_{0})\in E}$ існує єдиний максимальний розв'язок системи рівнянь ${\displaystyle y(x)}$, визначений на проміжку ${\displaystyle w_{-}<x<w_{+}.}$ Числа ${\displaystyle w_{-},w_{+}}$ загалом залежать від початкових умов і можна визначити функції ${\displaystyle w_{-}(x_{0},y_{0}),w_{+}(x_{0},y_{0})\;(x_{0},y_{0})\in E.}$ Тоді функція ${\displaystyle w_{-}(x_{0},y_{0})}$ є напівнеперервною зверху на множині E, а функція ${\displaystyle w_{+}(x_{0},y_{0})}$ є напівнеперервною знизу на множині E[1].

• Функція є неперервною тоді й лише тоді коли вона є одночасно напівнеперервною зверху і знизу.
• Якщо ${\displaystyle f\colon X\to \mathbb {R} }$ є напівнеперервною зверху, то функція -f є напівнеперервною знизу і навпаки.
• Нехай ${\displaystyle f,g:X\to \mathbb {R} }$ є дві напівнеперервні знизу (зверху) функції. Тоді їх сума ${\displaystyle f+g}$ також напівнеперервна знизу (зверху). Якщо напівнеперервні зверху функції є невідємними в точці то їх добуток теж буде напівнеперервним зверху.
• Якщо ${\displaystyle f,g}$ — напівнеперервні зверху функції дійсної змінної і g також неспадна, то функція ${\displaystyle f\circ g}$ є також напівнеперервною зверху.
• Межа монотонно зростаючої (спадної) послідовності напівнеперервних знизу (зверху) в точці ${\displaystyle x_{0}}$ функцій є напівнеперервною знизу (зверху) функцією в ${\displaystyle x_{0}}$. Більш точно, нехай дано послідовність напівнеперервних знизу (зверху) функцій ${\displaystyle f_{n}:X\to \mathbb {R} ,\;n\in \mathbb {N} }$ таких, що ${\displaystyle f_{n+1}(x)\geqslant (\leqslant )f_{n}(x)\;\forall n\in \mathbb {N} \;\forall x\in X.}$ Тоді якщо існує межа ${\displaystyle \lim \limits _{n\to \infty }f_{n}(x)=f(x)\;\forall x\in X,}$ то ${\displaystyle f}$ напівнеперервна знизу (зверху).
• Якщо ${\displaystyle u:X\to \mathbb {R} }$ і ${\displaystyle v:X\to \mathbb {R} }$ є напівнеперервні функції відповідно знизу і зверху , і на всьому просторі виконано

${\displaystyle -\infty <v(x)\leqslant u(x)<\infty ,\;x\in X,}$

то існує неперервна функція ${\displaystyle f:X\to \mathbb {R} }$, така що

${\displaystyle v(x)\leqslant f(x)\leqslant u(x),\;x\in X.}$

• Нехай дано компактну множину ${\displaystyle K\subset X.}$ Тоді напівнеперервна знизу (зверху) функція ${\displaystyle f:K\to \mathbb {R} }$ досягає на ${\displaystyle K}$ свого мінімуму (максимуму).
• Теорема Віталі — Каратеодорі. Якщо ${\displaystyle \mu }$ — невід'ємні міра на ${\displaystyle \mathbb {R} ^{n}}$, то для будь-якої ${\displaystyle \mu }$-вимірної функції ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ існують дві послідовності функцій ${\displaystyle \{u_{k}\}_{k=1}^{\infty }}$ і ${\displaystyle \{v_{k}\}_{k=1}^{\infty }}$, що задовольняють умовам:

1. ${\displaystyle u_{k}}$ — напівнеперервні знизу, ${\displaystyle v_{k}}$ — напівнеперервні зверху,
2. кожна функція ${\displaystyle u_{k}}$ є обмеженою знизу, кожна функція ${\displaystyle v_{k}}$ — зверху,
3. послідовність ${\displaystyle u_{k}}$ незростаюча, послідовність ${\displaystyle v_{k}}$ неспадна,
4. ${\displaystyle v(x)\leqslant f(x)\leqslant u(x),\;x\in \mathbb {R} ^{n},}$
5. ${\displaystyle \lim \limits _{n\to \infty }u_{n}(x)=\lim \limits _{n\to \infty }v_{n}(x)=f(x),\;\;}$ ${\displaystyle \mu }$-майже всюди.
6. якщо для ${\displaystyle E\subset \mathbb {R} ^{n}}$ функція ${\displaystyle f}$ є інтегровною за Лебегом на ${\displaystyle E}$ (${\displaystyle f\in L(E)}$), то також ${\displaystyle u_{k},v_{k}\in L(E)}$ і

${\displaystyle \lim \limits _{n\to \infty }\int _{E}u_{n}d\mu =\lim \limits _{n\to \infty }\int _{E}v_{n}(x)d\mu =\int _{E}f(x)d\mu .}$

• Перестюк М. О., Станжицький О. М., Капустян О. В., Ловейкін Ю. В. Варіаційне числення та методи оптимізації: Навч. посібник. — К., 2010. — 121 c.
• Gaal, Steven A.(2009), Point set topology, New York: Dover Publications, ISBN 978-0-486-47222-5 (англ.)