Ірраціональні числа

Ірраціональні числа (позначення для множини — $\mathbb {I}$ ) — це всі дійсні числа, що не є раціональними: $\mathbb {I} =\mathbb {R} \setminus \mathbb {Q}$ , — тобто не можуть бути записані як відношення цілих чисел ${\frac {z}{n}}$ ( $z\in \mathbb {Z}$ , $n\in \mathbb {N}$ ), а лише нескінченними неперіодичними десятковими дробами.

Математична константа пі (π) є ірраціональним числом.

Число

\scriptstyle {\sqrt {2}}

є ірраціональним числом.

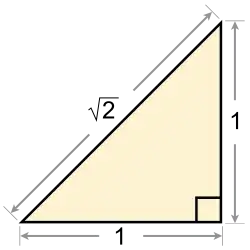
Уперше І. ч. постали в геометрії під час вивчення довжин відрізків піфагорцями, які, як стверджує легенда^{[джерело?]}, виявили неспівмірність з одиницями вимірювання деяких геометричних величин. Оскільки це суперечило їхній філософії (цілком побудованій на натуральних числах), відкриття якнайсуворіше приховували, навіть покаравши на смерть одного зі своїх братів — Гіппаса Метапонтського, який (за різними джерелами) чи то першим знайшов, чи то розголосив цей факт.

Відмінності записування дійсних чисел

Десятковий дріб будь-якого раціонального числа має періодично повторювану частину (зокрема це можуть бути нулі, як у скінченних дробів і цілих чисел), н-д:

${\frac {1}{3}}={}.{\overline {3}}$ ,[1] що означає «нуль цілих і три в періоді» (довжина періоду — один), тобто $3$ повторюється нескінчену кількість разів;
${\frac {22}{7}}=3.{\overline {142857}}$ , що означає «три цілих і сто сорок дві тисячі вісімсот п'ятдесят сім у періоді» (довжина періоду — шість), тобто $142857$ повторюється нескінчену кількість разів;
${\frac {265}{132}}=2.00{\overline {75}}$ , що означає «дві цілих, нуль сотих і сімдесят п'ять у періоді» (довжина періоду — два), тобто $75$ повторюється нескінчену кількість разів;
${\frac {5}{2}}=2.5\equiv 2.5{\overline {0}}$ , скінченний дріб «дві цілих, п'ять десятих»,[2] тобто $0$ повторюється нескінчену кількість разів;
${\frac {3}{1}}=3.{}\equiv 2.{\overline {9}}$ , ціле число «три еквівалентне двом цілим і дев'ять у періоді»,[3] тобто $9$ повторюється нескінчену кількість разів.

Періодичність дробу можна вважати критерієм приналежності числа до множини раціональних чисел.

Розкладання І. ч. у десятковий дріб не позначається такою періодичністю. Наприклад, відомо, що число пі — ірраціональне та навіть трансцендентне, тому, хоча в його десятковому записі окремі цифри та їх комбінації повторюються, не існує групи цифр, яка б нескінченно повторювалася, утворюючи період.

Інший спосіб записування додатних дійсних чисел: за допомогою ланцюгових дробів. Відмінність полягає в тому, що ланцюгові дроби раціональних чисел скінченні, а І. ч. — нескінченні, хоча для квадратичних ірраціональностей ланцюговий дріб періодичний.

Квадратні корені

Квадратний корінь з двох — це перше число, ірраціональність якого було доведено. Іншим відомим ірраціональним числом є золотий перетин. Квадратні корені усіх натуральних чисел, які не є квадратними числами, є ірраціональними.

Приклади

{\frac {355}{113}}=3+{\cfrac {1}{7+{\cfrac {1}{16}}}},

— скінченний;

{\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ldots }}}}}}=[1;2,2,2\ldots ]=[1;(2)]

— з періодом довжини один;

{\sqrt {3}}=1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+\ldots }}}}}}}}=[1;1,2,1,2\ldots ]=[1;(1,2)]

— з періодом довжини два;

\pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+\ldots }}}}}}}}=[3;7,15,1,292,1,1,1,2,\ldots ]

(A001203 в енциклопедії цілих послідовностей) — неперіодичний.

Філософське значення

Про існування неспівмірних відрізків знали вже древні математики: їм була відома, наприклад, неспівмірність діагоналі та сторони квадрата, що рівносильно ірраціональності числа ${\sqrt {2}}$ (перше знайдене І. ч.).

Піфагорове твердження, що всі речі є числа, відображало метафізичні уявлення стародавніх греків про Всесвіт як місце гармонії, яку власне можна описати відношеннями натуральних чисел. Так поєднання двох звуків, відношення частот яких є раціональним числом, дає приємне для вуха звучання.

З'ясування того, що ${\sqrt {2}}\approx 1{,}4142135$ не є раціональним числом, призвело до глибокої кризи давньогрецької математики, яка полягала в усвідомлені факту існування математичних величин, які не можливо відобразити числами, а лише через геометричні побудови. Як наслідок — давньогрецька математика відмовилася від алгебраїчного підходу, на користь геометричного.

Властивості

Будь-яке дійсне число можна записати нескінченним десятковим дробом, проте тільки І. ч. записують неперіодичними десятковими дробами.
Сума двох додатних І. ч. може бути раціональним числом.
Кожне І. ч. визначає такий переріз Дедекінда у множині раціональних чисел $\mathbb {Q}$ , для якого в нижньому класі немає найбільшого, а у верхньому — найменшого числа.
Кожне І. ч. є або алгебраїчним, або трансцендентним. Кожне дійсне трансцендентне — ірраціональним.
Множина І. ч. скрізь щільна на числовій прямій, тобто між будь-якими двома дійсними числами є І. ч. (і навіть нескінченно багато).
Порядок на множині І. ч. — ізоморфний порядку на множині дійсних трансцендентних чисел.
Множина І. ч. є незліченною, другої категорії.

Топологічні властивості $\mathbb {R} \setminus \mathbb {Q}$

є підпростором евклідового простору $\mathbb {R}$ ;
є G_δ-множиною, але не F_σ-множиною в $\mathbb {R}$ , фактично: $\mathbb {R} \setminus \mathbb {Q} =\bigcap _{\alpha \in \mathbb {Q} }(\mathbb {R} \setminus \{\alpha \})$ ;
є метричним простором, цілком нормальним і паракомпактним;
є повним простором другої категорії;
є сепарабельним простором;
задовольняє другу аксіому зліченності;
не є локально-компактним і σ-локально-компактним;
є цілком відокремленим;
є щільним у собі;
не є розсіяним;
є нульвимірним.

Див. також

Міра ірраціональності

Примітки

Тут використано англійську систему записування дробів без нулів. У пострадянських країнах для розділення цілої частини від дробної використовують кому замість крапки, а для позначення повторюваної частини — дужки замість верхньої риски.
Десяткові дроби є нескінченними за побудовою, тому зрозуміло, що після певного десяткового знаку можуть стояти самі нулі ( $a_{0},a_{1}...a_{n}000...$ ), відкиданням яких отримують скінченні дроби.
Можемо записати як нескінченний періодичний дріб, оскільки з означення маємо, що $2+{\frac {9}{10}}+{\frac {9}{100}}+...=3$ .

Література

1.Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (вид. Dover reprint of 1978). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 507446.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Тут використано англійську систему записування дробів без нулів. У пострадянських країнах для розділення цілої частини від дробної використовують кому замість крапки, а для позначення повторюваної частини — дужки замість верхньої риски.

[2] Десяткові дроби є нескінченними за побудовою, тому зрозуміло, що після певного десяткового знаку можуть стояти самі нулі ( $a_{0},a_{1}...a_{n}000...$ ), відкиданням яких отримують скінченні дроби.

[3] Можемо записати як нескінченний періодичний дріб, оскільки з означення маємо, що $2+{\frac {9}{10}}+{\frac {9}{100}}+...=3$ .