Основна теорема про лишки

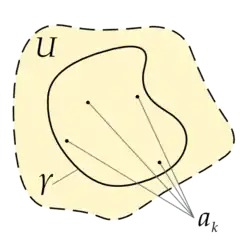
Нехай U — відкрита, однозв'язна підмножина комплексної площини ${\displaystyle \mathbb {C} }$, z₁,...,z_n множина особливих точок у U і f — функція що є голоморфною у множині U - {z₁,...,z_n}. Якщо γ — деяка замкнута спрямлювана крива у U, якій не належать z_k. Тоді  :

${\displaystyle \oint _{\gamma }f(z){\text{d}}z=2\pi i\sum _{k=1}^{n}\operatorname {Res} (f,z_{k})\,\mathrm {Ind} _{\gamma }(z_{k}).}$

В даній рівності, Res(f,z_k) позначає лишок функції f в точці z_k, а ${\displaystyle \mathrm {Ind} _{\gamma }(z_{k})}$ індекс контуру γ відносно точки z_k.

Дане число може бути визначене за формулою:

${\displaystyle \operatorname {Ind} _{\gamma }(z_{k})={\frac {1}{2\pi i}}\int _{\gamma }{\frac {{\text{d}}z}{z-z_{k}}}.}$

Замітка. У найпоширенішому випадку крива вважається жордановою, тобто вона ніде не перетинається сама з собою. В такому випадку крива розбиває область U на дві частини внутрішню та зовнішню. Для внутрішніх особливих точок (як на малюнку) в таких випадках ${\displaystyle \mathrm {Ind} _{\gamma }(z_{k})=1}$, для зовнішніх ${\displaystyle \mathrm {Ind} _{\gamma }(z_{k})=0}$ і їх можна не враховувати. Тоді рівність із твердження теореми перепишеться:

${\displaystyle \oint _{\gamma }f(z){\text{d}}z=2\pi i\sum _{k=1}^{n}\operatorname {Res} (f,z_{k})}$

де сума береться по всіх внутрішніх особливих точках.

Нехай F — множина особливих точок функції f, і для ${\displaystyle z_{0}\in F}$, функція допускає розклад у ряд Лорана в деякому проколотому диску ${\displaystyle D(z_{0},r)\backslash \{z_{0}\}}$ радіуса ${\displaystyle r>0}$ з центром у точці ${\displaystyle z_{0}}$ :

${\displaystyle f(z)=\sum _{n\in \mathbb {Z} }b_{z_{0},n}(z-z_{0})^{n}}$

Нехай ${\displaystyle h_{z_{0}}}$ ряд, визначений із сингулярної частини ряду Лорана :

${\displaystyle h_{z_{0}}(z)=\sum _{-\infty }^{-1}b_{z_{0},n}(z-z_{0})^{n}}$

Він є нормально збіжним на компактних підмножинах ${\displaystyle U-\{z_{0}\}}$ .

Визначимо функцію g у всій множині U як:

${\displaystyle g(z)=f(z)-\sum _{z_{i}\in F}h_{z_{i}}(z)}$

Дана функція є голоморфною в усій області U і тому згідно з інтегральною теоремою Коші:

${\displaystyle \oint _{\gamma }g(z)dz=0}$

згідно з визначенням функції g :

${\displaystyle \oint _{\gamma }f(z)dz=\sum _{z_{i}\in F}\oint _{\gamma }h_{z_{i}}(z)dz}$

Зважаючи на нормальну збіжність ${\displaystyle h_{z_{i}}}$ можна записати :

${\displaystyle \oint _{\gamma }h_{z_{i}}(z)dz=\sum _{-\infty }^{-1}b_{z_{i},n}\oint _{\gamma }(z-z_{i})^{n}dz}$

Обчислюючи інтеграли одержуємо :

${\displaystyle \oint _{\gamma }(z-z_{i})^{n}dz={\begin{cases}2i\pi \mathrm {Ind} _{\gamma }(z_{i})&n=-1\\0&n\neq -1\end{cases}}}$

Об'єднавши дві попередні формули можна одержати:

${\displaystyle \oint _{\gamma }f(z)dz=2i\pi \sum _{z_{i}\in F}b_{z_{i},-1}\mathrm {Ind} _{\gamma }(z_{i})}$

і згадавши визначення лишка одержуємо необхідний результат:

${\displaystyle \oint _{\gamma }f(z)dz=2i\pi \sum _{z_{i}\in F}\mathrm {Res} (f,z_{i})\mathrm {Ind} _{\gamma }(z_{i})}$

• Лишок
• Інтегральна формула Коші
• Інтегральна теорема Коші
• Принцип аргументу

• Residue theorem на сайті MathWorld
• Residue Theorem Module by John H. Mathews
• Приклади застосування

• Дьедонне Ж. Основы современного анализа, — М. Мир, 1964
• Шабат Б. В. Введение в комплексный анализ. — М.: Наука. — 1969, 577 стр.
• Mitronivić, Dragoslav; Kečkić, Jovan (1984), The Cauchy method of residues: Theory and applications, D. Reidel Publishing Company, ISBN 90-277-1623-4
• Rudin, Walter, Real and Complex Analysis, McGraw-Hill, ISBN 978-0070542341
• Zill Dennis G., Shanahan Patrick D., A first course in complex analysis with applications, Jones and Bartlett Publishers, Inc., ISBN 0763714372