Проєктивна модель

Проєктивна модель (модель Кляйна, модель Бельтрамі — Кляйна) — модель геометрії Лобачевского, запропонована італійським математиком Еудженіо Бельтрамі. Німецький математик Фелікс Кляйн розробив її незалежно.

Через точку проходить нескінченно багато прямих, що не перетинають пряму

За її допомогою доводиться несуперечливість геометрії Лобачевського в припущенні несуперечливості евклідової геометрії.

Історія

Цю модель запропонував Бельтрамі, поряд з моделлю Пуанкаре і моделлю псевдосфери[1]

Ще раніше, 1859 року цю модель побудував Кейлі. Але він розглядав її лише як деяку конструкцію в проєктивній геометрії і, мабуть, не помітив зв'язку її з неевклідовою геометрією. 1869 року з його роботою ознайомився 20-річний Кляйн. Він згадує, що 1870 року виступив з доповіддю про роботи Кейлі на семінарі Веєрштрасса і, як він пише, «закінчив її питанням, чи не існує зв'язку між ідеями Кейлі і Лобачевського. Я отримав відповідь, що це — дві дуже віддалені за ідеєю системи». Як каже Кляйн «я дозволив переконати себе цими запереченнями і відклав убік вже дозрілу думку». Однак 1871 року він до цієї думки повернувся, оформив її математично і опублікував[2].

Модель

Площину Лобачевського подано в цій моделі відкритим диском, обмеженим деяким колом — абсолютом. Точки абсолюту, так звані «ідеальні точки», площині Лобачевського вже не належать. Пряма площини Лобачевського — це хорда абсолюту, що з'єднує дві ідеальні точки.

Рухами геометрії Лобачевського в проєктивній моделі оголошуються проєктивні перетворення площини, що переводять внутрішність абсолюту в себе. Конгруентними вважаються фігури всередині абсолюту, що переводяться одна в одну такими рухами. Якщо точки і лежать на хорді так, що порядок їх проходження на прямій , тоді відстань у площині Лобачевського визначається як

де позначає подвійне відношення,  — радіус кривини площини Лобачевського.

Зауваження
  • Будь-який факт евклідової геометрії, описаний такою мовою, подає деякий факт геометрії Лобачевського. Іншими словами, будь-яке твердження неевклідової геометрії Лобачевського на площині є не що інше, як твердження евклідової геометрії на площині, що стосується фігур усередині кола, переказане в зазначених термінах.
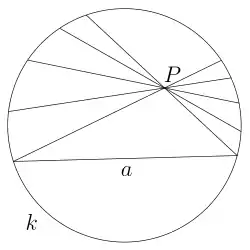
  • Евклідова аксіома про паралельні явно не виконується в цій моделі, оскільки через точку , що не лежить на даній хорді , проходить скільки завгодно хорд, що не перетинають її.

Властивість
  • Дві хорди перпендикулярні, якщо, продовжені за межі диска, кожна проходить через полюс іншої (полюс хорди — це точка перетину дотичних до абсолюту в кінцевих точках хорди). Хорди, що проходять через центр диска, мають полюс на нескінченності, ортогональний до напрямку хорди (звідси випливає, що прямі кути на діаметрах не спотворені).
  • Кола в моделі стають еліпсами;
  • Орициклам відповідають еліпси, що мають з абсолютом дотик порядку 4.
  • Еквідистанті прямої відповідають дуги еліпсів, дотичних до абсолюту в двох абсолютних точках цієї прямої.

Див. також

Примітки
  1. Eugenio Beltrami, Teoria fondamentale degli spazii di curvatura costante, Annali. di Mat., ser II, 2 (1868), 232—255.
  2. Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, гл. XII, пар. 2, — Физматлит, Москва, 2009.

Література
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.