Розподіл Леві
В теорії ймовірностей і математичній статистиці, розподіл Леві — неперервний розподіл ймовірностей для невід'ємної випадкової величини, названий на честь французького математика Поля Леві.
| Леві | |
|---|---|
 | |
|
Функція розподілу ймовірностей 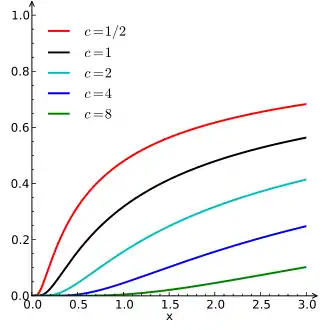 | |
| Параметри | ; |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | , for |
| Мода | , for |
| Дисперсія | |
| Коефіцієнт асиметрії | undefined |
| Коефіцієнт ексцесу | undefined |
| Ентропія |
де — Стала Ейлера—Маскероні |
| Твірна функція моментів (mgf) | невизначена |
| Характеристична функція | |
Цей розподіл є одним з кількох стійких розподілів, густина імовірності яких може бути записана аналітично. Іншими прикладами є нормальний розподіл і розподіл Коші.
Визначення
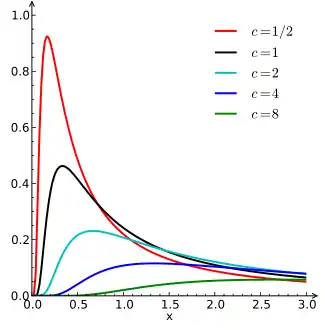
Густина імовірності розподілу Леві на множині визначається
де — параметр розміщення, — коефіцієнт масштабування. Функція розподілу ймовірностей:
де — доповнююча функція помилок. Параметр зміщує криву вправо на відстань , змінюючи носій функції на множину [, ). Як усі стійкі розподіли, розподіл Леві має стандартну форму f(x;0,1) з властивістю:
де y визначено як
Характеристична функція розподілу Леві визначається формулою:
Для , the nth момент незміщеного розподілу Леві формально визначаються:
Проте для всіх значень n > 0 інтеграл у формулі розбігається і моменти для розподілу є невизначеними. Твірна функція моментів формально визначається:
і розбігається для і, відповідно, теж не є визначеною.
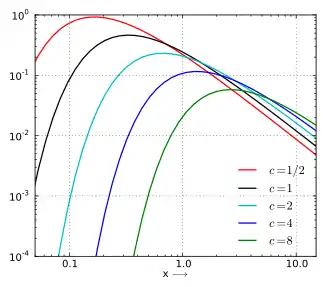
Як і всі стійкі розподіли окрім нормального, для розподілу Леві характерний «важкий хвіст». Хвіст функції густини розподілу асимптотично поводиться як степенева функція:
Це легко побачити на графіку де функції густини для різних значень c при показані в логарифмічному масштабі:
Пов'язані розподіли
- Якщо тоді
- Якщо тоді (обернений гамма-розподіл)
- Розподіл Леві є частковим випадком розподілу Пірсона типу 5.
- Якщо (нормальний розподіл) тоді
- Якщо тоді
- Якщо тоді (Стійкий розподіл)
- Якщо тоді (Масштабований обернений розподіл хі-квадрат)
Див. також
Посилання
- Information on stable distributions. Архів оригіналу за 22 липня 2013. Процитовано July 6 2012. Особливо An introduction to stable distributions, Chapter 1