Алгебрична теорія графів

Алгебрична теорія графів — напрямок у теорії графів, що застосовує алгебричні методи до теоретико-графових задач (на додачу до геометричного, комбінаторного та алгоритмічного напрямків). У свою чергу, алгебрична теорія графів поділяється на три гілки: лінійно-алгебричну[⇨], теоретико-групову[⇨] і вивчає інваріанти графів[⇨].

Граф Келі для знакозмінної групи A4, утворює зрізаний тетраедр у тривимірному просторі. Всі графи Келі вершинно-транзитивні, але деякі вершинно-транзитивні графи (наприклад, граф Петерсена) не є графами Келі.
Високосиметричний граф Петерсена, який є вершинно-транзитивним, симетричним, дистанційно-транзитивним і дистанційно-регулярним. Діаметр графу дорівнює 2. Група автоморфізмів графу містить 120 елементів і, фактично, є симетричною групою .

Лінійна алгебра

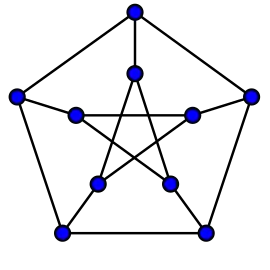
Характерний представник лінійно-алгебричної гілки — спектральна теорія графів, у якій вивчають спектри матриці суміжності або матриці Кірхгофа графу. Для графу Петерсена, наприклад, спектр матриці суміжності дорівнює (-2, -2, -2, -2, 1, 1, 1, 1, 1, 3). Деякі теореми пов'язують властивості спектра з іншими інваріантами графу. Простий приклад: зв'язний граф з діаметром матиме щонайменше різних значень у своєму спектрі[1]. Властивості спектра графу використовують для аналізу синхронізованості мереж.

Правильне розфарбування вершин графу Петерсена трьома кольорами, мінімально можливим числом кольорів. З хроматичного многочлена випливає, що існує 120 таких розмальовок у 3 кольори.

Теорія груп

У теорико-груповій гілці використовують методи загальної алгебри та алгебричної комбінаторики, а також геометричну теорію груп; одна з основних досліджуваних конструкцій — автоморфізми графів (утворюють групу). Увага приділяється різним сімействам графів, заснованих на симетрії (такі як симетричні графи, вершинно-транзитивні графи, реберно-транзитивні графи, дистанційно-транзитивні графи, дистанційно-регулярні графи і сильно регулярні графи), та зв'язків між цими сімействами. Деякі з цих категорій містять мале число графів, так що їх можна перерахувати. За теоремою Фрухта всі групи можна подати як групи автоморфізмів зв'язних графів (більше того, кубічних графів)[2]. Інший зв'язок з теорією груп — якщо задано будь-яку групу, можна утворити графи, відомі як графи Келі, і вони мають властивості, пов'язані зі структурою графу[1].

Групова гілка тісно пов'язана з лінійно-алгебричною, оскільки властивості симетрії графу відбиваються в його спектрі. Зокрема, спектр графу з високою симетрією, такого як граф Петерсена, має мало різних власних значень[1] (у графу Петерсена 3 значення, що є найменшим можливим числом для графу з таким діаметром, як у графу Петерсена). Для графів Келі спектр може бути пов'язаний прямо зі структурою групи, зокрема, з її незвідними представленнями[1][3].

Інваріанти графів

Алгебричні властивості інваріантів графів, таких, як хроматичні многочлени, многочлени Татта, інваріанти вузлів, дозволяють вивчати структуру графів алгебричними засобами. Наприклад, хроматичний многочлен графу, підраховує число його правильних розмальовок вершин; для графу Петерсена цей многочлен дорівнює:

[1],

зокрема, це означає, що граф Петерсена можна розфарбувати правильно одним або двома кольорами, але трьома кольорами його можна розфарбувати 120 різними способами. Багато робіт у цій галузі пов'язано зі спробами довести теорему про чотири фарби. Залишається багато відкритих питань, пов'язаних з інваріантами, наприклад, таких, як визначення графів, що мають той самий хроматичний многочлен, і визначення, які многочлени є хроматичними.

Примітки
  1. Biggs, 1993.
  2. Frucht, 1949.
  3. Babai, 1996.

Література
  • R. Frucht. Graphs of Degree 3 with given abstract group // Canad. J. Math.. — 1949. — Вип. 3 (21 січня).
  • Norman Biggs. Algebraic Graph Theory. — 2nd. — Cambridge : Cambridge University Press, 1993. — ISBN 0-521-45897-8.
  • L Babai. Handbook of Combinatorics / R Graham, M Grötschel, L Lovász. — Elsevier, 1996.
  • Chris Godsil, Gordon Royle. Algebraic Graph Theory. — New York : Springer-Verlag, 2001. — Т. 207. — (Graduate Texts in Mathematics)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.