Брамагупта
| Брамагупта | |
|---|---|
| санскр. ब्रह्मगुप्त | |
 | |
| Народився |
598 Бхілман, Індія |
| Помер | 668 |
| Місце проживання | Бхілман, тепер у штаті Раджастхан, Індія[1] і Удджайн, тепер у штаті Мадх'я-Прадеш, Індія |
| Країна | Індія |
| Діяльність | математик, астроном |
| Галузь | математика, астрономія |
| Відомий завдяки: | «Перегляд системи Брами» |
Брамагу́пта (санскр. ब्रह्मगुप्त; 598 — 668) — давньоіндійський математик і астроном, який написав важливі роботи з математики та астрономії а саме: теоретичний трактат «Brāhmasphuṭasiddhānta» («Брахма-спхута-сіддханта», може перекладатись як «Удосконалене вчення Брахми» чи «Перегляд системи Брами»), завершений у 628-му році, та більш практичний текст «Khaṇḍakhādyaka» («Кхандакхадьяка»), який побачив світ у 665-му[2]. Трактати написані у віршованій формі, що було досить популярним явищем серед індійських математиків. Ці роботи справили значний вплив на розвиток астрономії у Візантії та ісламських країнах, поклавши початок використанню алгебраїчних методів для астрономічних обчислень.
Біографічні дані
Вважається, що Брамагупта народився у 598 році. Це випливає з книги «Брахма-спхута-сіддханта», у якій він повідомляє, що написав цей текст у тридцятирічному віці у 628 році (Śaka 550)[3][4]. Брамагупта народився у Бхілламалі (тепер місто Бхілман у штаті Раджастхан Північно-Західної Індії). У стародавні часи місто Бхілман було резиденцією влади Ґуджар. Його батьком був Джиснугупта[5]. Він, ймовірно, прожив більшу частину свого життя в Бхілмані під час правління (і, можливо, під патронажем) короля Вяжрамукха[6], тому його нерідко називають Бхілламакарья (вчитель з Бхіллама)[7]. Брамагупта керував астрономічною обсерваторією в Удджайні. Обсерваторія, у якій також працював Варахаміхіра, була найкращою у тогочасній Індії[5].
Під час свого перебування в Бхілмані написав чотири твори з математики та астрономії. У 628 р. виклав четверту індуїстську астрономічну систему у віршованій формі у творі «Перегляд системи Брами» (Брахма-спхута-сіддханта). Дві його глави присвячені математиці, в тому числі арифметичній прогресії, доведенню різних геометричних теорем і розв'язанню квадратних рівнянь, які мають дійсні розв'язки. Решта 23 глави присвячені астрономії: у них описані фази Місяця, з'єднання планет, дані розрахунки щодо положень планет. Велика частина роботи присвячена затемненням Сонця і Місяця, розрахунку розташування планет в гороскопі.
До нас дійшов лише твір Брамагупти «Перегляд системи Брахми» (628), значна частина якого присвячена арифметиці й алгебрі. У ньому викладено відомості про арифметичну прогресію (правило знаходження суми), методи розв'язування квадратних рівнянь з дійсними коренями, а також розв'язування в цілих числах деяких неозначених квадратних рівнянь виду ax²+c=y², метод розв'язування неозначених лінійних рівнянь виду ax+c=by з використанням методу послідовних дробів[5][8].
Внесок у математику
Уведення поняття нуля
В своїй праці «Брахма-спхута-сіддханта» Брамагупта дав означення нуля як результату віднімання з числа самого числа. Він одним з перших встановив правила арифметичних операцій над додатними і від'ємними числами та нулем, розглядаючи при цьому додатні числа як майно, а від'ємні числа як борг. Далі Брамагупта намагався розширити арифметику давши означення ділення на нуль. Згідно з Брамагуптою[5]:
- Ділення нуля на нуль є нулем;
- Ділення додатного або від'ємного числа на нуль є дробом з нулем у знаменнику;
- Ділення нуля на додатне або від'ємне число дає нуль.
Тотожність Брамагупти
Тотожність Брамагупти стверджує, що добуток двох сум двох квадратів саме є сумою двох квадратів, причому двояким чином.
Наприклад,
Геометрія
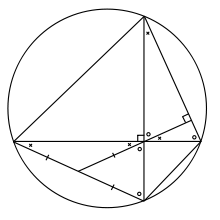
Теорема Брамагупти
Нехай є вписаний чотирикутник, діагоналі якого взаємно перпендикулярні. Опустимо з точки перетину діагоналей перпендикуляр на одну з його сторін. Якщо продовжити його по інший бік від точки перетину діагоналей, цей перпендикуляр ділить протилежну сторону чотирикутника на дві рівні частини[9].
Формула Брамагупти
Формула Брамагупти є узагальненням формули Герона для площі трикутника на випадок чотирикутника, вписаного у коло. А саме, площа S вписаного у коло чотирикутника зі сторонами a, b, c, d і півпериметром p дорівнює
Відома ще одна формула Брамагупти для радіуса описаного кола довільного трикутника:
де a, b, c — сторони трикутника, , та — його висоти.
Задача Брамагупти
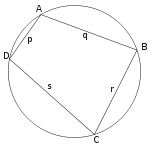
Задача Брамагупти — побудувати за допомогою циркуля та лінійки вписаний чотирикутник за чотирма його сторонами[10]. Одне з рішень використовує кола Аполлонія.
Розв'язування квадратних рівнянь
Одне з перших відомих виведень формули для знаходження коренів квадратного рівняння належить Брамагупті[11]. Він першим запропонував універсальне правило знаходження коренів рівняння, зведеного до канонічного вигляду . При цьому передбачалося, що в ньому усі коефіцієнти, крім можуть бути від'ємними. Сформульоване ученим правило за своєю суттю збігається із сучасним.
Інтерполяційна формула Брамагупти
У своїх наукових працях Брамагупта запропонував інтерполяційну формулу другого порядку, що є частковим випадком виведеної більше ніж через 1000 років по тому інтерполяційної формули Ньютона — Стірлінга. Він використовував її для інтерполяції значень синуса у складених ним тригонометричних таблицях[12]. Формула дає оцінку значення функції f при значенні її аргумента a + xh (при h > 0 та −1 ≤ x ≤ 1), коли її значення уже відоме у точках a − h, a та a + h. Вона записується так:
де Δ — оператор висхідної скінченної різниці першого порядку, тобто
Внесок в астрономію
Деякі дослідники вважають, що араби познайомилися з індійською астрономією у VIII столітті виключно завдяки праці Брамагупти Брахма-спхута-сіддханта.[13] Халіф Аль-Мансур (712—775) запросив 770 року до Багдаду вченого з Удджайна на ім'я Канків, який викладав індійську систему астрономії на основі Брахма-спхута-сіддханта. На прохання халіфа математик та філософ Мухаммед аль-Фазарі переклав праці Брамагупти на арабську мову.
Астрономічні подання Брамагупти, викладені в Брахма-спхута-сіддханта, свідчать про високий рівень його досліджень та наукової прозорливості. Так, у сьомому розділі праці, яка називається «Про затемнення Місяця», Брамагупта спростовує уявлення про те, що Місяць знаходиться далі від Землі, ніж Сонце.[14]
7.1. Якби Місяць був вище Сонця, то її ближня до Сонця половина завжди була б освітлена.7.2. Аналогічно, освітлену Сонцем частину Місяця завжди було б видно, а неосвітлена частина залишалася б невидимою.
7.3. Яскравість [освітленої частини Місяця] збільшується у напрямку до Сонця. Наприкінці світлого півмісяця ближча половина освітлена, а інша половина темна. Відтак, висоту рогів півмісяця можна обчислити.— Plofker, Kim (2007). "Mathematics in India". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
Брамагупта пояснює, що оскільки Місяць ближче до Землі, ніж Сонце, ступінь освітленості Місяця залежить від взаємного розташування Сонця та Місяця, і може бути обчислена виходячи з величини кута між цими двома небесними тілами.
Важливим внеском Брамагупти в астрономію є методи розрахунку положення небесних тіл з плином часу (ефемериди), їх сходів та заходів, з'єднань, а також розрахунку сонячних та місячних затемнень. Брамагупта піддав критиці уявлення пуранічної космології про те, що Земля є пласкою або порожнистою. Він стверджував що Земля і небо мають сферичну форму і що Земля рухається. 1030 року газневідський астроном Аль-Біруні у своїй праці «Та'ріх аль-Гінд», прокоментував роботу Брамагупти. Біруні зазначав, що на зауваження критиків теорії кулястої Землі («Якби це було так, то камені та дерева падали б з землі») Брамагупта відповів:
«Навпаки, якби це було не так, то Земля не могла б зберігати свою форму навіть протягом хвилин. […] Усі важкі речі притягуються до центру землі […] Земля однакова з усіх боків. Всі люди на Землі стоять, і всі важкі речі падають на землю за законом природи, так влаштована природа Землі, щоб притягувати та тримати речі, так як природа води — текти, вогню — горіти, вітру — приводити в рух… Земля — це єдина низька річ, всі предмети завжди повернуться до неї з будь-якого напрямку, куди б ви їх не кинули, і ніколи не піднімуться вгору від землі».— Брамагупта, Брахма-спхута-сіддханта (628) (cf. al-Biruni (1030), Indica)
Про силу тяжіння Землі Брамагупта говорив:
«Тіла падають на землю, оскільки це в природі Землі — притягувати їх, так само як в природі води-текти.»— Thomas Khoshy, Elementary Number Theory with Applications, Academic Press, 2002, p. 567. ISBN 0-12-421171-2.
Твори
«Брахма-спхута-сіддханта»
Основна праця Брамагупти, «Брахма-спхута-сіддханта» (628), містить 25 розділів:
- Про стан земної кулі і форму неба та землі.
- Про обертання світил і про визначення часу; про те, як знаходити середні положення світил; про визначення синуса дуги.
- Про складання таблиці світил.
- Про три проблеми, а саме: про тіні, про частину дня, що минула, і про гороскопи; а також про те, як виводити одне з них з іншого.
- Про те, як світила з'являються через промення Сонця і як вони ховаються за ними.
- Про те, як показується молодий місяць, і про його два роги.
- Про затемнення Місяця.
- Про затемнення Сонця.
- Про тіні Місяця.
- Про з'єднання та протистоянні світил.
- Про широти світил.
- Про критику того, що міститься у книгах та таблицях, і про розрізнення правильного від неправильного.
- Про арифметику та її застосування в обчисленні відстаней і в інших випадках.
- Про уточнення середнього положення світил.
- Про виправлення таблиці світил.
- Про точне дослідженні трьох проблем.
- Про відхилення затемнень.
- Про точне визначення появи молодого місяця і його двох рогів.
- Про метод «Куттак».
- Про розрахунки у розмірах віршів та метриці.
- Про кола та інструменти.
- Про чотири виміри часу — по Сонцю, по сходу, по Місяцю і по місячним станціям.
- Про знаки для чисел і цифр у віршованих творах з цього предмету.
- Про докази, що не використовують математику.
«Брахма-спхута-сіддханта» була перекладена арабською у 771 році математиком і філософом Ібрахімом аль-Фазарі. Переклад, який було виконано у вигляді таблиць — Зіджа — з необхідними поясненнями та рекомендаціями, отримав назву «Великий Сіндхінд». Відомо, що цією роботою користувався перський математик аль-Хорезмі (770—850) для написання своїх праць з астрономії («Зідж аль-Хорезмі») та арифметики («Книга про індійську арифметику»). Вважається, що переклад останньої у XI століття латинською відіграв вирішальну роль в поширенні позиційної системи числення[15][16].
«Брахма-спхута-сіддханта» була перекладена китайськими математиками VII—IX ст. (відомо принаймні чотири переклади), що дозволило поширити десяткову систему серед китайських вчених[2]. У 1817 році дві математичні глави були перекладені англійською Генрі Томасом Колбруком[7].
«Кхандакхадьяка»
Друга наукова праця Брамагупти, «Кхандакхадьяка» (665), також є фундаментальною працею з астрономії[17]. Вона містить 8 глав. У цій роботі Брамагупта уточнив й спростив низку методик астрономічних розрахунків, користуючись багато у чому системою, запропонованою Аріабхатою[18]. Крім цього, вона включає інтерполяційну формулу для обчислення синусів[5]. У VIII столітті «Кхандакхадьяка» була перекладена арабською під назвою «Арканд»[18].
Коментарі до Кхандакхадьяки були написані у 864, 966, 1040, 1180 роках, деякі з них не збереглись. Сама книга була надрукована в Калькутті у 1925 та 1941 роках. Переклад англійською зробив Сенгупта (англ. Prabodh Chandra Sengupta) у 1934 році[7].
Див. також
Примітки
- Sachau, Edward C. (2013). Alberuni's India. Routledge. с. 156. ISBN 978-1-136-38357-1.
- Pearce Ian. Brahmagupta, and the influence on Arabia. MacTutor History of Mathematics archive. Архів оригіналу за 15 вересня 2013. Процитовано 20 серпня 2013.
- Brahmagupta, Bhaskara, Henry-Thomas Colebrooke, 1817, с. xxxv-xxxvi.
- Brahmagupta. Encyclopedia of World Biography. 2006. Процитовано 20 серпня 2013.
- J J O'Connor and E F Robertson. Brahmagupta. MacTutor History of Mathematics archive. Архів оригіналу за 15 вересня 2013. Процитовано 20 серпня 2013.
- Plofker, 2007, с. 418—419.
- Brahmagupta. Complete Dictionary of Scientific Biography. Процитовано 20 серпня 2013.
- Plofker, 2007, с. 428—434.
- Michael John Bradley The Birth of Mathematics: Ancient Times to 1300. — Publisher Infobase Publishing, 2006. — P 70, 85. — ISBN 0816054231
- Прасолов В. В. Задачи по планиметрии, в 2-х ч. — М.: Наука, 1986.
- Энциклопедический словарь юного математика, 1985.
- Joseph, George G. (2000). [https://books.google.co.uk/books?id=c-xT0KNJp0cC The Crest of the Peacock]. Princeton, NJ: Princeton University Press. с. 285-286. ISBN 0-691-00659-8..
- Brahmagupta, and the influence on Arabia. Retrieved 23 December 2007.
- Plofker, Kim (2007). «Mathematics in India». The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
- Young, M. J. L.; Latham, J. D.; Serjeant, R. B. (2 листопада 2006). Religion, Learning and Science in the 'Abbasid Period. Cambridge University Press. с. 302–303. ISBN 978-0-521-02887-5.
- van Bladel, Kevin (28 листопада 2014). Eighth Century Indian Astronomy in the Two Cities of Peace. У Asad Q. Ahmed; Benham Sadeghi; Robert G. Hoyland. Islamic Cultures, Islamic Contexts: Essays in Honor of Professor Patricia Crone. BRILL. с. 257–294. ISBN 978-90-04-28171-4.
- Takao Hayashi. Brahmagupta. Британська енциклопедія. Архів оригіналу за 16 вересня 2013. Процитовано 20 серпня 2013.
- Katz V. J., Imhausen A. История человечества. — Издательский дом Магистр-Пресс, 2003. — Т. IV. VII-XVI века. — P. 410-412. (рос.)
Джерела
- Brahmagupta, Bhaskara, Colebrooke H.-T. Algebra, with arithmetic and mensuration, from Sanscrit of Brahmagupta and Bhascara. — John Murray, 1817. — 378 p. (англ.)
- Plofker K. Mathematics in India // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A sourcebook / Editor Katz V. J. — Princeton University Press, 2007. — 685 p. (англ.)
- Ван дер Варден Б. Л. Уравнение Пелля в математике греков и индийцев. / Успехи математических наук. — 1976. — Т. 31. — С. 57-70.
- Володарский А. И. Очерки истории средневековой индийской математики. — М. : Наука, 1977. — 187 с.
- Юшкевич А. П. История математики в средние века. — М. : Физматгиз, 1961.
- Gupta, Radha Charan (2008). Brahmagupta. У Selin, Helaine. Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (Springer): 162–163. ISBN 978-1-4020-4559-2, ISBN 1-4020-4425-9.
- O'Leary, De Lacy (2001) [first published 1948]. How Greek Science Passed to the Arabs (вид. 2nd). Goodword Books. ISBN 8187570245.
- Plofker, Kim (2007). Mathematics in India. The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
- Stillwell, John (2004). Mathematics and its History (вид. Second). Springer Science + Business Media Inc. ISBN 0-387-95336-1.
- Hockey, Thomas, ред. (2007). Brahmagupta. Biographical Encyclopedia of Astronomers. Springer Science & Business Media. с. 165. ISBN 0387304002.
- Bose, D. M.; Sen, S. N.; Subbarayappa, B. V. (1971). A Concise History of Science in India. New Delhi: Indian National Academy of Science. с. 95–97. Архів оригіналу за 8 грудня 2015. Процитовано 22 лютого 2019.
- Bhattacharyya, R. K. (2011). Brahmagupta: The Ancient Indian Mathematician. У B. S. Yadav; Man Mohan. Ancient Indian Leaps into Mathematics. Springer Science & Business Media. с. 185–192. ISBN 978-0-8176-4695-0.
- Boyer, Carl B. (1991). A History of Mathematics. John Wiley & Sons, Inc. ISBN 0-471-54397-7.
- Cooke, Roger (1997). The History of Mathematics: A Brief Course. Wiley-Interscience. ISBN 0-471-18082-3.
- Еремеева А. И., Цицин Ф. А. История астрономии (основные этапы развития астрономической картины мира). — М. : Изд. МГУ, 1989. — 349 с..
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М. : Педагогика, 1985. — С. 133-136.
Посилання
- Brahmagupta's Brahma-sphuta-siddhanta edited by Ram Swarup Sharma, Indian Institute of Astronomical and Sanskrit Research, 1966. English introduction, Sanskrit text, Sanskrit and Hindi commentaries (PDF)
- Algebra, with Arithmetic and mensuration, from the Sanscrit of Brahmegupta and Bháscara, translated by Henry Thomas Colebrooke.
- Brahmagupta Brahma-Sphuta-Siddhanta. - New Delhi, 1966.