Дзета-розподіл

zeta
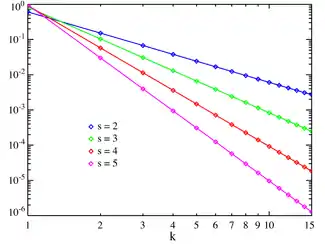	; Plot of the Zeta PMF on a log-log scale. (The function is only defined at integer values of k. The connecting lines do not indicate continuity.)
	Функція розподілу ймовірностей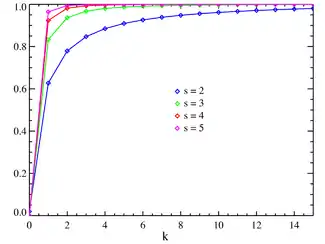
Параметри
Носій функції
Розподіл імовірностей
Функція розподілу ймовірностей (cdf)
Середнє
Мода
Дисперсія
Ентропія
Твірна функція моментів (mgf)	does not exist
Характеристична функція

У теорії ймовірності та статистиці дзета -розподіл є дискретним розподілом ймовірностей . Якщо X є дельта-розподіленою випадковою величиною з параметром s, то ймовірність того, що X прийме ціле значення k, задається наступною функцією ймовірності

f_{s}(k)=k^{-s}/\zeta (s)\,

де ζ ( s ) є дзета -функцією Рімана, яка є невизначена при s = 1.

Кратності окремих простих множників від X є незалежними випадковими величинами .

Дзета -функція Рімана, як сума всіх доданків $k^{-s}$ при цілому додатному числі k, виглядає як нормалізація розподілу Зипфа . Терміни "розподіл Зипфа" та "дзета -розподіл" часто використовуються як взаємозамінні. Але варто звернути увагу, що хоча розподіл дзети сам по собі є імовірнісним розподілом, він не асоціюється із законом Зіффа з тією самою експонентою.

Визначення

Зета -розподіл є визначений для натуральних чисел $k\geq 1$ , а її функція ймовірності задається як

P(x=k)={\frac {1}{\zeta (s)}}k^{-s}

,

де $s>1$ є параметром і $\zeta (s)$ - дзета-функція Рімана .

Кумулятивна функція розподілу задається формулою

P(x\leq k)={\frac {H_{k,s}}{\zeta (s)}},

де $H_{k,s}$ - узагальнене гармонічне число

H_{k,s}=\sum _{i=1}^{k}{\frac {1}{i^{s}}}.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.