Діагональний метод Кантора

У теорії множин, Діагональний метод Кантора або діагональний аргумент Кантора, також відомий як метод діагоналізації, був опублікований у 1891 році Георгом Кантором як математичний доказ того, що існують нескінченні множини для котрих не існує взаємно однозначної відповідності з нескінченною множиною натуральних чисел[1][2][3]. Такі множини тепер називають незліченними множинами, і розміри незліченних множин вивчає теорія кардинальних чисел, започаткована Кантором.

Ілюстрація діагонального аргументу  Кантора існування незліченних множин. Послідовність s не може входити у наведений перелік послідовностей.
Бієкція f(x) = 2x із натуральних у парні числа показує, що нескінченна множина може мати однакову потужність із точною підмножиною себе самої. Однак, діагональний метод Кантора показує, що  існують нескінченні множини різних потужностей.

Кантор вперше довів незліченність дійсних чисел у 1874 році іншим методом, відмінним від діагонального[4][5]. Однак діагональний метод є потужним і універсальним способом, що був відтоді використаний у широкому діапазоні доведень[6], включаючи першу теорему Геделя про неповноту і тезу Черча — Тюрінга. Аргументи діагоналізації також часто є джерелом суперечностей, таких як парадокс Рассела[7][8] і парадокс Рішара[9].

Незліченна множина

У статті 1891 року Кантор розглянув множину T усіх нескінченних послідовностей двійкових чисел (тобто кожна цифра числа є нулем або одиницею). Він почав із конструктивного доведення такої теореми:

Якщо s1, s2, … , sn, … є довільним переліком елементів із T, то завжди існує елемент s із T якому не відповідає жоден елемент sn у переліку.

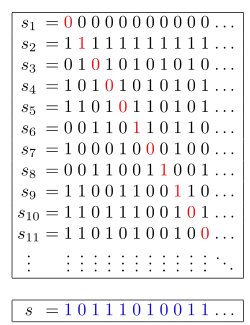
Доведення починається із перелічення усіх елементів із T, наприклад:

s1 = (0, 0, 0, 0, 0, 0, 0, ...)
s2 = (1, 1, 1, 1, 1, 1, 1, ...)
s3 = (0, 1, 0, 1, 0, 1, 0, ...)
s4 = (1, 0, 1, 0, 1, 0, 1, ...)
s5 = (1, 1, 0, 1, 0, 1, 1, ...)
s6 = (0, 0, 1, 1, 0, 1, 1, ...)
s7 = (1, 0, 0, 0, 1, 0, 0, ...)
...

Далі, послідовність s будується вибираючи 1-шу цифру оберненою до 1-ї цифри s1 (замінюючи 0 на 1 і навпаки), 2-гу цифру оберненою до 2-ї цифри s2, 3-тю цифру оберненою до 3-ї цифри s3, і загалом для кожного n, n-та цифра s є  оберненою до n-тої цифри sn. Для прикладу вище отримаємо:

s1 = (0, 0, 0, 0, 0, 0, 0, ...)
s2 = (1, 1, 1, 1, 1, 1, 1, ...)
s3 = (0, 1, 0, 1, 0, 1, 0, ...)
s4 = (1, 0, 1, 0, 1, 0, 1, ...)
s5 = (1, 1, 0, 1, 0, 1, 1, ...)
s6 = (0, 0, 1, 1, 0, 1, 1, ...)
s7 = (1, 0, 0, 0, 1, 0, 0, ...)
...
s = (1, 0, 1, 1, 1, 0, 1, ...)

За побудовою, s відрізняється від кожного sn, оскільки їхні n-ті цифри відрізняються (підсвічені у прикладі). Тому s не може бути у переліку.

На основі цієї теореми, використовуючи доведення від супротивного Кантор показує, що:

Множина T є незліченною.

Доведення починається із припущення, що T зліченна. Тоді всі її елементи можуть бути записані як перелік s1, s2, … , sn, … . Використання попередньої теореми до цього переліку дає елемент s, який не належить до переліку. Але, це суперечить тому, що s є елементом T і тому належить до переліку. Із суперечності випливає, що первісне припущення хибне. Отже, T незліченна.

Дійсні числа

Незліченність дійсних чисел вже була встановлена першим доведенням незліченності Кантора, але вона також випливає із попереднього результату. Для доведення цього будується ін'єкція f з множини T нескінченних двійкових рядків у множину R дійних чисел. Оскільки T є незліченною, то образ цієї функції f, який є підмножиною R, теж незліченний. Отже, множина R теж є незліченною. Також Кантор запропонував спосіб побудови бієкції між T і R. Отже, T і R мають однакову потужність, яка називається "потужністю континууму" і зазвичай позначається .

Ін'єкція з T у R визначається відображенням рядків із T у десяткові числа, наприклад t = 0111… у число 0.0111…. ця функція визначена як f(t) = 0.t, є ін'єкцією, оскільки відображає різні рядки у різні числа.

Узагальнення для множин

Кантор використав узагальнену форму діагонального аргументу щоби довести Теорему Кантора: для кожної множини S, булеан S — тобто, множина всіх підмножин S (позначена як P(S))—має більшу потужність ніж сама S. Доведення відбувається так:

Нехай f буде будь-якою функцією із S у P(S). досить довести, що f не може бути сюр'єкцією. Це значить що деякий елемент T із P(S), тобто деяка підмножина S, не лежить в образі f. Розглянемо таку множину:

T = { s ∈ S: s ∉ f(s) }.

Для кожного s із S, або s належить T або ні. Якщо s належить T, то за визначенням T, s не належить f(s), тобто T не дорівнює f(s). З іншої сторони, якщо s не належить T, то за визначенням T, s належить f(s), тобто знову T не дорівнює f(s).

Наслідки

Із цього випливає що поняття множини всіх множин є суперечливим. Якби S була множиною всіх множин, то P(S) була б одночасно більшою за S і підмножиною S.

Парадокс Рассела показав, що наївна теорія множин, що базується на аксіомній схемі необмеженого розуміння, є суперечливою. 

Діагональний метод показує, що множина дійсних чисел більша за множину натуральних (і разом цілих та раціональних). Отже, можна запитати чи існує множина потужність якої посередині між потужністю цілих і дійсних чисел. Це питання приводить до континуум-гіпотези. Аналогічно, питання чи існує множина з потужністю між  |S| і |P(S)| для деякої нескінченної S приводить до  узагальненої континуум-гіпотези.

Примітки
  1. Georg Cantor (1891). Ueber eine elementare Frage der Mannigfaltigkeitslehre. Jahresbericht der Deutschen Mathematiker-Vereinigung 1890—1891 1: 75–78. Англійський переклад: Ewald, William B. (ed.) (1996). From Immanuel Kant to David Hilbert: A Source Book in the Foundations of Mathematics, Volume 2. Oxford University Press. с. 920–922. ISBN 0-19-850536-1.
  2. Keith Simmons (30 липня 1993). Universality and the Liar: An Essay on Truth and the Diagonal Argument. Cambridge University Press. с. 20–. ISBN 978-0-521-43069-2.
  3. Rudin, Walter (1976). Principles of Mathematical Analysis (вид. 3rd). New York: McGraw-Hill. с. 30. ISBN 0070856133.
  4. Gray, Robert (1994). Georg Cantor and Transcendental Numbers. American Mathematical Monthly 101 (9): 819–832. JSTOR 2975129. doi:10.2307/2975129.
  5. Bloch, Ethan D. (2011). The Real Numbers and Real Analysis. New York: Springer. с. 429. ISBN 978-0-387-72176-7.
  6. Sheppard, Barnaby (2014). The Logic of Infinity (вид. illustrated). Cambridge University Press. с. 73. ISBN 978-1-107-05831-6.
  7. Russell's paradox. Stanford encyclopedia of philosophy.
  8. Bertrand Russell (1931). Principles of mathematics. Norton. с. 363–366.
  9. Keith Simmons (30 липня 1993). Universality and the Liar: An Essay on Truth and the Diagonal Argument. Cambridge University Press. с. 27. ISBN 978-0-521-43069-2.

Зовнішні посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.