Діаграма Юнга

Діаграма Юнга — у математиці є комбінаторним об'єктом, корисним у теорії представлень та численні Шуберта. Діаграма забезпечує зручний спосіб опису представлення групи симетричних та загальних лінійних груп та вивчення їх властивостей. Діаграми Юнга були введені Альфредом Юнгом, математиком Кембриджського університету, в 1900 році.[1][2] Невдовзі, у 1903 році, вони були застосовані у вивченні симетричної групи Георгом Фробеніусом. У подальшому теорія діаграм Юнга була розвинута багатьма математиками, зокрема Персі МакМахонаном, Вільямом Годжем, Г. де Б. Робінсоном, Джан-Карло Ротом, Аленом Ласкуем, Марселем-Поль Шютценбергером та Річардом П. Стенлі.

Визначення

Примітка: ця стаття використовує англійську конвенцію для відображення "Діаграм та таблиць Юнга".

Діаграми

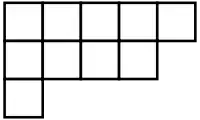
Діаграма Юнга форми (5, 4, 1), англійське позначення

Діаграма Юнга (також називається діаграмою Феррера, особливо, якщо вона представлена з використанням точок) - це скінчена колекція комірок, розташованих у стовпцях, що лежать у лівих-виправданих рядках, з довжинами рядків у незмінному порядку. У переліку кількості кодів у кожному рядку задано розділ $λ$ невід'ємного цілого числа $n$ , загальну кількість кодів діаграми. Схоже, діаграма Юнга має форму $λ$ , і вона містить ту ж саму інформацію, що і цей розділ. Зберігання однієї діаграми Юнга в іншій означає часткове впорядкування на множині всіх розділів, що насправді є структурою гратки, відомої як гратка Юнга. У кожному стовпчику вказано кількість комірок діаграми Юнга, яка дає інший розділ, сполучений або переміщений розділ λ; одержує діаграму Юнга такої форми, яка відбиває оригінальну діаграму вздовж головної діагоналі.

Існує майже загальна згода про те, що в маркуванні комірки діаграми Юнга за парними цілими числами перший індекс вибирає рядок діаграми, а другий індекс вибирає поле в рядку. Тим не менш існують дві чіткі конвенції для відображення цих діаграм: перша розміщує кожен рядок під попереднім, а друга розміщує кожен рядок у верхній частині попереднього. Оскільки перша конвенція в основному використовується англофонами, тоді як вони часто віддають перевагу французьким мовам, звичайно в цій конвенції існує, відповідно, як англійське позначення та французьке позначення; наприклад, у своїй книзі про симетричні функції, Ян Гранд Макдональд радить читачам, які віддають перевагу Французькій конвенції, "читати цю книгу вгору вниз у дзеркалі" (Macdonald 1979, p. 2). Ця номенклатура, мабуть, почалася як жартівлива. Англійське позначення відповідає універсальному використанню матриць, тоді як французьке позначення лише наближається до конвенції декартових координат; однак, французьке позначення відрізняється від цієї конвенції, поставивши в першу чергу вертикальну координату. На малюнку праворуч показано діаграму Юнга , яка відповідає розділу (5, 4, 1) номеру 10 за допомогою англійського позначення. Кон'югативним розділом, який вимірює довжину колонки, є (3, 2, 2, 2, 1).

Довжина руки та ноги

У багатьох програмах, наприклад, при визначенні функцій Джека, зручно визначити довжину руки a_λ(s) комірки s як число стовпців праворуч від s на діаграмі λ. Аналогічно, довжина ноги l_λ(s) - це кількість комірок нижче s. Ця позначка передбачає, використання англійського позначення. Наприклад, значення гака комірки s в λ є тоді це просто a_λ(s)+l_λ(s)+1.

Таблиці

Стандартна діаграма Юнга форми (5, 4, 1)

Таблиці Юнга отримуються, заповненням комірок діаграми Юнга діаграми з символами, взятими з деякого алфавіту, який, як правило, повинен бути повністю впорядкованою множиною. Спочатку цей алфавіт був набором індексованих змінних $x 1$ , $x 2$ , $x 3$ ..., але зараз для зручності зазвичай використовується набір чисел. У своїй оригінальній заявці до теорії представлення симетричної групи, таблиці Юнга мають $n$ різних записів, довільно призначених коміркам діаграми. Таблиця називається стандартною, якщо записи в кожному рядку та кожен стовпчик збільшуються. Число відмінних стандартних таблиць Юнга на $n$ записів дається числами інволюції

1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ... (послідовність A000085^{[недоступне посилання з липня 2019]} в EПЦЧ)

В інших програмах природно, щоб однаковий номер з'явився більше одного разу (або взагалі не з'явився) у таблиці. Таблиця називається напів стандартною або стовпчико-строгою, якщо записи трішки збільшуються вздовж кожного рядка і суворо зменшують кожен стовпчик. Записуючи кількість разів, коли кожне число відображається у табличці, дається послідовність, відома як вага таблиць. Таким чином, стандарт таблиць Юнга являє собою саме напів стандартну таблицю ваги (1,1, ..., 1), яка вимагає, щоб кожне ціле число до $n$ з'являлося рівно один раз.

Варіації

Існує декілька варіантів цього визначення: наприклад, суворого-рядкова таблиця, яка збільшує кількість записів по рядках і збільшує колонки. Також були розглянуті таблички зі зменшувальними записами, зокрема, в теорії плоских перегородок. Існують також узагальнення, такі як таблиця доміно або стрічкова таблиця, в якій декілька комірок можуть бути згруповані разом перед призначенням записів до них.

Асиметричні таблиці

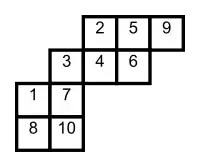
Асиметрична таблиця форми (5, 4, 2, 2)/ (2, 1), англійське позначення

Асиметрична форма являє собою пару розділів ( $λ$ , $μ$ ) таких, що діаграма Юнга $λ$ містить діаграму Юнга $μ$ ; це позначається $λ$ / $μ$ . Якщо $λ$ = ( $λ$ ₁, $λ$ ₂,...) і $μ$ =( $μ$ ₁, $μ$ ₂,...),, то сховище діаграм означає, що $μ i$ ≤ $λ i$ для всіх $i$ . Діаграма асиметричної форми $λ$ / $μ$ - це теоретико-множинна різниця діаграми Юнга та діапазонів $λ$ та $μ$ : множина квадратів, що належать до діаграми $λ$ , але не до $μ$ . Асиметрична таблиця форми $λ$ / $μ$ отримується заповненням квадратів відповідної асиметричної діаграми; така таблиця є напів стандартом, якщо записи в кожному її рядку повільно зростають і суворо збільшуються в кожному стовпчику, і це нормально, якщо всі числа від 1 до числа квадратів асиметричної діаграми з'являються рівно один раз. У той час як карта з розділів на їх діаграму Юнга ін'єктивна, це не так з карти з асиметричною фігурою на асиметричну діаграму; [3] отже, форма асиметричної діаграми не завжди може бути визначена тільки з набору заповнених квадратів. Незважаючи на те, що багато властивостей асиметричних таблиць залежать лише від заповнених квадратів, деякі операції, визначені на них, вимагають явного знання λ та μ, тому важливо, щоб асиметричні таблиці записували цю інформацію: дві різні асиметричні таблиці можуть відрізнятися лише за своєю формою, в той час як вони матимуть один і той же набір квадратів, кожен з яких заповнюється однаковими записами. </ref> therefore the shape of a skew diagram cannot always be determined from the set of filled squares only. Although many properties of skew tableaux only depend on the filled squares, some operations defined on them do require explicit knowledge of $λ$ and $μ$ , so it is important that skew tableaux do record this information: two distinct skew tableaux may differ only in their shape, while they occupy the same set of squares, each filled with the same entries.[4]> Таблиці Юнга можуть бути ідентифіковані з асиметричною таблицею, в якій {{mvar|μ} - порожній розділ (0) (унікальний розділ 0).

Будь-яка напів стандартна таблиця $T$ з формою $λ$ / $μ$ з позитивними цілими записами породжує послідовність розділів (або діаграми Юнга), починаючи з $μ$ , і беручи за розділ $i$ , розміщується далі в послідовності, в якій діаграма отримується з $μ$ , додавши всі поля, що містять значення value ≤ $i$ в $T$ ; цей розділ з часом стає рівним $λ$ . Будь-яка пара послідовних форм у такій послідовності є асиметричною формою, діаграма якої містить не більше одного коду в кожному стовпчику; такі форми називаються горизонтальними смугами. Ця послідовність розділів повністю визначає $T$ , і насправді можна визначити напів стандартною таблицею як такі послідовності, як це робив Макдональд (Macdonald 1979, p. 4).Це визначення включає розділи $λ$ і $μ$ у даних, що містять асиметричну таблицю.

Огляд програм

Таблиці Юнга мають численне застосування в комбінаториці, теорії представлень та алгебраїчній геометрії. Розглянуто різні способи підрахунку "Таблиць Юнга" і доведено спосіб визначення та ідентифікації для функцій Шура. Відомо багато комбінаторних алгоритмів на таблицях, в тому числі Шютценбергера та кореспонденція Робінзона-Шенштейта-Кнута. Ласкукс і Шютценбергер вивчали асоціативний продукт на наборі всіх напів стандартних таблиць Юнга, надавши їм структуру під назвою пластичний моноід (французька: le monoïde plaxique).

У теорії зображень стандартні таблиці Юнга з розміром $k$ описують основи нескоротних уявлень симетричної групи на $k$ букв. Стандартна мономерна основа в кінцевомірному нескоротному представленні загальної лінійної групи $GL n$ параметризована набором напів стандартних таблиць Юнга фіксованої форми над алфавітом {1, 2, ..., $n$ }. Це має важливі наслідки для теорії інваріантів, починаючи від роботи Годжа на однорідному координатному кільці грассманіану який далі досліджує Джан-Карло Рот з співавторами, включаючи Конкіна і Клаудіо Процесі, а також Ейзенбуда. Правило Літлвуда-Річардсона, що описує (серед інших речей) розпад тензорного добутку нескоротних уявлень $GL n$ на нескоротні компоненти, сформульовано в термінах певного асиметричної напівстандартної таблиці.

Застосування до алгебраїчного центру геометрії навколо обчислення Шуберта на грассманіанах та різновидах знаменів. Деякі важливі класи гомології можуть бути представлені поліномами Шуберта та описані в термінах таблиць Юнга.

Застосування в теорії подання

Дивіться також:Теорія представлення симетричної групи

Діаграми Юнга знаходяться в тісному взаємозв'язку з незвідними зображенннями симетричної групи над комплексними числами. Вони забезпечують зручний спосіб визначення симетризаторів Юнга, з яких побудовані незвідні зображення. Багато фактів про зображення можна вивести з відповідної діаграми. Нижче ми описуємо два приклади: визначення розмірності зображення та обмеження зображення. В обох випадках ми побачимо, що деякі властивості представлення можна визначити, використовуючи лише його діаграму.

Діаграми Юнга також параметризують незвідні поліноміальні зображення загальної лінійної групи $GL n$ (коли вони мають не більше $n$ непорожніх рядків) або незвідні зображення спеціальної лінійної групи $SL n$ (коли вони мають не більше $n - 1$ порожніх рядків), або незвідні комплексні зображення спеціальної унітарної групи $SU n$ (знову ж таки, коли вони мають не більше $n - 1$ порожніх рядків). У цих випадках центральну роль відіграє напів стандартна таблиця з записами до $n$ , а не стандартна таблиця; зокрема це число тих таблиць, які визначають розмір представлення.

Розмірність зображення

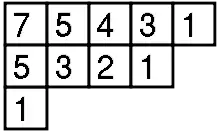
Довжини гаків коробок для перегородки 10 = 5 + 4 + 1

Розмір неcкоротного представлення $π λ$ симетричної групи $S n$ , що відповідає розбиттю $λ$ з $n$ , дорівнює кількості різних стандартних таблиць Юнга, які можна отримати з діаграми представлення. Цей номер можна розрахувати за формулою довжини гачка.

Гачок з довжиною гачка $hook(x)$ комірки $x$ у діаграмі Юнга $Y (λ)$ форми $λ$ - це число комірок, що знаходяться в одному рядку справа від нього, а також ті комірки в тому ж стовпчику під ним, плюс один ( для самої комірки). За формулою довжини гачка розмір нескоротного зображення - $n!$ поділена на виріб довжини гачка всіх комірок у діаграмі подання:

\dim \pi _{\lambda }={\frac {n!}{\prod _{x\in Y(\lambda )}\operatorname {hook} (x)}}.

На малюнку праворуч показано довжини гаків для всіх комірок на діаграмі розділу 10 = 5 + 4 + 1. Таким чином

\dim \pi _{\lambda }={\frac {10!}{7\cdot 5\cdot 4\cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot 1}}=288.

Аналогічно, розмір нескоротного представлення $W (λ)$ $GL r$ , що відповідає розбиттю λ з n (з не більше r частинами), - це число напівстандартного зображення Юнга у формі λ (що містить лише записи від 1 до r), яке задається формулою довжини гачка:

\dim W(\lambda )=\prod _{(i,j)\in Y(\lambda )}{\frac {r+j-i}{\mathrm {hook} (i,j)}},

де індекс i дає рядок і колонку j комірки. [5] Наприклад, розділ (5, 4, 1) ми отримуємо як розмір відповідного нескоротного представлення GL7 (переміщення кодів рядками):

\dim W(\lambda )={\frac {7\cdot 8\cdot 9\cdot 10\cdot 11\cdot 6\cdot 7\cdot 8\cdot 9\cdot 5}{7\cdot 5\cdot 4\cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot 1}}=66528.

Обмежені зображення

Представлення симетричної групи на $n$ елементах, $S n$ також є зображеннями симетричної групи на $n - 1$ елемента $S n -1$ . Однак неприйнятне зображення $S n$ не може бути неприйнятним для $S n -1$ . Натомість це може бути пряма сума декількох уявлень, які нескоротні для Sn-1. Ці уявлення потім називаються факторами обмеженого зображення (див. також Індуковане подання).

Питання про визначення цього розкладу обмеженого представлення даного незвідного зображенням S_n, що відповідає розбиттю $λ$ з $n$ , відповідає наступним чином. Один з них утворює набір всіх діаграм Юнга, які можна отримати з діаграми форми $λ$ , видаливши лише одну комірку (яка повинна бути в кінці його рядка та її стовпчика); потім обмежене представлення розкладається як пряма сума незвідних представлень $S n -1$ , що відповідають тим діаграмам, кожен з яких з'являється лише один раз у сукупності.

Дивіться також

Шур-Вейл подвійність
Решітка Юнга
Листування Робінзон-Шенченд

Примітки

Knuth, Donald E. (1973). The Art of Computer Programming, Vol. III: Sorting and Searching (вид. 2nd). Addison-Wesley. с. 48. «Such arrangements were introduced by Alfred Young in 1900».
Young, A. (1900). On quantitative substitutional analysis. Proceedings of the London Mathematical Society. Ser. 1 33 (1): 97–145. doi:10.1112/plms/s1-33.1.97.. See in particular p. 133.
For instance the skew diagram consisting of a single square at position (2,4) can be obtained by removing the diagram of μ = (5,3,2,1) from the one of λ = (5,4,2,1), but also in (infinitely) many other ways. In general any skew diagram whose set of non-empty rows (or of non-empty columns) is not contiguous or does not contain the first row (respectively column) will be associated to more than one skew shape.
A somewhat similar situation arises for matrices: the 3-by-0 matrix $A$ must be distinguished from the 0-by-3 matrix $B$ , since $AB$ is a 3-by-3 (zero) matrix while $BA$ is the 0-by-0 matrix, but both $A$ and $B$ have the same (empty) set of entries; for skew tableaux however such distinction is necessary even in cases where the set of entries is not empty.
Predrag Cvitanović (2008). Group Theory: Birdtracks, Lie's, and Exceptional Groups. Princeton University Press., eq. 9.28 and appendix B.4

Список літератури

William Fulton. Young Tableaux, with Applications to Representation Theory and Geometry. Cambridge University Press, 1997, ISBN 0-521-56724-6.
Howard Georgi, Lie Algebras in Particle Physics, 2nd Edition - Westview
Macdonald, I. G. Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford, 1979. viii+180 pp. ISBN 0-19-853530-9 MR 553598
Laurent Manivel. Symmetric Functions, Schubert Polynomials, and Degeneracy Loci. American Mathematical Society.
Jean-Christophe Novelli, Igor Pak, Alexander V. Stoyanovkii, "A direct bijective proof of the Hook-length formula", Discrete Mathematics and Theoretical Computer Science 1 (1997), pp. 53–67.
Bruce E. Sagan. The Symmetric Group. Springer, 2001, ISBN 0-387-95067-2
Vinberg, E.B. (2001). Y/y099100. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Predrag Cvitanović, Group Theory: Birdtracks, Lie's, and Exceptional Groups. Princeton University Press, 2008.

Посилання

Eric W. Weisstein. "Ferrers Diagram". From MathWorld—A Wolfram Web Resource.
Eric W. Weisstein. "Young Tableau." From MathWorld—A Wolfram Web Resource.
Semistandard tableaux entry in the FindStat database
Standard tableaux entry in the FindStat database

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Knuth, Donald E. (1973). The Art of Computer Programming, Vol. III: Sorting and Searching (вид. 2nd). Addison-Wesley. с. 48. «Such arrangements were introduced by Alfred Young in 1900».

[2] Young, A. (1900). On quantitative substitutional analysis. Proceedings of the London Mathematical Society. Ser. 1 33 (1): 97–145. doi:10.1112/plms/s1-33.1.97.. See in particular p. 133.

[3] For instance the skew diagram consisting of a single square at position (2,4) can be obtained by removing the diagram of μ = (5,3,2,1) from the one of λ = (5,4,2,1), but also in (infinitely) many other ways. In general any skew diagram whose set of non-empty rows (or of non-empty columns) is not contiguous or does not contain the first row (respectively column) will be associated to more than one skew shape.

[4] A somewhat similar situation arises for matrices: the 3-by-0 matrix $A$ must be distinguished from the 0-by-3 matrix $B$ , since $AB$ is a 3-by-3 (zero) matrix while $BA$ is the 0-by-0 matrix, but both $A$ and $B$ have the same (empty) set of entries; for skew tableaux however such distinction is necessary even in cases where the set of entries is not empty.

[5] Predrag Cvitanović (2008). Group Theory: Birdtracks, Lie's, and Exceptional Groups. Princeton University Press., eq. 9.28 and appendix B.4