Загальна лінійна модель
Зага́льна ліні́йна моде́ль — це статистична лінійна модель, що визначається наступним рівнянням:
| Частина з циклу Статистика |
| Регресійний аналіз |
|---|
 |
| Моделі |
|
|
|
|
|
| Оцінка |
|
|
| Підґрунтя |
|
де Y — це матриця що описує виміри, X — матриця, яка може бути матриця розрахунку, B являє собою матрицю, параметри якої, як правило, повинні бути оцінені, та U являє собою матрицю, яка містить характеристику випадкової помилки або шум. Помилки, як правило, є наслідком багатовимірного нормального розподілу. Якщо помилки не йдуть за багатовимірним нормальним розподілом, узагальнені лінійні моделі можуть бути використані, щоб спростити припущення про Y та U. Загальна лінійна модель включає в себе цілий ряд різних статистичних моделей: ANOVA, ANCOVA, MANOVA, MANCOVA, звичайні лінійної регресії, Т-тест і F-тест. Повна лінійна модель є узагальненням моделі множинної лінійної регресії на випадок більш однієї залежної змінної. Якщо Y, B і U були б вектор-стовпчиками, то матричне рівняння, що наведене вище представлятиме множинну лінійну регресію. Тести гіпотези з загальною лінійною моделлю можуть бути зроблені двома способами: або як багатовимірний або як кілька незалежних одновимірних тестів. У багатовимірному тесті стовпців Y перевіряють разом, тоді як в одновимірному тесті стовпці Y перевіряють незалежно, тобто як безліч одновимірних тестів з тією ж матрицею розрахунку.
Множинна лінійна регресія
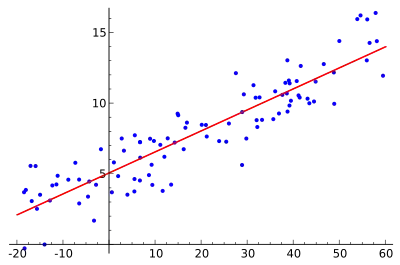
Множинна лінійна регресія є узагальненням лінійної регресії з урахуванням більш ніж однієї незалежної змінної, а окремий випадок загальної лінійної моделі формується за рахунок обмеження кількості залежних змінних до одного. Базовою моделлю для лінійної регресії є:
У наведеній вище формулі ми вважаємо n спостережень одної залежної змінної і p незалежних змінних. Таким чином, Yi спостереження i залежної змінної, Xij є спостереженням j незалежної змінної, j = 1, 2, …, p . Значення β0 є відтинком[2] й інтерпретується як значення залежної змінної Yi, коли усі Хi дорівнюють нулю. Отримуємо:
Значення βj представляють параметри лінійної моделі. Кожен параметр показує, наскільки у середньому зміниться значення залежної змінної при одиничній зміні незалежної змінної, за умови фіксованості усіх інших предикторів. εi є i-та незалежна однаково розподілена нормальна похибка.
Параметри моделі знаходяться методом найменших квадратів. [1]
Застосування
Застосування загальної лінійної моделі з'являється в аналізі численних сканувань головного мозку в наукових експериментах, де Y містить дані від сканерів мозку, X містить експериментальні змінні. Як правило, це перевіряється одновимірним способом (зазвичай названий масово-одномірним в цьому параметрі) і часто згадується як статистичне параметричне відображень.
Див. також
- Haase, Richard; Haase, Richard F. (23 листопада 2011). Multivariate General Linear Models (англ.). SAGE. ISBN 978-1-4129-7249-9.
- intercept // Англійсько-українсько-англійський словник наукової мови (фізика та споріднені науки). Частина І англійсько-українська / уклад. О. Кочерга, Є. Мейнарович. — 2010.
