Регресія Пуассона
У статистиці регресія Пуассона є узагальненою лінійною моделлю регресійного аналізу,який використовувується для моделювання даних та таблиць непередбачених ситуацій.Регресія Пуассона передбачає, що залежна змінна Y має розподіл Пуассона, і припускає, що логарифм її математичного сподівання може бути змодельоване лінійною комбінацією невідомих параметрів. Модель регресії Пуассона іноді називається лог-лінійною моделлю, особливо якщо вона використовується для моделювання таблиці непередбачених ситуацій.
| Частина з циклу Статистика |
| Регресійний аналіз |
|---|
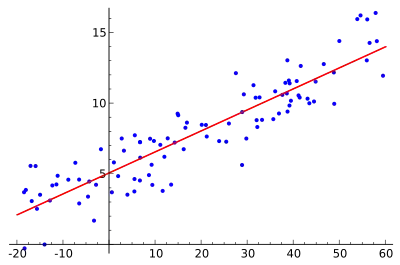 |
| Моделі |
|
|
|
|
|
| Оцінка |
|
|
| Підґрунтя |
|
Негативна біноміальна регресія є узагальненням регресії Пуассона, оскільки вона послаблює сильне припущення, що дисперсія дорівнює середньому значенню, зробленому в моделі Пуассона. Традиційна негативна біноміальна регресійна модель, широко відома як NBA. Вона базується на Пуассон-гамма суміш розподілі. Ця модель популярна, оскільки вона моделює гетерогенність Пуассона за допомогою гамма-розподілу.
Регресійні моделі
Якщо є вектором незалежних змінних, то модель приймає форму
де і .Також цю формулу можна записати як
де x є (n+1) розмірний вектор, який складається з n незалежних змінних, об'єднаних у вектор одиниць.
Тут θ — це .
Таким чином, при заданій регресійній моделі Пуассона θ та вхідному векторі x, передбачуваний середній асоційований розподіл Пуассона, який дано через
Якщо Yi є незалежним спостереженням з відповідними значеннями xi змінних предиктора, то θ можна оцінити за максимальною оцінкою правдоподібності. У максимальній оцінці правдоподібності відсутній вираз із замкнутою формою.