Метод найменших квадратів
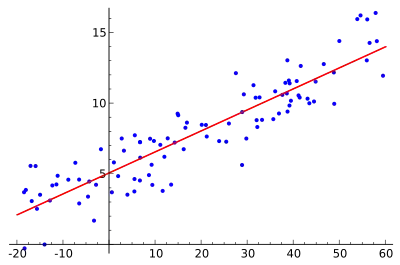
Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується в регресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадку системи лінійних рівнянь. Зокрема важливим застосуванням у цьому випадку є оцінка параметрів у лінійній регресії, що широко застосовується у математичній статистиці і економетриці.
| Частина з циклу Статистика |
| Регресійний аналіз |
|---|
 |
| Моделі |
|
|
|
|
|
| Оцінка |
|
|
| Підґрунтя |
|
Мотиваційний приклад
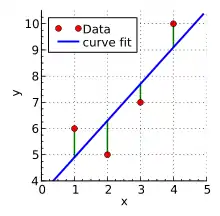
Нехай в результаті деякого досліду отримано чотири точки даних: і (на малюнку ліворуч позначені червоним). Потрібно знайти пряму , яка найкраще підходить для цих точок. Інакше кажучи, ми хотіли б знайти числа і , які приблизно розв'язують надвизначену лінійну систему
чотирьох рівнянь з двома невідомими в деякому найкращому сенсі.
Підхід найменших квадратів розв'язання цієї проблеми полягає у спробі зробити якомога меншою суму квадратів похибок між правою і лівою сторонами цієї системи, тобто необхідно знайти мінімум функції
Мінімум визначають через обчислення часткової похідної від щодо і і прирівнюванням їх до нуля
Це приводить нас до системи з двох рівнянь і двох невідомих, які називаються нормальними рівняннями. Роз'язком СЛАР будуть
- ,
звідки отримуємо , що є рівнянням прямої, яка проходить найближче до поданих чотирьох точок. Мінімальна сума квадратів похибок є
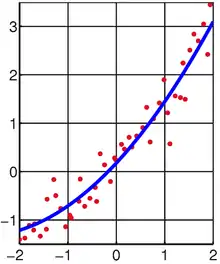
Використання квадратичної моделі
Важливо, що у методі лінійних найменших квадратів ми не обмежені використанням прямої як моделі як у попередньому прикладі. Наприклад, ми могли вибрати обмежену квадратичну модель .[1] Ця модель все ще лінійна в сенсі параметру , отже ми все ще можемо здійснювати той самий аналіз, будуючи систему рівнянь з точок даних:
Часткові похідні щодо параметрів (цього разу лише одного) так само обчислюються і прирівнюються до 0:
Розв'язок отриманого рівняння:
що призводить до визначення найбільш підходящої моделі
Лінійний випадок
Одна незалежна змінна
Нехай маємо лінійну регресію зі скалярною змінною x:
а також вибірку початкових даних розміру M. Тоді
Множинна регресія (випадок багатьох незалежних змінних)
Для надлишково-визначеної системи m лінійних рівнянь з n невідомими
чи в матричній формі запису:
зазвичай не існує точного розв'язку, і потрібно знайти такі β, які мінімізують наступну норму:
Такий розв'язок завжди існує і він є єдиним:
хоч дана формула не є ефективною через необхідність знаходити обернену матрицю.
Виведення формули
Значення досягає мінімуму в точці в якій похідна по кожному параметру рівна нулю. Обчислюючи ці похідні одержимо:
де використано позначення
Також виконуються рівності:
Підставляючи вирази для залишків і їх похідних одержимо рівність:
Дану рівність можна звести до вигляду:
або в матричній формі:
Числові методи для обчислення розв'язку
Якщо матриця є невиродженою та додатноозначеною, тобто має повний ранг, тоді система може бути розв'язана за допомогою розкладу Холецького , де — верхня трикутна матриця.
Розв'язок отримаємо в два кроки:
- Отримаємо з рівняння
- Підставимо і отримаємо з
В обох випадках використовуються властивості трикутної матриці.
Статистичні властивості
Одним із найважливіших застосувань лінійного МНК є оцінка параметрів лінійної регресії. Для заданого набору даних будується модель:
або в матричній формі:
де:
В цих формулах — вектор параметрів, які оцінюються, наприклад, за допомогою методу найменших квадратів, а — вектор випадкових змінних.
У класичній моделі множинної лінійної регресії приймаються такі умови:
- тобто випадкові змінні є гомоскедастичними і між ними відсутня будь-яка залежність.
- Ранг матриці X рівний p + 1, тобто між пояснюючими змінними відсутня лінійна залежність.
Для такої моделі оцінка одержана методом найменших квадратів володіє властивостями:
- Незміщеність. Оцінка є незміщеною, тобто Справді:
- Коваріаційна матриця оцінки рівна:
- Це випливає з того, що і
-
- Ефективність. Згідно з теоремою Гауса — Маркова оцінка, що одержана МНК, є найкращою лінійною незміщеною оцінкою.
- Змістовність. При доволі слабких обмеженнях на матрицю X метод найменших квадратів є змістовним, тобто при збільшенні розміру вибірки, оцінка за імовірністю прямує до точного значення параметру. Однією з достатніх умов є наприклад прямування найменшого власного значення матриці до безмежності при збільшенні розміру вибірки.
- Якщо додатково припустити нормальність змінних то оцінка МНК має розподіл:
В математичному моделюванні
Нехай ми маємо вибірку початкових даних . Функція — невідома.
Якщо ми знаємо приблизний вигляд функції , то задамо її у вигляді функціоналу , де — невідомі константи.
Нам потрібно мінімізувати відмінності між та . Для цього беруть за міру суму квадратів різниць значень цих функцій у всіх точках і її мінімізують (тому метод так і називається):
Коефіцієнти в яких така міра мінімальна знаходять з системи:
Примітки
- Повне квадратне рівняння у загальному випадку має три ненульові коефіцієнти і має вигляд
Джерела
- Лоусон Ч., Хенсон Р. Численное решение задач методом наименьших квадратов. — М.: Наука, 1986.
- Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. — Т. 2: Айвазян С А. Основы эконометрики. — М.: ЮНИТИ- ДАНА, 2001. — 432 с. ISBN 5-238-00305-6
- Björck, Åke (1996). Numerical methods for least squares problems. Philadelphia: SIAM. ISBN 0-89871-360-9.
- Greene, William H. (2002). Econometric analysis (5th ed.). New Jersey: Prentice Hall
Посилання
- Метод найменших квадратів // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 358. — 594 с.
