Біцентричний чотирикутник

Біцентричний чотирикутник — це опуклий чотирикутник, який має як вписане коло, так і описане коло. З визначення випливає, що біцентричні чотирикутники мають всі властивості як описаних чотирикутників, так і вписаних чотирикутників. Інші назви цих чотирикутників: хордо-дотичний чотирикутник[1] і вписано-описаний чотирикутник.

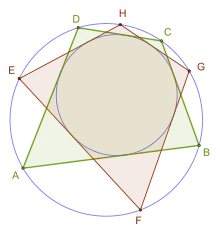
Поризм Понселе для біцентричних чотирикутників ABCD і EFGH

Якщо два кола, одна усередині іншого, є вписаним колом і описаним колом деякого чотирикутника, то будь-яка точка на описаному колі є вершиною якогось (можливо, іншого) біцентричного чотирикутника, який має ті самі вписане та описане кола[2]. Це наслідок поризму Понселе, який довів французький математик Жан-Віктор Понселе (1788-1867).

Спеціальні випадки

Прямокутний дельтоїд[en]

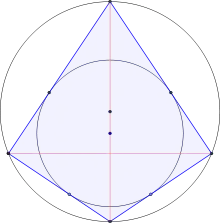
Прикладами вписано-описаних чотирикутників є квадрати, прямокутні дельтоїди[en] і рівнобічні описані трапеції[en].

Опис

Біцентричний чотирикутник ABCD і його контактний чотирикутник WXYZ

Опуклий чотирикутник ABCD зі сторонами a, b, c, d є біцентричним тоді і тільки тоді, коли протилежні сторони задовольняють теоремі Піто для описаних чотирикутників і властивості вписаних чотирикутників, що протилежні кути в сумі дають 180 градусів, тобто,

{\begin{cases}a+c=b+d\\A+C=B+D=\pi .\end{cases}}

Три інших описи стосуються точок, в яких вписане коло в описаному чотирикутнику дотикається до сторін. Якщо вписане коло дотикається сторін AB, BC, CD і DA в точках W, X, Y і Z відповідно, то описаний чотирикутник ABCD є також і описаним в тому і тільки в тому випадку, коли виконується будь-яка з таких трьох умов[3]:

Відрізок WY перпендикулярний до XZ
${\frac {AW}{WB}}={\frac {DY}{YC}}$
${\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}$

Перша з цих трьох умов означає, що контактний чотирикутник WXYZ є ортодіагональним чотирикутником.

Якщо E, F, G, H є серединами WX, XY, YZ, ZW відповідно, то описаний чотирикутник ABCD також є описаним тоді і тільки тоді, коли чотирикутник EFGH є прямокутником[3].

Відповідно до іншого опису, якщо I є центром вписаного кола описаного чотирикутника, у якого продовження протилежних сторін перетинаються в точках J і K, то чотирикутник є описаним тоді і тільки тоді, коли JIK є прямим кутом[3].

Ще однією необхідною і достатньою умовою є те, що описаний чотирикутник ABCD є описаним тоді і тільки тоді, коли його пряма Гаусса перпендикулярна до прямої Гаусса його контактного чотирикутника WXYZ. (Пряма Гаусса чотирикутника визначається середніми точками його діагоналей.)[3]

Побудова

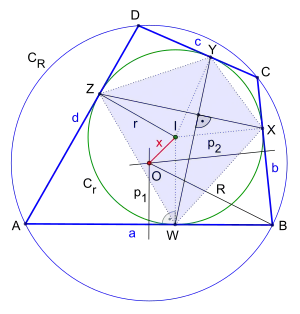
Біцентричний чотирикутник ABCD з контактним чотирикутником WXYZ. Анімацію дивіться тут

Є простий метод побудови біцентричного чотирикутника:

Побудова починається зі вписаного кола C_r з центром I і радіусом r, потім малюємо дві перпендикулярні між собою хорди WY і XZ у вписаному колі C_r. На кінцях хорд проводимо дотичні a, b, c і d до вписаного кола. Вони перетинаються в точках A, B, C і D, які є вершинами біцентричного чотирикутника[4]. Щоб намалювати описане коло, малюємо два перпендикулярні бісектори[en][5] p₁ і p₂ на сторонах біцентричного чотирикутника a і b відповідно. Перпендикулярні бісектори p₁ і p₂ перетинаються в центрі O описаного кола C_R на відстані x від центру I вписаного кола C_r. Описане коло може бути описане навколо центру O.

Правильність цієї побудови випливає з факту, що в описаному чотирикутнику ABCD контактний чотирикутник WXYZ має перпендикулярні діагоналі тоді і тільки тоді, коли описаний чотирикутник є також вписаним.

Площа

Формули в термінах чотирьох величин

Площу K біцентричного чотирикутника можна виразити в термінах чотирьох величин чотирикутника кількома способами. Якщо a, b, c і d є сторонами, то площа задається формулою[2][6][7][8][9]

\displaystyle K={\sqrt {abcd}}.

Це окремий випадок формули Брамагупти. Формулу можна отримати і прямо з тригонометричної формули площі описаного чотирикутника. Зауважимо, що зворотне не виконується — деякі чотирикутники, які не є біцентричними також мають площу $\displaystyle K={\sqrt {abcd}}.$ [10]. Прикладом такого чотирикутника є прямокутник (з різними сторонами, не квадрат).

Площа може бути виражена в термінах відрізків від вершини до точки дотику (для стислості будемо називати ці довжини дотичними довжинами) e, f, g, h[11]

K={\sqrt[{4}]{efgh}}(e+f+g+h).

Формула площі біцентричного чотирикутника ABCD з центром вписаного кола I[7]

K=AI\cdot CI+BI\cdot DI.

Якщо біцентричний чотирикутник має дотичні хорди k, l і діагоналі p, q, тоді він має площу[12]

K={\frac {klpq}{k^{2}+l^{2}}}.

Якщо k, l є дотичними хордами і m, n є бімедіанами чотирикутника, тоді площа може бути обчислена за допомогою формули[7].

K=\left|{\frac {m^{2}-n^{2}}{k^{2}-l^{2}}}\right|kl

Формула не може бути використана, якщо чотирикутник є прямокутним дельтоїдом[en], оскільки в цьому випадку знаменник дорівнює нулю.

Якщо M і N є серединами діагоналей, а E і F є точками перетину продовження сторін, то площа біцентричного чотирикутника задається формулою

K={\frac {2MN\cdot EI\cdot FI}{EF}}

де I є центром вписаного кола[7].

Формули в термінах трьох величин

Площу біцентричного чотирикутника можна виразити в термінах двох протилежних сторін і кута θ між діагоналями згідно з формулою[7]

K=ac\mathrm {tg} \,{\frac {\theta }{2}}=bd\mathrm {ctg} \,{\frac {\theta }{2}}.

У термінах двох суміжних кутів і радіуса r вписаного кола площа задається формулою [7]

K=2r^{2}\left({\frac {1}{\sin {A}}}+{\frac {1}{\sin {B}}}\right).

Площа задається в термінах радіуса R описаного кола і радіуса r вписаного кола як

K=r(r+{\sqrt {4R^{2}+r^{2}}})\sin \theta

де θ є будь-яким з кутів між діагоналями[13].

Якщо M і N є середніми точками діагоналей, а E і F є точками перетину продовжень протилежних сторін, площу можна виразити формулою

K=2MN{\sqrt {EQ\cdot FQ}}

де Q є основою перпендикуляра на пряму EF з центра вписаного кола[7].

Нерівності

Якщо r і R є радіусом вписаного кола і радіусом описаного кола відповідно, тоді площа K задовольняє нерівності[14]

\displaystyle 4r^{2}\leqslant K\leqslant 2R^{2}.

Рівність отримаємо тільки якщо чотирикутник є квадратом.

Іншою нерівністю для площі буде[15]^:p.39,#1203

K\leqslant {\tfrac {4}{3}}r{\sqrt {4R^{2}+r^{2}}}

де r і R є радіусом вписаного кола і радіусом описаного кола відповідно.

Схожа нерівність, що дає точнішу верхню межу для площі, ніж попередня[13]

K\leqslant r(r+{\sqrt {4R^{2}+r^{2}}})

і рівність досягається тоді і тільки тоді, коли чотирикутник є прямокутним дельтоїдом[en].

Крім того, зі сторонами a, b, c, d і півпериметром s:

2{\sqrt {K}}\leqslant qs\leqslant r+{\sqrt {r^{2}+4R^{2}}};

[15]^:p.39,#1203

6K\leqslant ab+ac+ad+bc+bd+cd\leqslant 4r^{2}+4R^{2}+4r{\sqrt {r^{2}+4R^{2}}};

[15]^:p.39,#1203

4Kr^{2}\leqslant abcd\leqslant {\frac {16}{9}}r^{2}(r^{2}+4R^{2}).

[15]^:p.39,#1203

Формули кутів

Якщо a, b, c і d є довжинами сторін AB, BC, CD і DA відповідно у біцентричному чотирикутнику ABCD, то його кути у вершинах можна обчислити за допомогою тангенса[7]:

\mathrm {tg} \,{\frac {A}{2}}={\sqrt {\frac {bc}{ad}}}=\mathrm {ctg} \,{\frac {C}{2}},

\mathrm {tg} \,{\frac {B}{2}}={\sqrt {\frac {cd}{ab}}}=\mathrm {ctg} \,{\frac {D}{2}}.

Якщо використати ті ж позначення, виконуються такі формули для синусів і косинусів[16]:

\sin {\frac {A}{2}}={\sqrt {\frac {bc}{ad+bc}}}=\cos {\frac {C}{2}},

\cos {\frac {A}{2}}={\sqrt {\frac {ad}{ad+bc}}}=\sin {\frac {C}{2}},

\sin {\frac {B}{2}}={\sqrt {\frac {cd}{ab+cd}}}=\cos {\frac {D}{2}},

\cos {\frac {B}{2}}={\sqrt {\frac {ab}{ab+cd}}}=\sin {\frac {D}{2}}.

Кут θ між діагоналями можна обчислити за формулою[8].

\displaystyle \mathrm {tg} \,{\frac {\theta }{2}}={\sqrt {\frac {bd}{ac}}}.

Радіус вписаного кола і радіус описаного кола

Радіус вписаного кола r біцентричного чотирикутника визначається сторонами a, b, c, d за формулою[2]

\displaystyle r={\frac {\sqrt {abcd}}{a+c}}={\frac {\sqrt {abcd}}{b+d}}.

Радіус описаного кола R є окремим випадком формули Парамешвари[2]

\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{abcd}}}.

Радіус вписаного кола можна виразити також у термінах послідовних дотичних довжин e, f, g, h за формулою[17].

\displaystyle r={\sqrt {eg}}={\sqrt {fh}}.

Ці дві формули, фактично, є необхідними і достатніми умовами для описаного чотирикутника з радіусом вписаного кола r бути вписаним.

Чотири сторони a, b, c, d біцентричного чотирикутника є розв'язками рівняння четвертого степеня[en]

y^{4}-2sy^{3}+(s^{2}+2r^{2}+2r{\sqrt {4R^{2}+r^{2}}})y^{2}-2rs({\sqrt {4R^{2}+r^{2}}}+r)y+r^{2}s^{2}=0

де s є півпериметром, а r і R є радіусами вписаного і описаного кіл відповідно[18].

Якщо є біцентричний чотирикутник з радіусом вписаного кола r, дотичні довжини якого дорівнюють e, f, g, h, то існує біцентричний чотирикутник з радіусом вписаного кола r^v, дотичні довжини якого дорівнюють $e^{v},f^{v},g^{v},h^{v}$ , де v можуть бути будь-яким дійсним числом[19].

Біцентричний чотирикутник має більший радіус вписаного кола, ніж будь-який інший описаний чотирикутник, що має ті самі довжини сторін в тій самій послідовності[20].

Нерівності

Радіус описаного кола R і радіус вписаного кола r задовольняють нерівності

R\geqslant {\sqrt {2}}r

яку довів Л. Фейєш Тот у 1948[21]. Нерівність перетворюється на рівність тільки якщо два кола концентричні (центри збігаються). У цьому випадку чотирикутник є квадратом. Нерівність можна довести кількома різними шляхами, один з шляхів використовує подвійну нерівність для площі вище.

Узагальненням попередньої нерівності є[22][23].

{\frac {r{\sqrt {2}}}{R}}\leqslant {\frac {1}{2}}\left(\sin {\frac {A}{2}}\cos {\frac {B}{2}}+\sin {\frac {B}{2}}\cos {\frac {C}{2}}+\sin {\frac {C}{2}}\cos {\frac {D}{2}}+\sin {\frac {D}{2}}\cos {\frac {A}{2}}\right)\leqslant 1

де нерівність перетворюється на рівність тоді і тільки тоді, коли чотирикутник є квадратом[24].

Півпериметр s біцентричного чотирикутника задовольняє[25]

{\sqrt {8r\left({\sqrt {4R^{2}+r^{2}}}-r\right)}}\leqslant s\leqslant {\sqrt {4R^{2}+r^{2}}}+r

де r і R є радіусом вписаного кола і радіусом описаного кола відповідно.

Більше того,[15]^:p.39,#1203

2sr^{2}\leqslant abc+abd+acd+bcd\leqslant 2r(r+{\sqrt {r^{2}+4R^{2}}})^{2}

і

abc+abd+acd+bcd\leqslant 2{\sqrt {K}}(K+2R^{2}).

[15]^:p.62,#1599

Відстань між центром вписаного кола і центром описаного кола

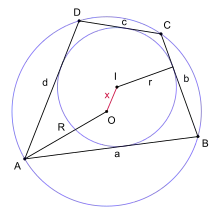
Біцентричний чотирикутник ABCD з центром вписаного кола I і центром описаного кола O

Теорема Фусса

Теорема Фусса дає зв'язок між радіусом вписаного кола r, радіусом описаного кола R і відстанню x між центром вписаного кола I і центром описаного кола O, для будь-якого біцентричного чотирикутника. Зв'язок задається формулою[1][9][26].

{\frac {1}{(R-x)^{2}}}+{\frac {1}{(R+x)^{2}}}={\frac {1}{r^{2}}},

Або, еквівалентно,

\displaystyle 2r^{2}(R^{2}+x^{2})=(R^{2}-x^{2})^{2}.

Формулу вивів М.І.Фусс (1755-1826) у 1792 році. Розв'язуючи відносно x, отримаємо

x={\sqrt {R^{2}+r^{2}-r{\sqrt {4R^{2}+r^{2}}}}}.

Теорема Фусса для вписано-описаних чотирикутників, яка є аналогом теореми Ейлера для трикутників, стверджує, що якщо чотирикутник біцентричений, то його два асоційовані кола пов'язані наведеною вище формулою. Фактично, зворотне також виконується, якщо дано два кола (одне усередині іншого) з радіусами R і r і відстань x між їхніми центрами задовольняє умові теореми Фусса, існує опуклий чотирикутник вписаний в одне з кіл, а інше коло буде вписане в чотирикутник[27] (а тоді за теоремою Понселе, існує нескінченно багато таких чотирикутників).

Якщо скористатись фактом, що $x^{2}\geqslant 0$ у виразі теореми Фусса, отримаємо іншим способом вже згадану нерівність $R\geqslant {\sqrt {2}}r.$ Узагальненням нерівності буде [28]

2r^{2}+x^{2}\leqslant R^{2}\leqslant 2r^{2}+x^{2}+2rx.

Тотожність Карліца

Інша формула відстані x між центрами вписаного кола і описаного кола належить американському математику Леонарду Карліцу (1907-1999). Формула стверджує, що[29].

\displaystyle x^{2}=R^{2}-2Rr\cdot \mu

де r і R є радіусом вписаного кола і радіусом описаного кола відповідно, і

\displaystyle \mu ={\sqrt {\frac {(ab+cd)(ad+bc)}{(a+c)^{2}(ac+bd)}}}={\sqrt {\frac {(ab+cd)(ad+bc)}{(b+d)^{2}(ac+bd)}}}

де a, b, c, d є сторонами біцентричного чотирикутника.

Нерівності для дотичних довжин і сторін

Для дотичних довжин e, f, g, h виконуються такі нерівності[30]:

4r\leqslant e+f+g+h\leqslant 4r\cdot {\frac {R^{2}+x^{2}}{R^{2}-x^{2}}}

і

4r^{2}\leqslant e^{2}+f^{2}+g^{2}+h^{2}\leqslant 4(R^{2}+x^{2}-r^{2})

де r є радіусом вписаного кола, R є радіусом описаного кола, а x є відстанню між центрами цих кіл. Сторони a, b, c, d задовольняють нерівностям[28]

8r\leqslant a+b+c+d\leqslant 8r\cdot {\frac {R^{2}+x^{2}}{R^{2}-x^{2}}}

і

4(R^{2}-x^{2}+2r^{2})\leqslant a^{2}+b^{2}+c^{2}+d^{2}\leqslant 4(3R^{2}-2r^{2}).

Інші властивості центру вписаного кола

Центр описаного кола, центр вписаного кола і точка перетину діагоналей у біцентричному чотирикутнику колінеарні.[31]

Є така рівність щодо чотирьох відстаней між центром вписаного кола I і вершинами біцентричного чотирикутника ABCD:[32]

{\frac {1}{AI^{2}}}+{\frac {1}{CI^{2}}}={\frac {1}{BI^{2}}}+{\frac {1}{DI^{2}}}={\frac {1}{r^{2}}}

де r — радіус вписаного кола.

Якщо точка P є перетином діагоналей у біцентричному чотирикутнику ABCD з центром вписаного кола I, то[33]

{\frac {AP}{CP}}={\frac {AI^{2}}{CI^{2}}}.

Є нерівність для радіуса r вписаного кола і радіуса описаного кола R у біцентричному чотирикутнику ABCD[34]

4r^{2}\leqslant AI\cdot CI+BI\cdot DI\leqslant 2R^{2}

де I є центром вписаного кола.

Властивості діагоналей

Довжини діагоналей у біцентричному чотирикутнику можна виразити в термінах сторін або дотичних довжин. Ці формули правильні для вписаних чотирикутників і описаних чотирикутників відповідно.

У біцентричному чотирикутнику з діагоналями p і q виконується тотожність[9]:

\displaystyle {\frac {pq}{4r^{2}}}-{\frac {4R^{2}}{pq}}=1

де r і R є радіусом вписаного кола і радіусом описаного кола відповідно. Цю тотожність можна переписати як[13]

r={\frac {pq}{2{\sqrt {pq+4R^{2}}}}}

або, розв'язавши її як квадратне рівняння відносно добутку діагоналей, отримаємо

pq=2r\left(r+{\sqrt {4R^{2}+r^{2}}}\right).

Є нерівність для добутку діагоналей p, q у біцентричному чотирикутнику[14]

\displaystyle 8pq\leqslant (a+b+c+d)^{2}

де a, b, c, d — сторони. Нерівність довів Мюррей С. Кламкін у 1967.

Див. також

Біцентричний багатокутник

Примітки

Dörrie, 1965, с. 188–193.
Eric Weisstein, Bicentric Quadrilateral at MathWorld, , Accessed on 2011-08-13.
Josefsson, 2010, с. 165–173.
Alsina, Nelsen, 2011, с. 125–126.
Бисектор відрізка — це пряма, що проходить через його середину
Josefsson, 2010, с. 129.
Josefsson, 2011, с. 155–164.
Durell, Robson, 2003, с. 28, 30.
Yiu, 1998, с. 158-164.
Lord, 2012, с. 345-347.
Josefsson, 2010, с. 128.
Josefsson, 2010a, с. 129.
Josefsson, 2012, с. 237–241.
Alsina, Nelsen, 2009, с. 64–66.
Inequalities proposed in Crux Mathematicorum, 2007.
Josefsson, 2012, с. 79–82.
Radic, Kaliman, Kadum, 2007, с. 41.
Pop, 2009, с. 754.
Radic, 2005, с. 9-10.
Hess, 2014, с. 392–393.
Radic, 2005.
Yun, 2008, с. 119-121.
Shattuck, 2018, с. 141.
Josefsson, 2012, с. 81.
Radic, 2005, с. 13.
Salazar, 2006, с. 306–307.
Byerly, 1909, с. 123–128.
Radic, 2005, с. 5.
Calin, 2010, с. 153–158.
Radic, 2005, с. 3.
Bogomolny, Alex, Collinearity in Bicentric Чотирикутники , 2004.
Juan Carlos Salazar, Fuss Theorem for Bicentric Quadrilateral, 2003, .
Crux Mathematicorum 34 (2008) no 4, p. 242.
Post at Art of Problem Solving, 2009

Література

Heinrich Dörrie. 100 Great Problems of Elementary Mathematics: Their History and Solutions. — New York : Dover, 1965. — С. 188–193. — ISBN 978-0-486-61348-2.
Eric W. Weisstein. Poncelet Transverse // MathWorld – A Wolfram Web Resource,.
Martin Josefsson. Characterizations of Bicentric Quadrilaterals // Forum Geometricorum. — 2010. — Т. 10. — С. 165–173.
Martin Josefsson. Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral // Forum Geometricorum. — 2010a. — Т. 10. — С. 119–130.
Martin Josefsson. The Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2011. — Т. 11. — С. 155–164.
Martin Josefsson. A New Proof of Yun’s Inequality for Bicentric Quadrilaterals // Forum Geometricorum. — 2012. — Т. 12. — С. 79–82.
Claudi Alsina, Roger Nelsen. Icons of Mathematics. An exploration of twenty key images. — Mathematical Association of America, 2011. — С. 125–126. — ISBN 978-0-88385-352-8.
Nick Lord. Quadrilaterals with area formula $\displaystyle K={\sqrt {abcd}}.$ // Mathematical Gazette. — 2012. — Т. 96 (Липень).
Martin Josefsson. Maximal Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2012. — Т. 12. — С. 237–241.
Claudi Alsina, Roger Nelsen. When less is more: visualizing basic inequalities. — Mathematical Association of America, 2009. — С. 64–66. — ISBN 978-0-88385-342-9.
Durell C. V., Robson A. Advanced Trigonometry. — Dover, 2003.
Radic M., Kaliman Z., Kadum V. A condition that a tangential quadrilateral is also a chordal one. — Mathematical Communications, 2007. — Т. 12. — С. 33–52.
Ovidiu T. Pop. Identities and inequalities in a quadrilateral // Octogon Mathematical Magazine. — 2009. — Т. 17, № 2 (Жовтень). — С. 754-763.
Mirko Radic. Certain inequalities concerning bicentric quadrilaterals, hexagons and octagons // Journal of Inequalities in Pure and Applied Mathematics. — 2005. — Т. 6.
Zhang Yun. Euler's Inequality Revisited // Mathematical Spectrum. — 2008. — Т. 40, № 3 (Травень). — С. 119-121.
Mark Shattuck. A Geometric Inequality for Cyclic Quadrilaterals // Forum Geometricorum. — 2018. — Т. 18. — С. 141-154.
Paul Yiu. Euclidean Geometry. — 1998. — С. 158-164.
Juan Carlos Salazar. Fuss's Theorem // Mathematical Gazette. — 2006. — Т. 90 (Липень). — С. 306–307.
Byerly W. E. The In- and-Circumscribed Quadrilateral // The Annals of Mathematics. — 1909. — Т. 10. — С. 123–128. — DOI:10.2307/1967103.
Ovidiu Calin. Euclidean and Non-Euclidean Geometry a metric approach. — 2nd ed.. — Wiley Custom Publishing, 2010. — С. 153–158.
Albrecht Hess. On a circle containing the incenters of tangential quadrilaterals // Forum Geometricorum. — 2014. — Т. 14. — С. 389–396.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTEDörrie1965188–193-1] Dörrie, 1965, с. 188–193.

[Weisstein-2] Eric Weisstein, Bicentric Quadrilateral at MathWorld, , Accessed on 2011-08-13.

[FOOTNOTEJosefsson2010165–173-3] Josefsson, 2010, с. 165–173.

[FOOTNOTEAlsina,_Nelsen2011125–126-4] Alsina, Nelsen, 2011, с. 125–126.

[5] Бисектор відрізка — це пряма, що проходить через його середину

[FOOTNOTEJosefsson2010129-6] Josefsson, 2010, с. 129.

[FOOTNOTEJosefsson2011155–164-7] Josefsson, 2011, с. 155–164.

[FOOTNOTEDurell,_Robson200328,_30-8] Durell, Robson, 2003, с. 28, 30.

[FOOTNOTEYiu1998158-164-9] Yiu, 1998, с. 158-164.

[FOOTNOTELord2012345-347-10] Lord, 2012, с. 345-347.

[FOOTNOTEJosefsson2010128-11] Josefsson, 2010, с. 128.

[FOOTNOTEJosefsson2010a129-12] Josefsson, 2010a, с. 129.

[FOOTNOTEJosefsson2012237–241-13] Josefsson, 2012, с. 237–241.

[FOOTNOTEAlsina,_Nelsen200964–66-14] Alsina, Nelsen, 2009, с. 64–66.

[Crux-15] Inequalities proposed in Crux Mathematicorum, 2007.

[FOOTNOTEJosefsson201279–82-16] Josefsson, 2012, с. 79–82.

[FOOTNOTERadic,_Kaliman,_Kadum200741-17] Radic, Kaliman, Kadum, 2007, с. 41.

[FOOTNOTEPop2009754-18] Pop, 2009, с. 754.

[FOOTNOTERadic20059-10-19] Radic, 2005, с. 9-10.

[FOOTNOTEHess2014392–393-20] Hess, 2014, с. 392–393.

[FOOTNOTERadic2005-21] Radic, 2005.

[FOOTNOTEYun2008119-121-22] Yun, 2008, с. 119-121.

[FOOTNOTEShattuck2018141-23] Shattuck, 2018, с. 141.

[FOOTNOTEJosefsson201281-24] Josefsson, 2012, с. 81.

[FOOTNOTERadic200513-25] Radic, 2005, с. 13.

[FOOTNOTESalazar2006306–307-26] Salazar, 2006, с. 306–307.

[FOOTNOTEByerly1909123–128-27] Byerly, 1909, с. 123–128.

[FOOTNOTERadic20055-28] Radic, 2005, с. 5.

[FOOTNOTECalin2010153–158-29] Calin, 2010, с. 153–158.

[FOOTNOTERadic20053-30] Radic, 2005, с. 3.

[31] Bogomolny, Alex, Collinearity in Bicentric Чотирикутники , 2004.

[32] Juan Carlos Salazar, Fuss Theorem for Bicentric Quadrilateral, 2003, .

[33] Crux Mathematicorum 34 (2008) no 4, p. 242.

[34] Post at Art of Problem Solving, 2009