Розподіл Рейлі
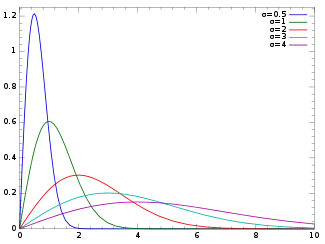
Розподіл Рейлі або розподіл Релея — це розподіл імовірностей випадкової величини із щільністю
| Розподіл Релея | |
|---|---|
 | |
|
Функція розподілу ймовірностей 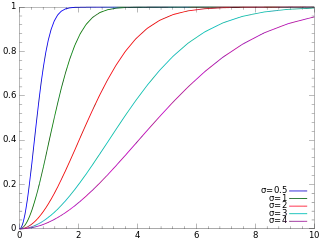 | |
| Параметри | |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Ентропія | |
| Твірна функція моментів (mgf) | |
| Характеристична функція | |
де — параметр масштабу. Відповідна функція розподілу має вигляд
Введено вперше в 1880 р. Джоном Вільямом Стреттом (лордом Релеєм) у зв'язку з задачею додавання гармонійних коливань з випадковими фазами.
Властивості
Моменти випадкової величини з розподілом Релея обчислюються за формулою:
де — Гамма-функція.
Математичне сподівання та дисперсія випадкової величини з розподілом Релея виражається як:
і
Мода дорівнює , а максимум щільності
Коефіцієнт асиметрії задається як:
Формула для обчислення коефіцієнта ексцесу:
Характеристична функція задається формулою:
де — комплексна функція помилок. Формула для твірної функції моментів
де — функція помилок.
Застосування
- У задачах про пристрілювання гармат. Якщо відхилення від цілі для двох взаємно перпендикулярних напрямків нормально розподілені і некорельовані, координати цілі збігаються з початком координат, то позначивши розкид по осях за і , отримаємо вираз величини промаху у формі . У цьому випадку величина має розподіл Релея.
- У радіотехніці для опису амплітудних флуктуацій радіосигналу.
- Щільність розподілу випромінювання абсолютно чорного тіла по частотах.
Зв'язок з іншими розподілами
- Якщо і — незалежні випадкові величини з розподілом Гауса, що мають нульові математичні сподівання і однакові дисперсії , то випадкова величина має розподіл Релея.
- Якщо незалежні Гаусівскі випадкові величини і мають ненульові математичні сподівання, у загальному випадку нерівні, то розподіл Релея переходить у розподіл Райса.
- Щільність розподілу квадрата рейлівскої величини з має розподіл хі-квадрат із двома ступенями свободи.
Див. також
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.