Розподіл Фішера
Розподіл Фішера або F-розподіл у теорії імовірностей — двопараметричне сімейство абсолютно неперервних розподілів. F-розподіл часто зустрічається як розподіл тестової статистики коли нульова гіпотеза вірна, особливо в тесті відношення правдоподібності, найважливіший випадок аналіз дисперсії (див. F-тест).
| Розподіл Фішера | |
|---|---|
 | |
|
Функція розподілу ймовірностей 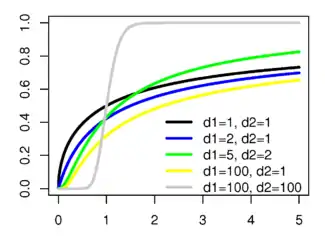 | |
| Параметри | ступені свободи |
| Носій функції | |
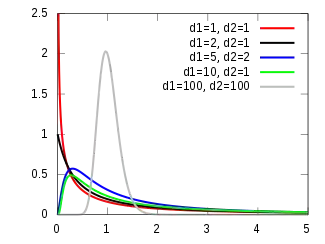
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | для |
| Мода | для |
| Дисперсія | для |
| Коефіцієнт асиметрії |
для |
| Коефіцієнт ексцесу | див. текст |
| Твірна функція моментів (mgf) | не існує, raw moments defined elsewhere[1][2] |
| Характеристична функція | див. текст |
Визначення
Нехай — дві незалежні випадкові величини, що мають розподіл хі-квадрат: , де . Тоді розподіл випадкової величини
- ,
називається розподілом Фішера зі ступенями свободи і . Пишуть .
Щільність випадкової величини з F-розподілом з параметрами задається формулою:
для дійсного числа , тут d1 та d2 цілі додатні числа, а B — Бета-функція.
Моменти
Математичне очікування і дисперсія випадкової величини, що має розподіл Фішера, мають вигляд:
- , якщо ,
- , якщо .
Властивості розподілу Фішера
- Якщо , то
- .
- Розподіл Фішера збігається до одиниці: якщо , то
- по розподілі при ,
де — дельта-функція в одиниці, тобто розподіл випадкової величини-константи .
Зв'язок з іншими розподілами
- Якщо , то випадкові величини збігаються по розподілу до при .
Див. також
Джерела
- Johnson, Norman Lloyd; Samuel Kotz, N. Balakrishnan (1995). Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27). Wiley. ISBN 0-471-58494-0.(англ.)
- Abramowitz, Milton; Stegun, Irene A., ред. (1965). Chapter. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. ISBN 978-0486612720. MR0167642. (англ.)
- Глосарій термінів з хімії // Й.Опейда, О.Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л.М.Литвиненка НАН України, Донецький національний університет — Донецьк: «Вебер», 2008. — 758 с. — ISBN 978-966-335-206-0
