Тривіальні об'єкти в алгебрі

В алгебрі (розділі математики) багато алгебраїчних структур мають тривіальні, тобто найпростіші об'єкти. Як множини, вони складаються з одного елементу, що позначається символом «0», а сам об'єкт — «{0}» або просто «0» залежно від контексту (наприклад, в точних послідовностях). Об'єкти, відповідні тривіальним випадкам, важливі для уніфікації міркувань: наприклад, зручніше сказати, що «рішення рівняння $T x = 0$ завжди складає лінійний простір», ніж робити застереження «... або множина {0}».

Найважливішими з таких об'єктів є:

Тривіальна група, найпростіша з груп. Є також найпростішою з абелевих груп, і всі перелічені нижче об'єкти наслідують її структуру, відому як додавання
Тривіальне кільце, найпростіше з кілець.

Нульовий (тривіальний) модуль, найпростіший з модулів над заданим кільцем $R$ .
Нульовий лінійний простір над полем $R$ , найпростіший з лінійних просторів.
Нульова алгебра, найпростіша з алгебр над кільцем або над полем $R$ .

У трьох останніх випадках множення на скаляр визначається як $κ0 = 0$ , де $κ \in R$ .

Будь-яка нульова алгебра також тривіальна як кільце. Нульова алгебра над полем є нульовим лінійним простором, а над кільцем — нульовим модулем.

Трактування за допомогою теорії категорій

Морфізми в і з нульового об'єкта

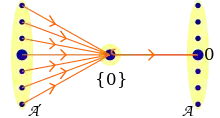
З точки зору теорії категорій, тривіальний об'єкт є термінальним, а іноді (в залежності від визначення морфізму) нульовим (тобто одночасно термінальним і початковим) об'єктом.

Тривіальний об'єкт єдиний з точністю до ізоморфізму.

Термінальність тривіального об'єкта означає, що морфізм $A \to {0}$ існує і єдиний для будь-якого об'єкта $A$ в категорії. Цей морфізм показує будь-який елемент об'єкта $A$ в $0$ .

2↕	${\begin{bmatrix}0\\0\end{bmatrix}}$	=	${\begin{bmatrix}\,\\\,\end{bmatrix}}$	[ ]	<0
	↔ 1		^ 0	↔ 1
Елемент нульового простору, записаний як порожній вектор-стовпець (праворуч), помножений на порожню матрицю 2×0 для отримання 2-вимірного нульового вектора (зліва). З дотриманням правил множення матриць

У категоріях Rng (кілець без обов'язкової одиниці), R-Mod і Vect_$R$, тривіальне кільце, нульові модулі й простір відповідно є нульовими об'єктами. Нульовий об'єкт визначається як початковий, тобто морфізм ${0} \to A$ існує і єдиний для будь-якого об'єкта $A$ в категорії. Цей морфізм показує $0$ , єдиний елемент об'єкта ${0}$ , де $0 \in A$ . Це мономорфізм, і його образ (підмодуль/підпростір в $A$ породжений нулем елементів) ізоморфний {0}.

Структури з одиницею

У структурах з одиницею (нейтральним елементом множення) все не так однозначно. Коли визначення морфізму в категорії вимагає їхнього збереження, тривіальний об'єкт або є тільки термінальним (але не початковим), або відсутній зовсім (наприклад, коли визначення структури вимагає нерівність $1 \neq 0$ ).

У категорії Ring кілець з одиницями, кільце цілих чисел Z початковий об'єкт, а не {0}.

Див. також

Посилання

David Sharpe. Rings and factorization. — Cambridge University Press, 1987. — С. 10 : trivial ring. — ISBN 0-521-33718-6.
Barile, Margherita Trivial Module(англ.) на сайті Wolfram MathWorld.
Barile, Margherita Zero Module(англ.) на сайті Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.