Центр кола дев'яти точок

• Центр кола дев'яти точок ${\displaystyle O_{9}}$ лежить на прямій Ейлера трикутника посередині між ортоцентром ${\displaystyle H}$ і центром описаного кола ${\displaystyle O}$. Центроїд ${\displaystyle M}$ також лежить на цій лінії на відстані 2/3 від ортоцентра до центра описаного кола[2][3], так, що

${\displaystyle O_{9}O=O_{9}H=3O_{9}M~.}$

Таким чином, якщо пара з цих чотирьох центрів відома, положення двох інших легко знайти.

• Ендрю Гінанд 1984 року, досліджуючи задачу, нині відому як задача визначення трикутника Ейлера, показав, що якщо положення цих центрів для невідомого трикутника задано, то інцентр трикутника лежить всередині ортоцентроїдального кола (кола, діаметром якого є відрізок між центроїдом і ортоцентром). Тільки одна точка всередині цього кола не може бути центром вписаного кола — це центр дев'яти точок. Будь-яка інша точка всередині цього кола визначає єдиний трикутник[4][5][6][7].
• Відстань від центра кола дев'яти точок до інцентра ${\displaystyle I}$ задовольняє формулам:

${\displaystyle IO_{9}<{\dfrac {1}{2}}IO~,}$

${\displaystyle IO_{9}={\dfrac {1}{2}}(R-2r)<{\frac {R}{2}}~,}$

${\displaystyle 2R\cdot IO_{9}=OI^{2}~,}$

де ${\displaystyle R}$ і ${\displaystyle r}$ — радіуси описаного і вписаного кіл відповідно.

• Центр кола дев'яти точок є центром описаного кола серединного трикутника, ортотрикутника і трикутника Ейлера[8][3]. Загалом, ця точка є центром описаного кола трикутника, який має вершинами будь-які три з дев'яти перерахованих точок.
• Центр кола дев'яти точок збігається з центроїдом чотирьох точок — трьох точок трикутника і його ортоцентра[9].
• З дев'яти точок на колі Ейлера три є серединами відрізків, що з'єднують вершини з ортоцентром (вершини трикутника Ейлера — Феєрбаха). Ці три точки є відображеннями середин сторін трикутника відносно центра кола дев'яти точок.
• Таким чином, центр кола дев'яти точок є центром симетрії, що переводить серединний трикутник у трикутник Ейлера — Феєрбаха (і навпаки)[3].
• За теоремою Лестер центр кола дев'яти точок лежить на одному колі з трьома іншими точками — двома точками Ферма і центром описаного кола[10].

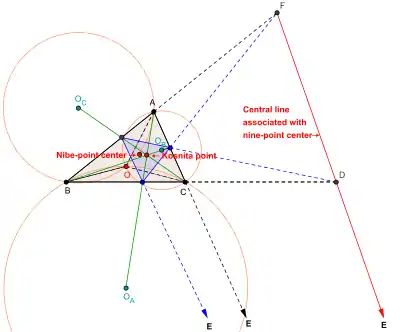
Точка Косніти, ізогонально спряжена центру кола дев'яти точок

• Точка Косніти трикутника, пов'язана з теоремою Косніти, ізогонально спряжена центру кола дев'яти точок[11]. (див. рис.)
• Пряма ${\displaystyle X(485)X(486)}$, що проходить через дві точки Вектена ${\displaystyle X(485)}$ і ${\displaystyle X(486)}$, перетинає пряму Ейлера у центрі дев'яти точок трикутника ${\displaystyle ABC}$.

Трилінійні координати центра кола дев'яти точок рівні[1][2]:

${\displaystyle \cos(B-C):\cos(C-A):\cos(A-B)}$

${\displaystyle =\cos A+2\cos B\cos C:\cos B+2\cos C\cos A:\cos C+2\cos A\cos B}$

${\displaystyle =\cos A-2\sin B\sin C:\cos B-2\sin C\sin A:\cos C-2\sin A\sin B}$

${\displaystyle =bc[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:ca[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:ab[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}]~.}$

Барицентричні координати центра рівні[2]:

${\displaystyle a\cos(B-C):b\cos(C-A):c\cos(A-B)}$

${\displaystyle =a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}~.}$

• Kimberling. Central Points and Central Lines in the Plane of a Triangle // Mathematics Magazine. — 1994. — Т. 67, вип. 3 (26 жовтня).
• Stern. Euler’s triangle determination problem // Forum Geometricorum. — 2007. — Т. 7 (26 жовтня).
• Dekov. Nine-point center // Journal of Computer-Generated Euclidean Geometry. — 2007. — 26 жовтня.
• Euler. Solutio facilis problematum quorundam geometricorum difficillimorum // Novi Commentarii academiae scientiarum Petropolitanae. — 1767. — Т. 11 (26 жовтня).
• Andrew P. Guinand. Euler lines, tritangent centers, and their triangles // The American Mathematical Monthly. — 1984. — Т. 91, вип. 5 (26 жовтня).
• William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Вип. 11 (26 жовтня).
• Paul Yiu. The circles of Lester, Evans, Parry, and their generalizations // Forum Geometricorum. — 2010. — Т. 10 (26 жовтня).
• Rigby. Brief notes on some forgotten geometrical theorems // Mathematics and Informatics Quarterly. — 1997. — Т. 7 (26 жовтня).

• Weisstein, Eric W. Центр кола 9 точок(англ.) на сайті Wolfram MathWorld.