Цифри
Таблиця чисел восьмої сотні
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 |
|---|---|---|---|---|---|---|---|---|---|
| 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 |
| 721 | 722 | 723 | 724 | 725 | 726 | 727 | 728 | 729 | 730 |
| 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 |
| 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 |
| 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 |
| 771 | 772 | 773 | 774 | 775 | 776 | 777 | 778 | 779 | 780 |
| 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 |
| 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
Ци́фри (від арабського «сифр» («нуль»)) — знаки для запису чисел. Цифра це єдиний окремий символ (такий як "2" або "5") що використовується самостійно, або у комбінації з іншими (такій як "25"), для представлення чисел відповідно до правил деякої позиційної системи числення. Слово «цифра» без уточнення зазвичай означає один з таких знаків: 0 1 2 3 4 5 6 7 8 9 (так звані «арабські цифри»). Існують також багато інших варіантів: римські цифри (I V X L C D M), шістнадцяткові цифри (0 1 2 3 4 5 6 7 8 9 A B C D E F), у деяких мовах, наприклад, в івриті, в давньогрецькій та церковнослов'янській мовах, існує система запису чисел буквами.
Тільки у множині слово «цифри» також може означати числові дані. Наприклад, «подамо такі цифри», «цифри середнього значення» (навіть коли йдеться про одне число, вживають множину).
Огляд
У типовій цифровій системі, число представляє собою послідовність цифр, і можуть мати довільну довжину. Кожна позиція в такій послідовності має знакомісце, а кожна цифра має значення. Значення числа розраховується шляхом множення кожної цифри у послідовності на значення, що відповідає знакомісцю і сумуванням результатів.
Значення цифр
Кожна цифра в системі чисел представляє ціле значення. Наприклад, у десятковій системі цифра "1" задає ціле число один, а у шістнадцятковій системі, літера "A" задає число десять. Позиційні системи числення мають мати цифри, що задають цілі значення від нуля до значення її основи, але не включаючи його.
Таким чином, у позиційній десятковій системі, числа від 0 до 9 можна записати відповідними їм цифрами від "0" до "9", де цифра, що записана крайньою праворуч буде знаходитися на позиції, що задає значення "одиниць". Число 12 можна задати цифрою "2" що знаходиться в одиничній позиції, і цифрою "1" в позиції "десятків", ліворуч від "2", а число 312 можна задати трьома цифрами: "3" у позиції "сотень", "1" у позиції "десятків" і "2" у позиції "одиниць".
У Індійсько-арабська система чисел використовують десятковий розділювач, що в деяких регіональних традиціях, наприклад в Англії є крапкою, або в Європі і Україні це кома, для розділення цілої частини і дробової, що позначає знакомісце для одиниць. Кожне знакомісце ліворуч від коми матиме значення аналогічне, як описано вище для звичайного числа де значення цифри множиться на основу системи числення. Аналогічно, кожне наступне значення з правої частини після розділювача буде ділитися на значення основи. Наприклад, для числа 10,34 (представленого у десятковій системі),
- 0 знаходиться одразу ліворуч від розділювача, тобто він знаходиться на знакомісці одиниць;
- 1 ліворуч від одиниць це десятки;
- 3 праворуч від розділювача і ліворуч від одиниць, тому його аналогічно називають місцем, де задаються десяті долі від цілого значення;
- 4 праворуч від десятих, це соті, тобто соте число дробної частини.
Загальне значення числа становить 1 десяток, 0 одиниць, 3 десятих, і 4 сотих. Варто відмітити, що нуль, який не задає ніякого значення числа, необхідний аби зазначити, що цифра 1 знаходиться на місті десяток, а не на знакомісці одиниць.
Значення будь-якої цифри в заданій позиції, що знаходиться в числі можна отримати за допомогою просто розрахунку, який залежить від системи числення. Розрахунок здійснюється шляхом множення даної цифри на базис системи піднесений у степінь n − 1, де n це позиція цифри відносно розділювача; значення n є додатнім (+), але це лише для тих цифр, що знаходяться ліворуч від розділювача. Цифри, що знаходяться праворуч, помножуються на базис піднесений до негативного ступеня (−) n. Наприклад, для числа 10,34 (що задане у десятковій позиційній системі із базисом 10),
- цифра 1 є другою ліворуч від розділювача, тому її значення розраховується наступним чином,
- 4 є другою цифрою праворуч від розділювача, тому її значення розраховується наступним чином,
Історія
Історія стародавніх цифр
Допоміжні засоби для рахування, особливо із застосування частин тіла (рахування на пальцях), звичайно використовувався в доісторичні часи як і сьогодні. Існувало багато варіацій. Крім рахування за допомогою десяти пальців, в деяких культурах рахували фаланги, суглоби і пальці на ногах також. У культурі Оксапмин, що у Новій Гвінеї існує система із 27 різними позиціями верхньої частини тіла для представлення цифр.
Для того, щоб якось записувати числову інформацію, із доісторичних часів використовувалися зарубки на дереві, кістках і камінні. Культури кам'яного віку, включаючи стародавніх індіанців Америки, використовували зарубки для азартних ігор, особистих підрахунків і торгівлі.
Метод записування інформації на глині був винайдений Шумерами між 8000 і 3500 рр до н. е. Вони робили не великі глиняні знаки різної форми, які нанизувалися як бісер на нитку. Починаючи з 3500 р. до н. е., глиняні фігурки були замінені цифровими знаками вдавленими круглим стилусом під різними кутами на глиняних дощечках, які потім запікали. Згодом близько 3100 р. до н. е., письмові цифри перестали пов'язуватися із речами які підраховуються і почали використовуватися як абстрактні числа.
Між 2700 і 2000 р. до н. е., у Шумерів, круглий стилус поступово замінили на загострений, який використовувався для витискання клиноподібних знаків на глині. Ці клиноподібні знаки цифр нагадували круглі знаки, які вони замінили і зберегли принцип додавання круглих числових знаків. Ця система поступово перетворилися на загальну шістдесяткову систему числення; і це була позиційна система цифр, що складалася із лише двох символів: вертикального клина і шеврона, в якій також можна було записувати дріб. Ця шістдесяткова система числення набула повного розвитку у початок періоду Старого Вавилону (приблизно 1950 до н. е.) і стала стандартною у Вавілонії.
Шістдесяткові цифри мали змішану основу. До 1950 до н. е., ця система стала позиційною системою. Шістдесятирічні цифри почали широко використовувати в торгівлі, а також у астрономічних і інших розрахунках. Ця система широко розповсюдилася із Вавілонії і почала використовуватися по всій Месопотамії, та згодом у кожному середземноморському краї використовували стандартні вавилонські одиниці вимірювання і підрахунку, включаючи Грецію, Рим і Єгипет. Вавилонський стиль шістдесяткової нотації досі використовується в сучасному світі для вимірювання часу (хвилин на годину) і кутів (градуси).
Зародження сучасної позиційної системи числення
Першою справжньою письмовою позиційною системою числення вважається була Індійсько-арабська система чисел. Ця система була створена у 7-му столітті в Індії,[1] але ще не мала її сучасної форми, оскільки використання цифри нуль, ще не було загальноприйнятим. Замість нуля, на знакомісці залишали точку. Перше загально визнане використання нуля було уже в 876 р.. Тодішні первотворені цифри буде дуже схожі на сучасні, навіть гліфи що використовувалися для зображення цифр.[1]
До часів 13-го століття, Індо-арабські цифри були прийняті в колах Європейських математиків (Фібоначчі використовував їх у своїй Книзі абака). У загальне користування вони почали входити у 15-му столітті. До кінця 20-го століття практично усі обчислення (не комп'ютеризовані) здійснювалися з використанням арабських цифр, які замінили собою національні цифрові системи більшості культур.
Інші історичні системи числення, що використовували цифри
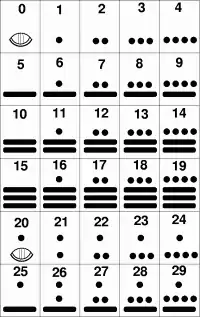
Точний вік Системи числення Майя не відомий, але можливо, що вона була старшою за Індійсько-арабську систему. Ця система була двадцятковою (із основою 20), тому вона мала 20 цифр. Цифрові знаки, які утворювали число, вони записували вертикально, знизу до верху. Оскільки система числення була двадцятковою, то кожна цифра наступної вищої позиції, або порядку, була в двадцять разів більшою від своєї сусідки з нижчої позиції. Якби майя користувалися десятковою системою, ця цифра була б більшою не в двадцять разів, а тільки вдесятеро. На першій позиції (лінійці) стояли одиниці, на другій — двадцятки і т. д. Майя використовували особливий пустий символ для представлення нуля. Вони не мали еквіваленту сучасному десятковому розділювачу, тому в їхній системі не можна було представити дрібні числа.
Тайська система числення є ідентичною до Індійсько-арабської системи числення за виключенням символів, які використовувалися для написання цифр. Викорисатання цих цифр стало менш поширеним у Таїланді ніж це було колись, але вони досі використовуються разом із Індійсько-арабськими числами.
Цифри у вигляді паличок, що були письмовою формою рахункових паличок, що колись використовувалися в Китайській та Японській математиці, були десятковою позиційною системою, в якій можна було представляти не лише нуль а і від'ємні числа. Рахункові палички самі по собі існували раніше ніж Індійсько-арабська система.Цифри Сучжоу є також варіантом цифр у вигляді паличок.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| –0 | –1 | –2 | –3 | –4 | –5 | –6 | –7 | –8 | –9 |
Старослов'янська система числення

У старослов'янській системі числення, до появи сучасних цифр для позначення числових значень використовувалися літери алфавіту. Для того, щоб позначити що якийсь запис із літер, який задає число, зазвичай над кожною літерою або над усією послідовністю літер, що записувала число буквами, ставився особливий знак – титло. Тисячі і сотні позначалися окремим знаком. Така система запису була позиційною і десятковою, де цифри записувалися в тому порядку в якому число читалося. [2]
Національні варіанти арабсько-індійських десяткових цифр
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ٠ | ۰ | ० | ০ | ੦ | ૦ | ୦ | ௦ | ౦ | ೦ | ൦ | ๐ | ໐ | ༠ | ၀ | ០ | ᠐ | ᥆ | ᧐ |
| 1 | ١ | ۱ | १ | ১ | ੧ | ૧ | ୧ | ௧ | ౧ | ೧ | ൧ | ๑ | ໑ | ༡ | ၁ | ១ | ᠑ | ᥇ | ᧑ |
| 2 | ٢ | ۲ | २ | ২ | ੨ | ૨ | ୨ | ௨ | ౨ | ೨ | ൨ | ๒ | ໒ | ༢ | ၂ | ២ | ᠒ | ᥈ | ᧒ |
| 3 | ٣ | ۳ | ३ | ৩ | ੩ | ૩ | ୩ | ௩ | ౩ | ೩ | ൩ | ๓ | ໓ | ༣ | ၃ | ៣ | ᠓ | ᥉ | ᧓ |
| 4 | ٤ | ۴ | ४ | ৪ | ੪ | ૪ | ୪ | ௪ | ౪ | ೪ | ൪ | ๔ | ໔ | ༤ | ၄ | ៤ | ᠔ | ᥊ | ᧔ |
| 5 | ٥ | ۵ | ५ | ৫ | ੫ | ૫ | ୫ | ௫ | ౫ | ೫ | ൫ | ๕ | ໕ | ༥ | ၅ | ៥ | ᠕ | ᥋ | ᧕ |
| 6 | ٦ | ۶ | ६ | ৬ | ੬ | ૬ | ୬ | ௬ | ౬ | ೬ | ൬ | ๖ | ໖ | ༦ | ၆ | ៦ | ᠖ | ᥌ | ᧖ |
| 7 | ٧ | ۷ | ७ | ৭ | ੭ | ૭ | ୭ | ௭ | ౭ | ೭ | ൭ | ๗ | ໗ | ༧ | ၇ | ៧ | ᠗ | ᥍ | ᧗ |
| 8 | ٨ | ۸ | ८ | ৮ | ੮ | ૮ | ୮ | ௮ | ౮ | ೮ | ൮ | ๘ | ໘ | ༨ | ၈ | ៨ | ᠘ | ᥎ | ᧘ |
| 9 | ٩ | ۹ | ९ | ৯ | ੯ | ૯ | ୯ | ௯ | ౯ | ೯ | ൯ | ๙ | ໙ | ༩ | ၉ | ៩ | ᠙ | ᥏ | ᧙ |
A — стандартні європейські, B — арабські, C — східно—арабські, D — деванагарі, E — бенгальскі, F — ґурмукхі, G — гуджараті, H — орія, I — тамільскі, J — телугу, K — каннада, L — малаялі, M — тайські, N — лаоські, O — тибетські, Р — бірманські, Q — кхмерскі, R — монгольські, S — лімбу, T — new tai lue
Цифри у математиці
Не зважаючи на значну роль цифр у описання чисел, вони відносно не є важливими у сучасній математиці. Тим не менш, існує декілька важливих математичних понять, які використовують форму представлення числа як послідовність цифр.
Цифрові корені
Цифровий корінь, це однозначне число, що отримується шляхом сумування усіх цифр заданого числа, потім сумуванням цифр отриманого результату, і так далі доки не залишиться одна єдина цифра в результаті.
Порівнювання за модулем (основою) дев'ять
Порівнювання за основою дев'ять це процедура, що дозволяє перевірити правильність виконаної арифметичної дії. Аби описати його, нехай представляє собою функцію, що розраховує цифровий корінь числа , як описано вище. Даний метод використовує правило, що якщо , тоді . У процесі порівняння за модулем дев'ять, розраховуються обидві частини рівняння, і якщо вони не є рівними, тоді додавання було виконане не вірно.
Реп'юніти і репцифри
Реп'юніти це цілі числа, що представлені однією цифрою 1. Наприклад, 1111 (одна тисяча сто одинадцять) є реп'юнітом. Репцифри є узагальненим поняттям для реп'юнітів; це такі цілі числа, що представлені однією однаковою цифрою. Наприклад, 333 є репцифрою. Основний інтерес, який для математиків складають реп'юніти це прості числа .[3]
Див. також
Примітки
- O'Connor, J. J. and Robertson, E. F. Arabic Numerals. January 2001. Retrieved on 2007-02-20.
- "Українське небо: Студії над історією астрономії в Україні", Інститут прикладних проблем механіки і математики ім. Я. С. Підстригача НАН України, ред. О. Петрука, Львів 2014.
- Weisstein, Eric W. Repunit(англ.) на сайті Wolfram MathWorld.