Четверта проблема Гільберта
Четверта проблема Гільберта — одна з проблем Гільберта, яка стосується основ геометрії. Потрібно «визначити всі, з точністю до ізоморфізму, реалізації систем аксіом класичних геометрій (Евкліда, Лобачевського і еліптичної), якщо видалити з них аксіоми конгруентності, що містять поняття кута, і поповнити ці системи аксіомою нерівності трикутника.»[1]
У випадки двомірної площині, якщо прийняти ще й аксіому неперервності, приходимо до задачі, поставленої Дарбу: «Знайти на площині всі варіаційні задачі, розв'язками яких є всі прямі лінії на площині.»[2]
Плоскі метрики

Має місце теорема Дезарга:
Якщо два трикутника розташовані на площині таким чином, що прямі, які поєднують відповідні вершини трикутників, проходять через одну точку, то три точки, в яких перетинаються продовження трьох пар відповідних сторін трикутників, лежать на одній прямій.
Необхідною умовою для вирішення IV проблеми Гільберта є вимога, щоб метричний простір, який задовольняє умовам цієї проблеми стосовно виконання аксіом, був дезарговим, тобто повинні виконуватися умови:
- якщо простір є двомірним, необхідно, щоб мала місце теорема Дезарга і обернена до неї;
- якщо розмірність простору більше двох, то необхідно, щоб будь-які три точки лежали на одній площині.
Для дезаргових просторів Гамель довів, що будь-який розв'язок проблеми Гільберта можна представити у дійсному проективному просторі або в опуклій області простору якщо визначити конгруентність відрізків через рівність їх довжин в спеціальній метриці, для якої прямі проективного простору є геодезичними лініями.
Такі метрики називаються плоскими або проективними.
Таким чином, розв'язання проблеми Гільберта може бути зведено до задачі конструктивного визначення всіх повних плоских метрик.
Гамель вирішив цю задачу за додаткового припущення, що метрика є регулярною достатньо високого класу.[3] Однак, як показують прості приклади, регулярні плоскі метрики далеко не вичерпують всі плоскі метрики. З аксіом геометрій, що розглядаються, витікає лише неперервність метрик. Тому повне вирішення проблеми Гільберта передбачає конструктивне визначення всіх неперервних плоских метрик.
Передісторія IV проблеми Гільберта
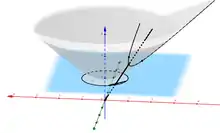
До 1900 року була відома інтерпретація Келі-Клейна геометрії Лобачевського в одиничному колі, де прямими вважаються хорди кола, а відстань між точками визначається як логарифм подвійного відношення чотирьох точок.
Для двовимірних ріманових метрик Е. Бельтрамі (1835—1900) довів, що єдиними плоскими метриками є метрики сталої кривини.[4]
Для багатовимірних ріманових метрик аналогічне твердження було доведено Е. Картаном в 1930 році.
У 1890 році Г. Мінковський при роботі з теорією чисел увів у розгляд те, що ми зараз називаємо скінченновимірними банаховими просторами.[5]
Простір Мінковського
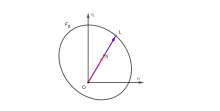
Нехай — компактна замкнена опукла гіперповерхня в евклідовому просторі, задана неявно
Нехай функція задовольняє умовам:
- ;
- ;
- ;
- .
Задамо довжину вектора OA в просторі Мінковського наступним чином:
Простір з такою метрикою називається простором Мінковського.
Гіперповерхня може бути нерегулярною опуклою поверхнею. Метрика, що задається таким чином, є плоскою.
Фінслерів простір
Нехай M — гладкий многовид скінченної вимірності, — дотичне розшарування. Функція буде фінслеровою метрикою, якщо
- ;
- Для будь-якої точки , обмеження функції на є нормою Мінковського.
Тоді називається фінслеровим простором.
Геометрія Гільберта
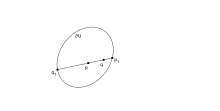
Нехай — обмежена відкрита опукла множина з краєм класу гладкості C2 та додатними нормальними кривинами. Так само, як і для простору Лобачевського, гіперповерхню називають абсолютом геометрії Гільберта.[6]
Метрика Гільберта
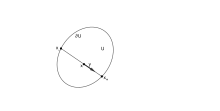
Поверхня індукує фінслерову метрику Гільберта на U для довільних та (див. малюнок)
Ця метрика також є плоскою.
Давід Гільберт увів її в розгляд у 1895 році як узагальнення метрики геометрії Лобачевського. У випадку, коли гіперповерхня є еліпсоїдом, отримуємо геометрію Лобачевського.
Метрика Функа
В 1930 році Функ увів у розгляд несиметричну метрику, яка задається в області обмеженій замкненою опуклою гіперповерхнею і також є плоскою.
σ-метрики
Достатня умова плоских метрик
Перший внесок в рішення IV проблеми Гільберта зробив Гамель. Він довів наступне твердження.[3]
Теорема. Регулярна фінслерова метрика є плоскою тоді, і тільки тоді, коли виконуються умови
Формула Крофтона
Розглянемо множину орієнтованих прямих на площині. Пряма задається параметрами де — відстань до прямої від початку координат, а — кут, який утворює пряма з віссю Ox. Тоді множина орієнтованих прямих гомеоморфна круговому циліндру одиничного радіуса з елементом площі . Нехай — спрямна крива на площині. Тоді її довжина
де — множина прямих, які перетинають цю криву, — число перетинів прямої з кривою. Це встановив М. Крофтон в 1870 році.[7]
Аналогічне твердження виконується і в проективному просторі.
Міра Бляшке-Буземана
У 1966 році Г. Буземан у доповіді на Міжнародному конгресі математиків в Москві, ввів у розгляд новий клас плоских метрик. Він увів на множині прямих проективної площині цілком адитивну невід'ємну міру , яка задовольняє таким умовам:
- , де — множина прямих, що проходять через точку P;
- , де — множина прямих, що проходять через деяку множину X, яка містить відрізок прямої;
- скінченна.
Якщо розглянути -метрику, яка задається в довільній опуклій області проективного простору , то умова 3) замінюється вимогою, щоб для будь-якої множини H, — підмножини , замикання H не перетинається з краєм області , виконувалась умова
- .[8]
За допомогою такої міри визначається -метрика в :
де — множина прямих, які перетинаються відрізок .
Нерівність трикутника для цієї метрики випливає з теореми Паша.
Теорема. -метрика в є плоскою метрикою, тобто, геодезичні в цій метриці є прямими проективного простору.
Але Буземан був далеким від думки, що -метрики вичерпують геть усі плоскі метрики. Він писав: «… Свобода у виборі метрик при заданні геодезичних у випадку неріманових метрик настільки велика, що можна сумніватися, чи дійсно існує переконлива характеристика всіх дезаргових просторів …»[8]
Двовимірний випадок
Теорема Погорєлова
Дивовижною виявилась теорема, доведена в 1973 році О. В. Погорєловим.[9][10]
Теорема. Будь-яка двовимірна неперервна повна плоска метрика є -метрикою.
Тим самим, IV проблема Гільберта для двовимірного випадку була повністю розв'язана.
Доведення Амбарцумяна
У 1976 році Р. Б. Амбарцумян запропонував інше розв'язання IV проблеми Гільберта.[11] Його доведення пов'язано з тим, що в двовимірному випадку міра повністю відновлюється за її значеннями на двокутниках. І тоді вона задається на трикутниках подібно до того, як задається площа трикутника на сфері через кути. На невироджених трикутниках вона додатна, бо виконується нерівність трикутника, після чого міра визначається на всіх борелівських множинах. Але ця конструкція не узагальнюється за розмірністю. Це пов'язано з III проблемою Гільберта, яку вирішив М. Ден. У двовимірному випадку рівновеликі багатокутники є рівноскладеними. У більших вимірностях М. Ден показав, що це не виконується.
Тривимірний випадок
У тривимірному випадку О. В. Погорєлов довів наступну теорему
Теорема. Будь-яка тривимірна регулярна неперервна повна плоска метрика є -метрикою.
Оскільки в тривимірному випадку -міри можуть приймати як додатні, так і від'ємні значення, то необхідними і достатніми умовами того, щоб регулярна метрика, яка задається функцією множини , була плоскою, будуть наступні три умови:
- значення на будь-якій площині дорівнює нулю;
- значення в будь-якому конусі є невід'ємним;
- значення є додатним, якщо конус має внутрішні точки.
Крім того О. В. Погорєлов показав, що будь-яка повна неперервна плоска метрика в тривимірному випадку є межею регулярних -метрик з рівномірною збіжністю в будь-який компактній підобласті, що лежить в області задання цієї метрики. Такі метрики він назвав узагальненими -метриками. Таким чином, О. В. Погорєлову вдалося довести, що
Теорема. Будь-яка повна неперервна плоска метрика в тривимірному випадку є -метрикою в узагальненому сенсі.
Г. Буземан в рецензії на переклад книги О. В. Погорєлова «Четверта проблема Гільберта» писав: «У відповідності з духом тогодення, Гільберт обмежувався вимірностями n = 2, 3. О. В. Погорєлов також обмежився вказаними вимірностями. Хоча існує істотна різниця між n = 2 і n>2. Метод Погорєлова працює і при n>3 лише потребує додаткових технічних подробиць.»[12]
Багатовимірний випадок
Багатовимірний випадок IV проблеми Гільберта досліджувався З. І. Сабо. У 1986 році він довів, як він сам пише, узагальнену теорему Погорєлова:
Теорема. Будь-який n-вимірний простір Дезарга класу породжується конструкцією Бляшке-Буземана.
-міра, які породжує плоску міру, має такі властивості:
- -міра гіперплощин, які проходять через фіксовану точку, дорівнює нулю.
- -міра множини гіперплощин, які перетинають два відрізки [x, y], [y, z], де x, y та z не колінеарні, є додатною.
У цій же статті наведено приклад плоскої метрики, що не породжується конструкцією Бляшке-Буземана. З. І. Сабо описав всі неперервні плоскі метрики за допомогою узагальнених функцій.[13]
IV проблема Гільберта й опуклі тіла
IV проблема Гільберта тісно пов'язана з властивостями опуклих тіл. Опуклий багатогранник називається зонотопом, якщо він є сумою (в сенсі Мінковського) відрізків. Опукле тіло, яке є границею зонотопів у метриці Бляшке-Гаусдорфа, називається зоноїдом. Для зоноїдів опорна функція представляється у вигляді
де — парна додатна міра Бореля на сфері .
Простір Мінковського породжується конструкцією Бляшке-Буземана тоді, і лише тоді, коли опорна функція індикатриси має вигляд наведений вище, де — парна, не обов'язково сталого знаку міра Бореля.[14] Тіла, обмеженими такими гіперповерхнями, називаються узагальненими зоноїдами.
Октаедр в евклідовому просторі не є узагальненим зоноїдом. Тоді з наведеного вище твердження, отримуємо, що плоска метрика простору Мінковського з нормою , не породжується конструкцією Бляшке-Буземана.
Узагальнення IV проблеми Гільберта
Знайдено відповідність між плоскими n-мірними фінслеровими метриками та спеціальними симплектичними формами на грасмановому многовиді в .[15]
Розглядалися періодичні розв'язки IV проблеми Гільберта:
- Нехай (M, g) — компактний локально евклідовий риманів многовид. Припустимо, що на M задана фінслерова метрика, геодезичні якої збігаються з геодезичними метрики g. Тоді ця фінслерова метрика є сумою локально метрики Мінковського та замкнутої 1-форми.[16]
- Нехай (M, g) — компактний симетричний риманів простір рангу більше одного. Якщо F — симетрична фінслерова метрика, геодезичні якої збігаються з геодезичними ріманової метрики g, то (M, F) — симетричний фінслерів простір.[16]
Інший виклад IV проблеми Гільберта є в роботі Пайви 2003 року.[17]
Невирішені задачі
- Не вирішена IV проблема Гільберта для несиметричної відстані.
- Не відомий аналог останньої теореми для випадку симетричних просторів рангу один.
- Описати метрики на , для яких k-площини мінімізують k-площу (Г. Буземан).[18]
Література
- D. Hilbert, Mathematische Probleme, Gottinger Nachrichten, 1900, 253—297.
- G. Darboux, Lecons sur la theorie generale des surfaces, V.III, Paris, 1894.
- G. Hamel, Uber die Geometrien in denen die Geraden die Kurzesten sind, Math. Ann. 57 (1903), 221—264.
- E. Beltrami, Risoluzione del Problema: Riportare i punti di una superficie sobra un piano in modo che le linee geodetiche Vengano rappresentate da linee rette, Annali di Matematica Pura ed Applicata, № 7 (1865), 185—204.
- H. Minkowski, Geometrie der Zahlen, Lpz.-B., 1953.
- D. Hilbert, Uber die gerade Linie als kurzeste Verbindung zweier Punkte, Math. Ann., 46 (1895), 91-96.
- L. A. Santalo, Integral geometry.- In: Studies in Global Geometry and Analysis (S. S. Chern, ed.), Washington, D. C.: Math. Asoc. Amer, 147—195.
- Г. Буземан, Геометрия геодезических, Москва, 1962.
- А. В. Погорелов, Полное решение IV проблемы Гильберта, ДАН СССР № 208, т.1 (1973), 46-49. English translation: A.V. Pogorelov, A complete solution of "Hilbert's fourth problem, Dokl. Acad. Nauk SSR, Vol. 208, № 1 (1973), 48-52.
- А. В. Погорелов, Четвертая Проблема Гильберта. Вид. Наука, 1974. English translation: A.V. Pogorelov, Hilbert's Fourth Problem, Scripta Series in Mathematics, Winston and Sons, 1979.
- R. V. Ambartzumian, A note on pseudo-metric on the plane, Z. Wahrscheinlichkeits theor. Verw. Geb. 37(1976), 145—155.
- H. Busemann, Review of: A. V. Pogorelov, Hilbert's fourth problem, Bull. Amer. Math. Soc. (N. S.) Vol. 4, № 1 (1981), 87-90.
- Z. I. Szabo, Hilbert's fourth problem I, Adv. Math. 59 (1986), 185—301.
- R. Alexander, Zonoid theory and Hilbert fourth problem, Geom. Dedicata 28, № 2 (1988), 199—211.
- J. C. Alvarez Paiva, Sympletic geometry and Hilbert fourth problem, J. Differ. Geom. 69, № 2 (2005), 353—378.
- J. C. Alvarez Pavia and J. Barbosa Gomes, Periodic Solutions of Hilbert fourth problem, 20 pp. arXiv:1809.02783v1[math.MG], 2018.
- J. C. Alvarez Paiva, Hilbert fourth problem in two dimensions I, in: MASS selecta: teaching and learning advanced undergraduate mathematics, ed. S. Katok et al, Providence, RI, AMS, (2003), 165—183.
- A. Papadopoulos, On Hilbert fourth problem, 1-43. Handbook of Hilbert geometry (A. Papadopoulos and M. Troyanov, ed.), European Mathematical Society, IRMA Lectures in Mathematics and Theoretical Physics, № 22 (2014), p. 460.