Число Пелля

Число Пелля — ціле число, що входить як знаменник у нескінченну послідовність відповідних дробів для квадратного кореня з двох. Ця послідовність наближень починається наступним чином: $1/1,3/2,7/5,17/12,41/29,\dots$ , тобто перші числа Пелля — 1, 2, 5, 12 і 29. Чисельники тієї самої послідовності наближень є половинами супутних чисел Пелля або числами Пелля — Люка — нескінченої послідовності, що починається з 2, 6, 14, 34 і 82.

Обидві послідовності, числа Пелля і супутні числа Пелля можуть бути обчислені за допомогою рекурентної формули, схожої на формули для чисел Фібоначчі, і обидві послідовності чисел зростають експоненціально, пропорційно ступеня срібного перетину $1+{\sqrt {2}}$ . Крім використання в ланцюговому дробу наближень до квадратного кореня з двох, числа Пелля можуть бути використані для пошуку квадратних трикутних чисел і для вирішення деяких комбінаторних задач перерахування.[1]

Послідовність чисел Пелля відома з давніх часів. Як і рівняння Пелля, числа Пелля були помилково приписані Леонардом Ейлером Джону Пеллю. Числа Пелля — Люка названі на честь Едуарда Люка, який вивчав ці послідовності. І числа Пелля, і супутні числа Пелля є окремими випадками послідовностей Люка.

Числа Пелля

Числа Пелля задаються лінійним рекурентним співвідношенням:

P_{n}={\begin{cases}0,n=0;\\1,n=1\\2P_{n-1}+P_{n-2},n>1\end{cases}}

і є окремим випадком послідовності Люка.

Перші кілька чисел Пелля

7, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, … (послідовність A000129 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).

Числа Пелля можна виразити формулою

P_{n}={\frac {(1+{\sqrt {2}})^{n}-(1-{\sqrt {2}})^{n}}{2{\sqrt {2}}}}.

Для великих значень n член $\scriptstyle (1+{\sqrt {2}})^{n}$ домінує в цьому виразі, так що числа Пелля приблизно пропорційні ступені срібного перетину $\scriptstyle (1+{\sqrt {2}})$ , також як швидкість росту чисел Фібоначчі дорівнює ступені золотого перетину.

Можливо і третє визначення — у вигляді матричної формули

{\begin{pmatrix}P_{n+1}&P_{n}\\P_{n}&P_{n-1}\end{pmatrix}}={\begin{pmatrix}2&1\\1&0\end{pmatrix}}^{n}.

Багато тотожностей можуть бути доведені з цих визначень, наприклад тотожність, аналогічне тотожності Кассіні для чисел Фібоначчі,

P_{n+1}P_{n-1}-P_{n}^{2}=(-1)^{n},

як негайний наслідок матричної формули (підставляючи визначники матриць ліворуч і праворуч).[2]

Наближення до квадратному кореню з двох

Раціональне наближення до правильних восьмикутників, з координатами з чисел Пелля

Числа Пелля виникли історично з раціональних наближень до квадратного кореня з двох. Якщо два великих цілих x і y дають рішення рівняння Пелля

\displaystyle x^{2}-2y^{2}=\pm 1,

то їх відношення ${\tfrac {x}{y}}$ дає близьке наближення до $\scriptstyle {\sqrt {2}}$ . Послідовність наближень цього виду

1,{\frac {3}{2}},{\frac {7}{5}},{\frac {17}{12}},{\frac {41}{29}},{\frac {99}{70}},\dots

де знаменник кожного дробу — число Пелля і чисельник дорівнює сумі числа Пелля і його попередника в послідовності. Таким чином, наближення мають вигляд ${\tfrac {P_{n-1}+P_{n}}{P_{n}}}$ .

Наближення

{\sqrt {2}}\approx {\frac {577}{408}}

цього типу було відомо математикам Індії в третьому-четвертому столітті до нашої ери.[3] Грецькі математики п'ятого століття до нашої ери також знали про це наближення.[4] Платон (Plato) посилається на чисельники як раціональні діаметри.[5] У другому столітті нашої ери Теон Смирнський використовував терміни сторона і діаметр для опису знаменника і чисельника цієї послідовності.[6]

Ці наближення можуть бути отримані з ланцюгового дробу $\scriptstyle {\sqrt {2}}$ :

{\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots \,}}}}}}}}}}.

Кінцева частина ланцюгового дробу дає апроксимацію у вигляді чисел Пелля. Наприклад,

{\frac {577}{408}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2}}}}}}}}}}}}}}.

Як писав Кнут (1994), факт апроксимації числами Пелля $\scriptstyle {\sqrt {2}}$ дозволяє використовувати їх для раціонального наближення до правильного [[восьмикутник] у з координатами вершин $(\pm P_{i},\pm P_{i+1})$ и $(\pm P_{i+1},\pm P_{i})$ . Всі вершини цього восьмикутника однаково віддалені від центру і формують майже однакові кути. Також точки $(\pm (P_{i}+P_{i-1}),0)$ , $(0,\pm (P_{i}+P_{i-1}))$ и $(\pm P_{i},\pm P_{i})$ формують восьмикутник, у якого вершини майже однаково віддалені від центру і формують однакові кути.

Прості і квадрати

Простим числом Пелля називається число Пелля, що є також простим. Кілька перших простих чисел Пелля

2, 5, 29, 5741, … (послідовність A086383 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

Як і у випадку з числами Фібоначчі, число Пелля $P_{n}$ може бути простим тільки якщо n саме просто.

Є всього три числа Пелля, які є квадратами, кубами та іншими вищими ступенями, — це 0, 1, і 169 = 13². [7]

Незважаючи на те, що мається настільки мало квадратів і інших ступенів серед чисел Пелля, вони мають близький зв'язок з квадратними трикутними числами.[8] Ці числа виникають із наступного тотожності:

{\bigl (}(P_{k-1}+P_{k})\cdot P_{k}{\bigr )}^{2}={\frac {(P_{k-1}+P_{k})^{2}\cdot \left((P_{k-1}+P_{k})^{2}-(-1)^{k}\right)}{2}}.

Ліва частина цієї тотожності дає квадратне число, в той час як права частина дає трикутне число, так що в результаті отримаємо квадратне трикутне число.

Сантана (Santana) і Діац-Барреро (Diaz-Barrero) (2006) довели інше тотожність, що зв'язує числа Пелля з квадратами, показавши, що сума чисел Пелля до $P_{4n+1}$ завжди квадрат:

\sum _{i=0}^{4n+1}P_{i}=\left(\sum _{r=0}^{n}2^{r}{2n+1 \choose 2r}\right)^{2}=(P_{2n}+P_{2n+1})^{2}.

Наприклад, сума чисел Пелля до $P_{5}$ , $0+1+2+5+12+29=49$ , є квадратом числа $P_{2}+P_{3}=2+5=7$ .

Числа $P_{2n}+P_{2n+1}$ , які утворюють квадратні корені таких сум,

1, 7, 41, 239, 1393, 8119, 47321, … (послідовність A002315 з Онлайн енциклопедії послідовностей цілих чисел, OEIS), відомі як прості числа Ньюмена-Шенкса-Вільямса.

Піфагорові трійки

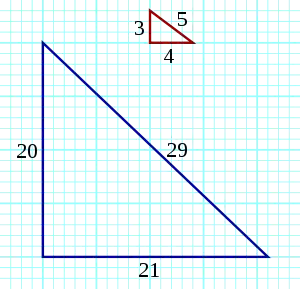
Прямокутні трикутники з майже рівними катетами і цілочисельними координатами, породжені числами Пелля.

Якщо прямокутний трикутник має сторони a, b, c (по теоремі Піфагора a²+b²=c²), то (a,b,c) відомі як піфагорові трійки. Мартін (Martin) (1875) пише, що числа Пелля можуть бути використані для формування піфагорових трійок, в яких a і b відрізняються на одиницю, що відповідає майже рівнобедреного прямокутного трикутника. Кожна така трійка має вигляд

(2P_{n}P_{n+1},P_{n+1}^{2}-P_{n}^{2},P_{n+1}^{2}+P_{n}^{2}=P_{2n+1}).

Послідовність піфагорових трійок, отриманого таким способом: (4,3,5), (20,21,29), (120,119,169), (696,697,985), ….

Числа Пелля — Люка

Супутні числа Пелля або числа Пелля — Люка визначаються лінійним рекурентним співвідношенням:

Q_{n}={\begin{cases}2,n=0\\2,n=1\\2Q_{n-1}+Q_{n-2},n>1\end{cases}}

Тобто, перші два числа в послідовності рівні 2, а всі інші формуються як сума подвоєного попереднього числа Пелля-Люка і попереднього йому, або, що еквівалентно, додаванням наступного числа Пелля і попереднього числа. Так, супутим для 82 є число 29, і 82 = 2 · 34 + 14 = 70 + 12.

Супутні числа Пелля утворюють послідовність:

2, 2, 6, 14, 34, 82, 198, 478, … (послідовність A002203 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

Супутні числа Пелля можна виразити формулою:

Q_{n}=(1+{\sqrt {2}})^{n}+(1-{\sqrt {2}})^{n}.

Всі ці числа парні, кожне з них є подвоєним чисельником у наближенні раціональними числами до $\scriptstyle {\sqrt {2}}$ .

Обчислення та зв'язки

Наступна таблиця дає декілька перших ступенів срібного перетину $\delta =\delta _{S}=1+{\sqrt {2}}$ і зв'язаного з ним ${\bar {\delta }}=1-{\sqrt {2}}$ .

$n$	$(1+{\sqrt {2}})^{n}$	$(1-{\sqrt {2}})^{n}$
0	$1+0{\sqrt {2}}=1.0$	$1-0{\sqrt {2}}=1.0$
1	$1+1{\sqrt {2}}=2.41421\ldots$	$1-1{\sqrt {2}}=-0.41421\ldots$
2	$3+2{\sqrt {2}}=5.82842\ldots$	$3-2{\sqrt {2}}=0.17157\ldots$
3	$7+5{\sqrt {2}}=14.07106\ldots$	$7-5{\sqrt {2}}=-0.07106\ldots$
4	$17+12{\sqrt {2}}=33.97056\ldots$	$17-12{\sqrt {2}}=0.02943\ldots$
5	$41+29{\sqrt {2}}=82.01219\ldots$	$41-29{\sqrt {2}}=-0.01219\ldots$
6	$99+70{\sqrt {2}}=197.9949\ldots$	$99-70{\sqrt {2}}=0.0050\ldots$
7	$239+169{\sqrt {2}}=478.00209\ldots$	$239-169{\sqrt {2}}=-0.00209\ldots$
8	$577+408{\sqrt {2}}=1153.99913\ldots$	$577-408{\sqrt {2}}=0.00086\ldots$
9	$1393+985{\sqrt {2}}=2786.00035\ldots$	$1393-985{\sqrt {2}}=-0.00035\ldots$
10	$3363+2378{\sqrt {2}}=6725.99985\ldots$	$3363-2378{\sqrt {2}}=0.00014\ldots$
11	$8119+5741{\sqrt {2}}=16238.00006\ldots$	$8119-5741{\sqrt {2}}=-0.00006\ldots$
12	$19601+13860{\sqrt {2}}=39201.99997\ldots$	$19601-13860{\sqrt {2}}=0.00002\ldots$

Коефіцієнти являють собою половини супутніх чисел Пелля $H_{n}$ і числа Пелля $P_{n}$ , є невід'ємними рішеннями рівняння $H^{2}-2P^{2}=\pm 1$ .

Квадратне трикутне число — це число $N={\frac {t(t+1)}{2}}=s^{2}$ , яке є як $t\,$ трикутним числом так і $s\,$ квадратним. Майже рівнобедрені піфагорові трійки є цілими рішеннями $a^{2}+b^{2}=c^{2}$ , де $a+1=b$ .

Наступна таблиця показує розкладання непарних $H_{n}$ на дві майже однакові половинки, що дає квадратне трикутне число коли n парне і майже рівнобедрену піфагорову трійку, коли n непарній.

$n$	$H_{n}$	$P_{n}$	t	t+1	s	a	b	c
0	1	0	0	0	0
1	1	1				0	1	1
2	3	2	1	2	1
3	7	5				3	4	5
4	17	12	8	9	6
5	41	29				20	21	29
6	99	70	49	50	35
7	239	169				119	120	169
8	577	408	288	289	204
9	1393	985				696	697	985
10	3363	2378	1681	1682	1189
11	8119	5741				4059	4060	5741
12	19601	13860	9800	9801	6930

Визначення

Половини супутніх чисел Пелля $H_{n}$ і числа Пелля $P_{n}$ можуть бути отримані декількома еквівалентними шляхами:

Піднесення до степеню:

(1+{\sqrt {2}})^{n}=H_{n}+P_{n}{\sqrt {2}}

(1-{\sqrt {2}})^{n}=H_{n}-P_{n}{\sqrt {2}}.

Звідки випливає:

H_{n}={\frac {(1+{\sqrt {2}})^{n}+(1-{\sqrt {2}})^{n}}{2}}.

і

P_{n}{\sqrt {2}}={\frac {(1+{\sqrt {2}})^{n}-(1-{\sqrt {2}})^{n}}{2}}.

Парні рекурентні відношення:

H_{n}={\begin{cases}1,n=0\\H_{n-1}+2P_{n-1},n>0\end{cases}}

P_{n}={\begin{cases}0,n=0;\\H_{n-1}+P_{n-1},n>0\end{cases}}

або, в матричному вигляді:

{\begin{pmatrix}H_{n}\\P_{n}\end{pmatrix}}={\begin{pmatrix}1&2\\1&1\end{pmatrix}}{\begin{pmatrix}H_{n-1}\\P_{n-1}\end{pmatrix}}={\begin{pmatrix}1&2\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}1\\0\end{pmatrix}}.

Таким чином

{\begin{pmatrix}H_{n}&2P_{n}\\P_{n}&H_{n}\end{pmatrix}}={\begin{pmatrix}1&2\\1&1\end{pmatrix}}^{n}.

Наближення

Різниця $H_{n}\,$ і $P_{n}{\sqrt {2}}$ дорівнює $(1-{\sqrt {2}})^{n}\approx (-0.41421)^{n}$ , що швидко наближається до нуля.

Таким чином $(1+{\sqrt {2}})^{n}=H_{n}+P_{n}{\sqrt {2}}$ дуже близьке до $2H_{n}\,$ .

З цього спостереження випливає, що відношення цілих ${\frac {H_{n}}{P_{n}}}$ швидко наближається до ${\sqrt {2}}\,$ у той час як ${\frac {H_{n}}{H_{n-1}}}\,$ и ${\frac {P_{n}}{P_{n-1}}}\,$ швидко наближається до $1+{\sqrt {2}}\,$ .

H² − 2P² = ±1

Оскільки ${\sqrt {2}}$ є ірраціональним, ми не можемо отримати ${\frac {H}{P}}=2\,$ , то есть ${\frac {H^{2}}{P^{2}}}={\frac {2P^{2}}{P^{2}}}\,$ . Найкраще, що ми можемо отримати, це або ${\frac {H^{2}}{P^{2}}}={\frac {2P^{2}-1}{P^{2}}}\,$ або ${\frac {H^{2}}{P^{2}}}={\frac {2P^{2}+1}{P^{2}}}$ .

Невід'ємними рішеннями $H^{2}-2P^{2}=1\,$ є пари $H_{n},P_{n}$ з парним n, і рішеннями $H^{2}-2P^{2}=-1\,$ є пари $H_{n},P_{n}$ з n непарним.

Щоб зрозуміти це, зауважимо

H_{n+1}^{2}-2P_{n+1}^{2}=(H_{n}+2P_{n})^{2}-2(H_{n}+P_{n})^{2}=-(H_{n}^{2}-2P_{n}^{2})\,

так що, починаючи з $H_{0}^{2}-2P_{0}^{2}=1\,$ знак чергується ( $1,-1$ ). Зауважимо тепер, що кожне позитивне рішення можна отримати з рішення з меншим індексом завдяки рівності $(2P-H)^{2}-2(H-P)^{2}=-(H^{2}-2P^{2})\,$ .

Квадратні трикутні числа

Необхідну рівність ${\frac {t(t+1)}{2}}=s^{2}\,$ еквівалентно $4t^{2}+4t+1=8s^{2}+1\,$ , що перетворюється в $H^{2}=2P^{2}+1$ при підстановці $H=2t+1$ і $P=2s$ . Звідси n-м рішенням буде $t_{n}={\frac {H_{2n}-1}{2}}$ і $s_{n}={\frac {P_{2n}}{2}}.$

Зауважимо, що $t$ і $t+1$ взаємно прості, так що ${\frac {t(t+1)}{2}}=s^{2}\,$ можливо тільки тоді, коли вони є сусідніми цілими, одне — квадрат $H^{2}$ й інше — подвоєний квадрат $2P^{2}$ .

Оскільки ми знаємо всі рішення рівняння, ми отримуємо

t_{n}={\begin{cases}2P_{n}^{2}&n\equiv 0{\pmod {2}}\\H_{n}^{2}&n\equiv 1{\pmod {2}}\end{cases}}

і $s_{n}=H_{n}P_{n}\,$

$n$	$H_{n}$	$P_{n}$	t	t+1	s	a	b	c
0	1	0
1	1	1	1	2	1	1	0	1
2	3	2	8	9	6	3	4	5
3	7	5	49	50	35	21	20	29
4	17	12	288	289	204	119	120	169
5	41	29	1681	1682	1189	697	696	985
6	99	70	9800	9801	6930	4059	4060	5741

Триплети Піфагора

Рівність $c^{2}=a^{2}+(a+1)^{2}=2a^{2}+2a+1$ вірно тільки при $2c^{2}=4a^{2}+4a+2$ , що перетворюється в $2P^{2}=H^{2}+1$ при підстановці $H=2a+1{\mbox{ and }}P=c$ . Тоді n-м рішенням є $a_{n}={\frac {H_{2n+1}-1}{2}}$ і $c_{n}={P_{2n+1}}.\,$

Таблиця вище показує, що з точністю до порядку $a_{n}$ і $b_{n}=a_{n}+1$ дорівнює $H_{n}H_{n+1}$ і $2P_{n}P_{n+1}$ , в той час як $c_{n}=H_{n+1}P_{n}+P_{n+1}H_{n}.$

Примітки

Наприклад, Селлерс (Sellers) в 2002 році показав, що кількість досконалих паросполучень в декартовому добутку шляхів і графу K₄-e може бути обчислена як добуток числа Пелля на відповідне число Фібоначчі
Про матричну формулу і її наслідках дивіться Ерколано (Ercolano) (1979), Кілік (Kilic) і Таскі (Tasci) (2005). Інші тотожності для чисел Пелля наведені Хорадамом (Horadam) (1971) і Бікнелл (Bicknell) (1975).
Це записано в Shulba Sutras. Дивіться, наприклад, Дутка (Dutka) (1986), який цитував Тібаута (Thibaut) (1875)
Дивись Кнорра (Knorr) (1976) з посиланням на п'яте століття, що відповідає твердженням Прокла, що числа були відкриті піфагорійцями. Для більш повного дослідження про більш пізніх знаннях греків про ці числа дивись Томпсона (Thompson) (1929), Ведова (Vedova) (1951), Ріденхоура (Ridenhour) (1986), Кнорра (Knorr) (1998), і Філепа (Filep) (1999).
Наприклад, в Державі Платона є посилання на «раціональний діаметр пчті», під яким Платон мав на увазі 7, чисельник наближення 7/5.
A History of Greek Mathematics: From Thales to Euclid - Sir Thomas Little Heath - Google Books. Процитовано 28 січня 2013.
Pethő (1992); Cohn (1996). Хоча числа Фібоначчі визначаються рекурентними формулами, дуже схожими на формули для чисел Пелля, Кон (Cohn) пише, що аналогічні результати для чисел Фібоначчі куди складніше довести. (Однак, вони були доведені у 2006 році Бугеадом (Bugeaud).)
Sesskin (1962).

Посилання

Bicknell, Marjorie (1975). A primer on the Pell sequence and related sequences. Fibonacci Quarterly 13 (4): 345–349. MR 0387173.
Cohn, J. H. E. (1996). Perfect Pell powers. Glasgow Mathematical Journal 38 (1): 19–20. MR 1373953. doi:10.1017/S0017089500031207.
Dutka, Jacques (1986). On square roots and their representations. Archive for History of Exact Sciences 36 (1): 21–39. MR 0863340. doi:10.1007/BF00357439.
Ercolano, Joseph (1979). Matrix generators of Pell sequences. Fibonacci Quarterly 17 (1): 71–77. MR 0525602.
Filep, László (1999). Pythagorean side and diagonal numbers. Acta Mathematica Academiae Paedagogiace Nyíregyháziensis 15: 1–7.
Horadam, A. F. (1971). Pell identities. Fibonacci Quarterly 9 (3): 245–252, 263. MR 0308029.
Kilic, Emrah; Tasci, Dursun (2005). The linear algebra of the Pell matrix. Boletín de la Sociedad Matemática Mexicana, Tercera Serie 11 (2): 163–174. MR 2207722.
Knorr, Wilbur (1976). Archimedes and the measurement of the circle: A new interpretation. Archive for History of Exact Sciences 15 (2): 115–140. MR 0497462. doi:10.1007/BF00348496.
Knorr, Wilbur (1998). "Rational diameters" and the discovery of incommensurability. American Mathematical Monthly 105 (5): 421–429. JSTOR 3109803. doi:10.2307/3109803.
Knuth, Donald E. (1994). Leaper graphs. The Mathematical Gazette 78 (483): 274–297. JSTOR 3620202. arXiv:math.CO/9411240. doi:10.2307/3620202.
Martin, Artemas (1875). Rational right angled triangles nearly isosceles. The Analyst 3 (2): 47–50. JSTOR 2635906. doi:10.2307/2635906.
Pethő, A. (1992). The Pell sequence contains only trivial perfect powers. Sets, graphs, and numbers (Budapest, 1991). Colloq. Math. Soc. János Bolyai, 60, North-Holland. с. 561–568. MR 1218218.
Ridenhour, J. R. (1986). Ladder approximations of irrational numbers. Mathematics Magazine 59 (2): 95–105. JSTOR 2690427. doi:10.2307/2690427.
Santana, S. F.; Diaz-Barrero, J. L. (2006). Some properties of sums involving Pell numbers. Missouri Journal of Mathematical Sciences 18 (1). Архів оригіналу за 8 травня 2007. Процитовано 25 травня 2015.
Sellers, James A. (2002). Domino tilings and products of Fibonacci and Pell numbers. Journal of Integer Sequences 5. MR 1919941.
Sesskin, Sam (1962). A "converse" to Fermat's last theorem?. Mathematics Magazine 35 (4): 215–217. JSTOR 2688551. doi:10.2307/2688551.
Thibaut, George (1875). On the Súlvasútras. Journal of the Royal Asiatic Society of Bengal 44: 227–275.
Thompson, D'Arcy Wentworth (1929). III.—Excess and defect: or the little more and the little less. Mind: New Series 38 (149): 43–55. JSTOR 2249223.
Vedova, G. C. (1951). Notes on Theon of Smyrna. American Mathematical Monthly 58 (10): 675–683. JSTOR 2307978. doi:10.2307/2307978.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Наприклад, Селлерс (Sellers) в 2002 році показав, що кількість досконалих паросполучень в декартовому добутку шляхів і графу K₄-e може бути обчислена як добуток числа Пелля на відповідне число Фібоначчі

[2] Про матричну формулу і її наслідках дивіться Ерколано (Ercolano) (1979), Кілік (Kilic) і Таскі (Tasci) (2005). Інші тотожності для чисел Пелля наведені Хорадамом (Horadam) (1971) і Бікнелл (Bicknell) (1975).

[3] Це записано в Shulba Sutras. Дивіться, наприклад, Дутка (Dutka) (1986), який цитував Тібаута (Thibaut) (1875)

[4] Дивись Кнорра (Knorr) (1976) з посиланням на п'яте століття, що відповідає твердженням Прокла, що числа були відкриті піфагорійцями. Для більш повного дослідження про більш пізніх знаннях греків про ці числа дивись Томпсона (Thompson) (1929), Ведова (Vedova) (1951), Ріденхоура (Ridenhour) (1986), Кнорра (Knorr) (1998), і Філепа (Filep) (1999).

[5] Наприклад, в Державі Платона є посилання на «раціональний діаметр пчті», під яким Платон мав на увазі 7, чисельник наближення 7/5.

[6] A History of Greek Mathematics: From Thales to Euclid - Sir Thomas Little Heath - Google Books. Процитовано 28 січня 2013.

[7] Pethő (1992); Cohn (1996). Хоча числа Фібоначчі визначаються рекурентними формулами, дуже схожими на формули для чисел Пелля, Кон (Cohn) пише, що аналогічні результати для чисел Фібоначчі куди складніше довести. (Однак, вони були доведені у 2006 році Бугеадом (Bugeaud).)

[8] Sesskin (1962).

Число Пелля

Числа Пелля

Наближення до квадратному кореню з двох

Прості і квадрати

Піфагорові трійки

Числа Пелля — Люка

Обчислення та зв'язки

Визначення

Наближення

H2 − 2P2 = ±1

Квадратні трикутні числа

Триплети Піфагора

Примітки

Посилання

H² − 2P² = ±1