Ізоедральне тіло

Багатогранник розмірності 3 та вище називається ізоедральним або гране-транзитивним, якщо всі його грані однакові. Точніше, всі грані мають бути не просто конгруентними, а мають бути транзитивними, тобто повинні прилягати в одній і тій самій орбіті симетрії. Іншими словами, для будь-яких граней A і B має існувати симетрія всього тіла (що складається з поворотів і відображень), яка відображає A в B. З цієї причини опуклі ізоедральні багатогранники мають форми правильних гральних кісточок[1].

Ізоедральні багатогранники називають ізоедрами. Їх можна описати конфігурацією їхніх граней. Ізоедральне тіло, що має правильні вершини, є також реберно-транзитивним тілом (ізотоксальним) і кажуть, що воно є квазіправильним двоїстим — деякі теоретики[хто?] вважають ці тіла істинно квазіправильними, оскільки вони зберігають ті самі симетрії.

Ізоедральний багатогранник має двоїстий багатогранник, який є вершинно-транзитивним (ізогональним). Тіла Каталана, біпіраміди і трапецоедри всі ізоедральні. Вони дуальні ізогональним архімедовим тілам, призмам і антипризмам відповідно. Правильні багатогранники, які або самодвоїсті, або двоїсті іншим платоновим тілам (правильним багатогранникам), вершинно-, реберно- і гране-транзитивні (ізогональні, ізотоксальні й ізоедральні). Ізоедральний і ізогональний одночасно багатогранник називають благородним багатогранником.

Приклади




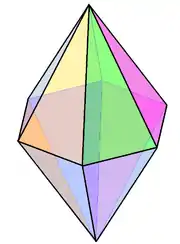Шестикутна біпіраміда V4.4.6 є прикладом неправильного ізоедрального багатогранника.



Ізоедральна каїрська п'ятикутна мозаїка, V3.3.4.3.4



Ромбододекаедральний стільник є прикладом ізоедрального (й ізохорного) стільника, що заповнює простір.

k-ізоедральне тіло

Багатогранник є k-ізоедральним, якщо він містить k граней у своїй фундаментальній області симетрії[2].

Аналогічно, k-ізоедральна мозаїка має k окремих орбіт симетрії (і може містити m граней різної форми для деякого m < k)[3].

Моноедральный (має грані одного виду) багатогранник або моноедральна мозаїка (m=1) мають конгруентні грані. r-едральный багатогранник або мозаїка має r типів граней (їх також називають діедральними, триедральними і так далі для m=2, 3, …)[4].

Кілька прикладів k-ізоедральних багатогранників і мозаїк з розфарбуванням граней в k симетричних позиціях:

3-ізоедральний 4-ізоедральний ізоедральний 2-ізоедральний
(2-едральні) багатогранники з правильними гранями Моноедральні багатогранники
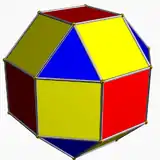
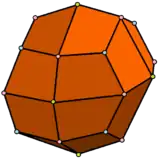
Ромбокубооктаедр має один тип трикутників і два типи квадратів Подовжений квадратний гіробікупол має один тип трикутників і три типи квадратів. Дельтоїдальний ікосітетраедр має один тип граней. Псевдодельтаедральний ікосаедр має 3 типи граней.
2-ізоедральна 4-ізоедральна ізоедральна 3-ізоедральна
(2-едральні) мозаїки з правильними гранями Моноедральні мозаїки
Піфагорова мозаїка має квадрати 2 розмірів. 3-однорідна мозаїка має 3 типи однакових трикутників і квадрати одного виду. Візерунок «Ялинка» має правильні грані одного типу. П'ятикутна мозаїка має 3 типи ідентичних неправильних п'ятикутних граней.

Пов'язані поняття

Комірко-транзитивне або ізохорне тіло є n-вимірним багатогранником (n>3) або стільником, які мають конгруентні і транзитивні, тобто такі, що переходять одна в іншу за допомогою симетрії,комірки.

Гране-транзитивне або ізотопне тіло (ізотоп) є n-вимірною фігурою або стільником з конгруентними і транзитивними фасетами ((n-1)-гранями). Двоїстий багатогранник ізотопа є ізогональним багатогранником. За визначенням, ця ізотопна властивість є спільною для двоїстих тіл однорідних багатогранників.

  • Ізотопна 2-вимірна фігура є ізотоксальною (реберно-транзитивною).
  • Ізотопне 3-вимірне тіло є ізоедральним (гране-транзитивним).
  • Ізотопне 4-вимірне тіло є ізохорним (комірко-транзитивним).

Див. також

Примітки
  1. McLean, 1990, с. 243–256.
  2. Socolar, 2007, с. 33–38.
  3. Kaplan, 2009, с. 35.
  4. Grünbaum, Shephard, 1987, с. 20, 23.

Література

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.